В курсе математики 7 класса вы научились вычислять значение степени с любым натуральным показателем.
Напомним, что степенью числа а с
натуральным показателем  (
(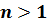 ),
называется выражение
),
называется выражение  ,
которое равно произведению
,
которое равно произведению 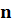 множителей,
каждый из которых равен
множителей,
каждый из которых равен 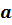 .
.

Степенью числа а с показателем единица является само число а. А вот при возведении в степень нуля всегда получаем нуль.

Также вам уже известны свойства степеней с натуральными показателями.
При умножении степеней с одинаковыми
основаниями основание остаётся прежним, а показатели степеней складываются.
Т.е. для любого числа 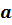 и
натуральных чисел
и
натуральных чисел 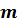 и
и
 верно
равенство:
верно
равенство:

При делении степеней с одинаковыми основаниями
основание остаётся прежним, а из показателя степени делимого вычитается
показатель степени делителя. Т.е. для любого числа 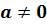 и
натуральных чисел
и
натуральных чисел 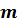 и
и
 ,
таких, что
,
таких, что  ,
справедливо равенство:
,
справедливо равенство:

Чтобы возвести в степень произведение, нужно
каждый множитель возвести в эту степень и результаты перемножить. Аналогично и
для частного. Т.е. для любых чисел 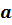 и
и
 и
натурального числа
и
натурального числа  верно
равенство:
верно
равенство:

При возведении степени в степень основание
оставляют прежним, а показатели степеней перемножают. Т.е. для любого числа 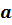 и
произвольных натуральных чисел
и
произвольных натуральных чисел 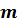 и
и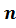 верно
равенство:
верно
равенство:

Заметим, что

Рассмотрим случай, когда показатель степени делимого меньше показателя степени делителя.

Такое соглашение принимается для степеней с любыми основаниями, отличными от нуля.
Определение:
Если 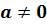 и
и
 –
целое отрицательное число, то верно равенство:
–
целое отрицательное число, то верно равенство:

Задание: заменить степень с целым отрицательным показателем дробью.
Решение:

Замечание: поскольку деление на
нуль невозможно, такие выражения, как 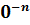 ,
не имеют смысла.
,
не имеют смысла.
Напомним, что при натуральном  выражение
выражение 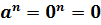 .
.
Задание: представьте числа в виде степени с основанием 3.
Решение:

Задание: найдите значения выражений.
Решение:
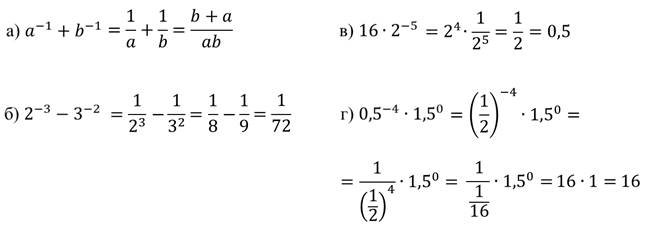
Итоги:


 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 20456
20456


