Правило умножения

Рассмотрим пример.

На турнире по шахматам встретились две команды. В первой команде было 4 игрока, а во второй – 3 игрока. Каждый игрок пожал руки всем игрокам из другой команды. Сколько было совершено рукопожатий?

Предположим, что каждая команда представляет собой множество. Игроки команды – элементы этого множества.

Можно считать, что каждое рукопожатие – это пара игроков. Тогда возникает множество пар. Выясним, сколько элементов в этом множестве.

Изобразим оба множества и рукопожатия с помощью графа. Синие вершины (их 4) – игроки из первой команды, зелёные вершины (их 3) – игроки из второй команды.

Каждая из 4 синих вершин будет связана с 3 зелёными вершинами, то есть из каждой синей вершины будет исходить ровно 3 ребра. Всего синих вершин 4, а значит, всего рёбер 4 умножить на 3, то есть 12.

Получается, что если имеется множество 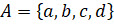 и множество , то можно составить множество пар:

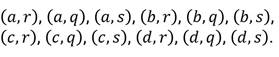
В каждой паре сначала записан какой-то элемент множества 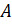, а потом – какой-то элемент множества 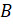. То есть пары упорядоченные. Всего таких пар в нашем примере 12.

Можно сделать вывод.

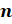Пусть в множестве  всего  элементов, а в множестве  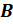всего 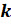 элементов. Тогда множество упорядоченных пар состоит из  элементов.

Это правило иногда применяется не столь прямо, как мы это сделали в задаче о шахматистах. В некоторых случаях его приходится немного видоизменять.

Пример. При встрече Саша, Вова, Антон, Костя и Максим обменялись рукопожатиями (каждый пожал руку другому по одному разу). Сколько рукопожатий было сделано?

Может показаться, что для решения этой задачи мы не можем воспользоваться правилом умножения, ведь у нас есть только одно множество. Но это не так. Правило умножения поможет и здесь.

Составим все возможные пары, используя множество из 5 человек дважды.

Пар будет 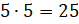. При этом мы посчитали пары, которые каждый образует сам с собой, то есть 5 пар будут лишними. Удалим их.

В результате останется 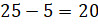 пар.

Также каждое рукопожатие было посчитано дважды. Например, получилось две пары: (Саша, Вова) и (Вова, Саша), а рукопожатие они сделали только одно. А значит, рукопожатий в 2 раза меньше, чем пар ().

Если при встрече рукопожатиями обменялись 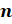 человек, а не 5, то рассуждая аналогичным образом, получим, что рукопожатий будет .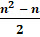

Давайте порассуждаем другим образом.

Каждый из 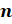 человек пожал руку каждому из  оставшихся. Тогда правило умножения даёт 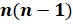 упорядоченных пар. Неупорядоченных пар в 2 раза меньше, то есть .

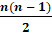Пример. Выясним, сколько диагоналей у восьмиугольника.

Диагональ многоугольника – это отрезок, который соединяет две несмежные вершины этого многоугольника.

Для произвольной вершины восьмиугольника найдётся 5 несмежных вершин (она сама и две соседние вершины не подходят). Следовательно, из этой вершины можно провести 5 диагоналей.

У восьмиугольника 8 вершин. Из каждой выходит по 5 диагоналей. Тогда всего получается  упорядоченных пар. При этом каждую диагональ мы посчитали 2 раза, а значит, всего диагоналей вдвое меньше ().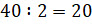

Запомните! Выражение, которое показывает, сколько диагоналей у 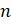-угольника, имеет вид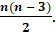

С помощью правила умножение можно перечислять не только пары, но тройки, четвёрки и т. д.

Пример. Сколько существует треугольников с вершинами в вершинах правильного пятиугольника?

Первую вершину треугольника можно выбрать пятью способами, вторую – четырьмя, третью – тремя.

При этом каждый треугольник посчитан 6 раз. Так, например, треугольник 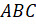 будет посчитан ещё как треугольник , , ,  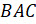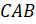и .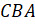

Пример. Сколько существует способов составить очередь из пяти человек?

Чтобы ответить на этот вопрос, воспользуемся правилом умножения.

На первой позиции будет любой из 5 человек. За ним можно поставить любого из 4 оставшихся. За ним – одного из 3 оставшихся. После него можно поставить одного из 2 оставшихся. В результате останется 1 человек, который займёт последнее место в очереди.

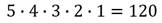
Применив правило умножения, получили, что общее число способов составить разные очереди из 5 человек равно 120.

В теории вероятностей правило умножения помогает перечислять события.

Например, общее число результатов двукратного бросания игрального кубика можно найти по правилу умножения ().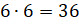

Если мы бросаем монету 3 раза, то может случиться один из 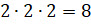 результатов, потому что каждый раз монета падает одной из двух сторон вверх.

Пример. Выясним, сколько различных результатов в случайном эксперименте, в котором игральный кубик бросают 4 раза.

Воспользуемся правилом умножения и получим, что при четырёхкратном бросании игрального кубика может случиться один из 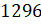 результатов ().

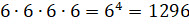Выполним задания.

Задание первое. В группе детского сада 10 мальчиков и 7 девочек. Сколько можно составить пар «мальчик – девочка»?

Решение. Пусть мальчики представляют собой множество, в котором 10 элементов, а девочки – множество, в котором 7 элементов. Тогда по правилу умножения можно составить 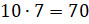 пар «мальчик – девочка».

Ответ: 70 пар.

Задание второе. В множес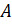тве  девять элементов, а в множестве 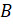 шесть элементов. Сколько можно составить пар вида 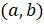, где , ?

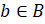Решение. Известно, что множество 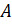 состоит из 9 элементов, а множество  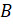– из 6 элементов. Тогда по правилу умножения можно составить  пары вида .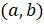

Ответ: 54 пары.

Задание третье. Сколько существует натуральных четырёхзначных чисел, которые составлены только из чётных цифр?

Решение. Чётными называются цифры: 0, 2, 4, 6 и 8.

Так как число не может начинаться цифрой 0, то первую цифру четырёхзначного числа можно выбрать только 4 способами. Вторую цифру можно выбрать 5 способами. Третью цифру можно выбрать 5 способами. Четвёртую цифру тоже можно выбрать 5 способами.

Тогда по правилу умножения получается, что существует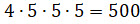 четырёхзначных чисел, которые составлены только из чётных цифр.

Ответ: 500 чисел.

До встречи на следующих занятиях!