Диаграммы Эйлера

Прежде чем приступить к рассмотрению новой темы, напомним, что пересечение множеств  и  – это множество, которое содержит элементы, принадлежащие и множеству , и множеству . Для обозначения пересечения множеств используют значок .

Объединение множеств  и  – это множество, содержащее все элементы, которые принадлежат хотя бы одному из множеств  и . Для обозначения объединения множеств используют значок .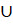

Важно помнить, что при объединении множеств общие элементы учитываются один раз.

Пример. Даны два числовых отрезка: 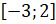 и .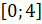

Найдём пересечение и объединение этих отрезков. Для этого на числовой прямой изобразим данные отрезки.

Пересечением отрезков является их общая часть, то есть отрезок .

Объединением отрезков является отрезок .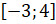

Изобразив на числовой прямой два числовых множества, мы смогли увидеть их пересечение и объединение.

А как быть со множествами, которые нельзя изобразить на числовой прямой?

Для изображения множеств произвольной природы удобно использовать диаграммы Эйлера.

Леонард Эйлер – выдающийся учёный, который жил в XVII веке. Он внёс огромный вклад в развитие физики, математики, астрономии и других наук. Его именем названы более 20 математических формул. В день 200-летия со дня рождения этого великого математика было издано на его родине, в Швейцарии, всё его наследие, которое состояло из 72 томов по 600 страниц.

Давайте изобразим множества  и  кругами.

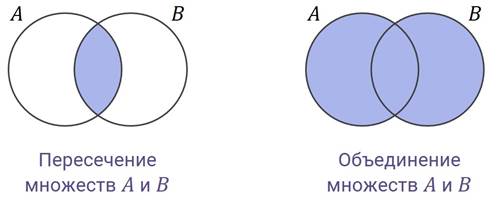
Мы изобразили множества кругами. Но это не обязательно. Для изображения можно использовать квадраты, треугольники и любые другие фигуры. Главное – правильно показать, как множества связаны друг с другом.

Диаграмма Эйлера – способ графического представления множеств и операций над ними с помощью геометрических фигур.

На диаграммах Эйлера можно показать не только пересечение и объединение множеств, но и наглядно представить включение одного множества в другое.

Пример. На рисунке изображена диаграмма Эйлера. Запишем все связи между множествами ,  и , которые только можно увидеть на данной диаграмме.

Нам неизвестно, что это за множества и каковы их элементы. Конечно, диаграмма Эйлера, изображённая на рисунке, даёт мало информации, но всё же кое-что сказать можно.

Множества  и  имеют непустое пересечение.

Множество  является подмножеством множества .

Множества  и  не пересекаются, то есть можно сказать, что их пересечение – пустое множество.

Это всё, что можно сказать, глядя на диаграмму Эйлера, изображённую на рисунке.

Иногда можно понять не только то, как связаны сами множества, но и как связано число элементов в одном множестве и число элементов во втором множестве.

Пример. В 8 классе 25 учеников. Из них 17 учеников являются читателями школьной библиотеки.

Пусть  – множество все учеников класса, а  – множество, состоящее из учеников класса, которые являются читателями школьной библиотеки.

Давайте выясним, сколько элементов содержит множество, которое является пересечением множеств  и , и множество, которое является объединением множеств  и .

Множество  является подмножеством множества , так как каждый из 17 учеников, являющихся читателями школьной библиотеки, учится в этом 8 классе.

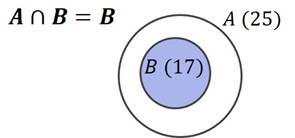
Чтобы найти пересечение множеств  и , нужно закрасить общую часть фигур. Общая часть совпадает с фигурой , поскольку она полностью лежит внутри фигуры . Значит, пересечением множеств  и  является множество . Поэтому пересечение содержит ровно 17 элементов, то есть столько, сколько содержит множество .

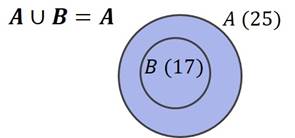
Чтобы найти объединение множеств  и , нужно закрасить обе фигуры. Получится фигура , поскольку фигура  лежит внутри. Значит, объединением множеств  и  является множество . Поэтому объединение содержит ровно 25 элементов, то есть столько, сколько содержит множество .

На этом примере с помощью диаграммы Эйлера мы проиллюстрировали важное свойство множеств, одно из которых содержит другое.

Если множество  является подмножеством множества , то пересечением множеств  и  является множество  и объединением множеств  и  является множество .

Выполним несколько заданий.

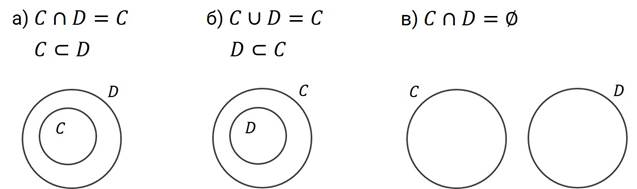
Задание первое. Изобразите на диаграмме Эйлера множества  и 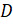, для которых выполняются данные соотношения.

Решение.

Чтобы выполнить это задание, воспользуемся сформулированным выше свойством.

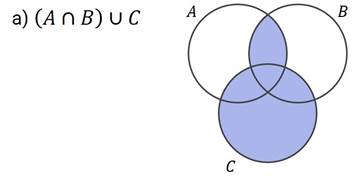
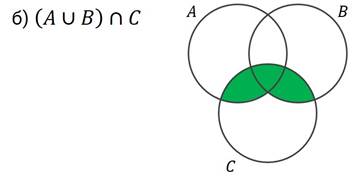
Задание второе. На рисунке изображена диаграмма Эйлера. Укажите на ней данные множества.

Решение.

До встречи на следующих занятиях!