Свойство биссектрисы угла

На этом уроке мы начнем знакомиться с точками, которые называют «замечательными точками треугольника» и узнаем, каким свойством обладают точки, лежащие на биссектрисе угла.

Напомню, что биссектриса угла – это луч, выходящий из вершины угла и делящий этот угол пополам (т.е. на два равных угла).

Для начала давайте вспомним, какие линии в треугольнике вам уже известны. Итак, это высоты, медианы и биссектрисы треугольника. Напомню, что:

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называют медианой треугольника.

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Рассмотрим свойства точки, лежащей на биссектрисе угла. Пусть есть угол BAC, причем АD биссектриса этого угла. Отметим на биссектрисе, например, точку M.

Теорема. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Доказательство.

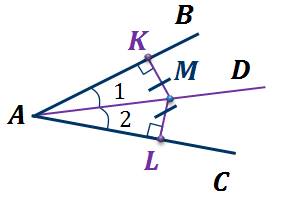
Докажем, что .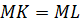

Рассмотрим 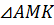 и .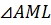

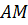 – общая сторона, 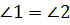 – по условию.

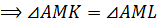 – по гипотенузе и острому углу.

.

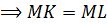Следовательно, точка, лежащая на биссектрисе угла, равноудалена от сторон этого угла.

Теорема доказана.

Обратная теорема. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Доказательство.

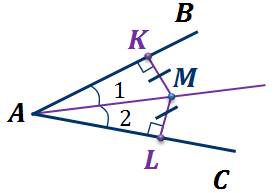
Докажем, что луч 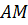 – биссектриса .

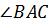Рассмотрим 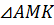 и .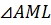

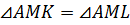 – по гипотенузе и катету, т.к. 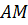 – общая сторона,

.

.

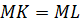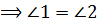Луч 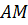 – биссектриса .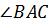

Теорема доказана.

Эти две теоремы: прямую и обратную можно объединить. Тогда справедлива теорема: Биссектриса неразвернутого угла есть геометрическое место точек, равноудаленных от сторон данного угла.

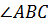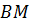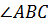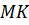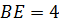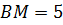Задача. Дан .  биссектриса . Найти длину , если  см,  см.

Решение.

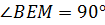
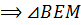  – прямоугольный.

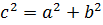
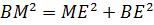
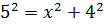
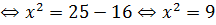
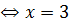   (см).

.

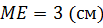
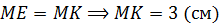Ответ: .

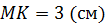А теперь перейдем к замечательным точкам треугольника. Замечательные точки треугольника — это точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.

Итак, первая замечательная точка треугольника.

Следствие. Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

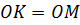 и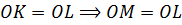

Точка 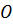 равноудалена от .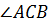

Точка 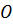 лежит на биссектрисе .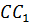

Следовательно, все три биссектрисы 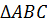 пересекаются в точке .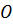

Что и требовалось доказать.

Задача. Биссектрисы 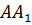 и 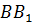 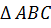 пересекаются в точке 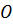.Найдите 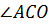 и 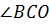, если .

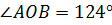Решение.

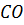 – биссектриса  ,

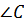
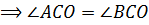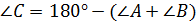
Рассмотрим .

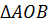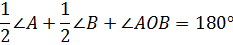
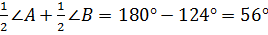
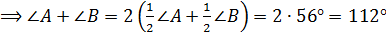
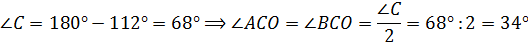
Ответ: .

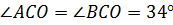Повторим главное:

На этом уроке мы рассмотрели, какими свойствами обладают точки биссектрисы неразвернутого угла. А именно, узнали, что каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. И каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе. А также узнали, что биссектрисы треугольника пересекаются в одной точке. И это есть первая замечательная точка треугольника.