Свойство серединного перпендикуляра к отрезку

На этом уроке мы узнаем, какими свойствами обладают точки, лежащие на серединном перпендикуляре к отрезку. А также познакомимся со второй замечательной точкой треугольника.

Мы с вами уже знакомы со свойствами точек, лежащих на биссектрисе угла. А точнее, мы знаем, что каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. И знаем, что биссектрисы треугольника пересекаются в одной точке. Эту точку называют замечательной точкой треугольника.

Перейдем к рассмотрению отрезка, его серединного перпендикуляра и свойства точки, которая лежит на серединном перпендикуляре.

Итак, пусть дан отрезок AB. Прямая l – есть серединный перпендикуляр к отрезку AB.

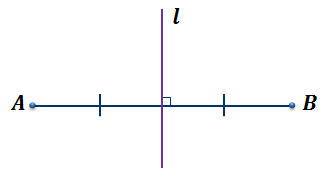
Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

Это означает, что наша прямая l проходит через середину отрезка AB и перпендикулярна ему.

Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Доказательство.

Докажем, что .

, т.к.  середина отрезка  по условию.

Рассмотрим  и .

,т.к.  – общий катет, катеты  равны по условию.

 равны по двум катетам.

.

Если точка лежит на серединном перпендикуляре к отрезку, то она равноудалена от концов отрезка.

Теорема доказана.

Обратная теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство.

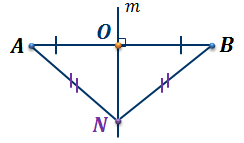
Докажем, что точка  лежит на прямой .

Рассмотрим .

 – равнобедренный,

т.к.   по условию.

Отрезок  – медиана .

 – высота

.

Значит, прямые  и  совпадают.

Точка  лежит на прямой .

Теорема доказана.

Прямую и обратную теоремы можно обобщить. Тогда справедлива теорема: Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.

Задача. Серединный перпендикуляр к стороне  равнобедренного   пересекает сторону  в точке . Найдите , если  см и периметр  см.

Решение.

 – по условию.

 (см).

Рассмотрим .

 – серединный перпендикуляр по условию.

Значит, .

  (см).

Ответ:  (см).

Как вы уже знаете, треугольник состоит из трех отрезков, значит, в нем можно провести три серединных перпендикуляра. Оказывается, эти перпендикуляры пересекаются в одной точке. Эту точку называют второй замечательной точкой треугольника.

Следствие. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

 и

Следовательно, все три серединных перпендикуляра ,  и  к сторонам  пересекаются в точке .

Таким образом, точка  – точка пересечения трех серединных перпендикуляров .

Что и требовалось доказать.

Повторим главное:

На этом уроке мы узнали, какими свойствами обладают точки, лежащие на серединном перпендикуляре к отрезку. А именно, каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. А также узнали, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. И это есть вторая замечательная точка треугольника.