Сегодня на уроке мы продолжим изучение темы замечательные точки треугольника и познакомимся с теоремой о пересечении высот треугольника.
На прошлых уроках мы доказали, что биссектрисы треугольника пересекаются в одной точке и серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке. До этого мы также доказали, что медианы треугольника пересекаются в одной точке. Оказывается, таким же свойством обладают и высоты треугольника.
Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство.
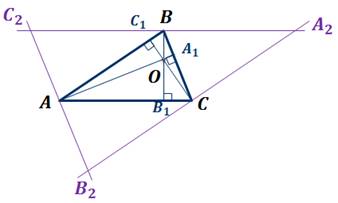
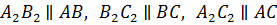
Рассмотрим 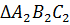 .
.
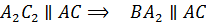
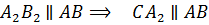
Значит, четырехугольник 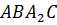 параллелограмм.
параллелограмм.
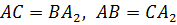
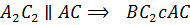
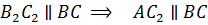
Значит, четырехугольник 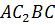 параллелограмм.
параллелограмм.
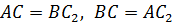
Точка 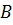 является серединой отрезка
является серединой отрезка 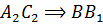 серединный перпендикуляр
серединный перпендикуляр 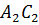 .
.
Точка 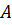 является серединой отрезка
является серединой отрезка 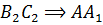 серединный перпендикуляр
серединный перпендикуляр 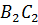 .
.
Точка 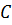 является серединой отрезка
является серединой отрезка 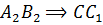 серединный перпендикуляр
серединный перпендикуляр 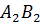 .
.
Значит, высоты 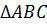 пересекаются
в одной точке, в точке
пересекаются
в одной точке, в точке 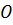 .
.
Что и требовалось доказать.
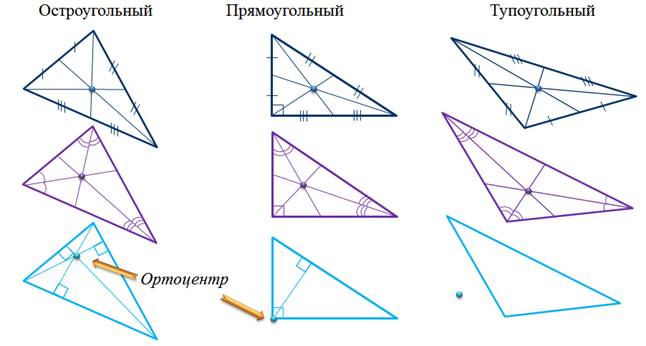
В любом треугольнике медианы и биссектрисы принадлежат самому треугольнику. Чего нельзя сказать о высотах треугольника. Три высоты треугольника всегда пересекаются в одной точке. Точку их пересечения называют ортоцентром треугольника. В остроугольном и прямоугольном треугольниках высоты принадлежат треугольнику. Их точка пересечения – ортоцентр – в остроугольном треугольнике находится внутри треугольника, в прямоугольном треугольнике находится в прямом угле. А вот в тупоугольном треугольнике точка пересечения высот – ортоцентр – находится вне треугольника.
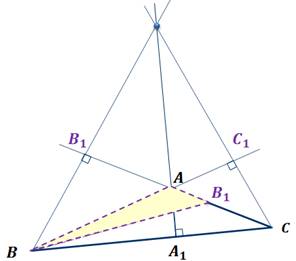
Рассмотрим тупоугольный 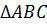 .
У него
.
У него 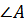 –
тупой,
–
тупой, 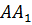 –
высота. Докажем, что точка
–
высота. Докажем, что точка 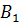 –
основание высоты
–
основание высоты 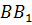 –
не принадлежит отрезку
–
не принадлежит отрезку 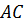 .
.
Доказательство.
Пусть точка 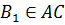 .
.
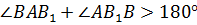 .
.
Что не может быть.
Точка пересечения тупоугольного треугольника лежит вне треугольника.
Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам треугольника и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.
Из истории замечательных точек треугольника. В четвертой книге "Начал" Евклид решает задачу: "Вписать круг в данный треугольник". Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга.
Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. В "Началах" не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром.
Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника. На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы "замечательными" или "особенными" точками треугольника.
Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – "геометрии треугольника" или "новой геометрии треугольника", одним из родоначальников которой стал Леонард Эйлер.
Повторим главное:
На этом уроке мы узнали, что высоты треугольника (или их продолжения) пересекаются в одной точке. Эту точку называют ортоцентром и она является замечательной точкой треугольника.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 51483
51483