Вписанная окружность

Сегодня на уроке мы узнаем, что такое вписанная окружность. Докажем, что в любой треугольник можно вписать окружность. А также покажем, что не во всякий четырехугольник можно вписать окружность.

Ранее мы с вами рассматривали касание прямой и окружности. Напомню, что если задана окружность с центром в точке O и радиусом r, и точка A – общая точка прямой и окружности, то такая точка единственная. Прямая p, которая проходит через точку касания, называется касательной. Радиус OA, проведенный в точку касания, перпендикулярен касательной p.

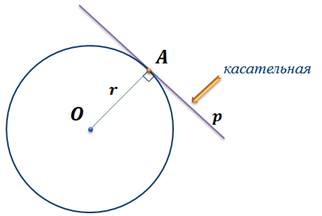
Напомним теорему: отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

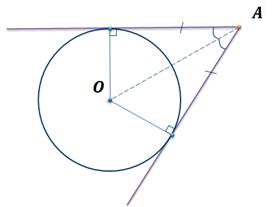
Значит, точка O– центр окружности – лежит на биссектрисе угла. Таким образом, имеем окружность, вписанную в угол.

Как мы уже знаем, многоугольник имеет несколько углов и несколько сторон.

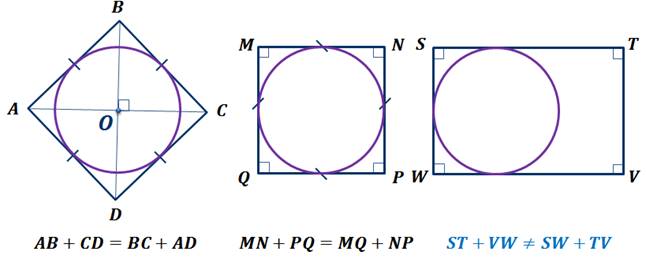
Определение. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

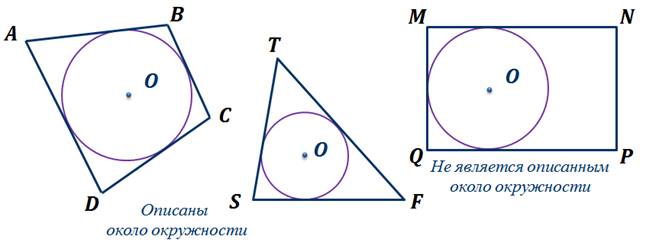
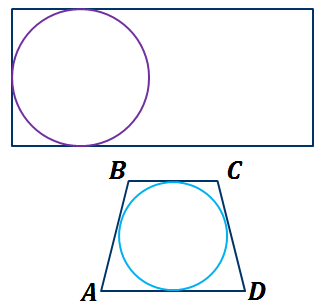
На рисунке вы видите четырехугольник ABCD, треугольник STF и четырехугольник MNPQ. Заметим, что четырехугольник ABCD и треугольник STF описаны около окружности с центрами в точке о. Что нельзя сказать о четырехугольнике MNPQ. Он не является описанным около окружности с центром O, так как его сторона NP не касается окружности.

Докажем теорему об окружности, вписанной в треугольник.

Теорема. В любой треугольник можно вписать окружность.

Доказательство.

.

.

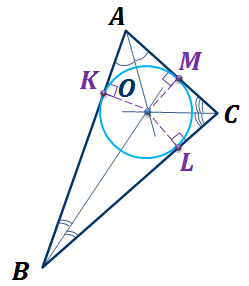
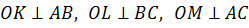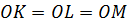Окружность касается всех трех сторон .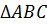

Окружность вписана в треугольник .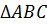

Теорема доказана.

Замечания.

1. В треугольник можно вписать только одну окружность.

Доказательство.

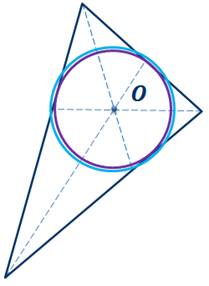
Допустим, в треугольник можно вписать две окружности.

Тогда центр второй окружности был бы равноудален от всех сторон треугольника и лежал бы на пересечении его биссектрис.

Но так как все биссектрисы пересекаются в единственной точке – в точке  – и радиус равен расстоянию от точки 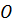 до сторон треугольника, то и вписанная в треугольник окружность единственная.

2. В отличие от треугольника не во всякий четырехугольник можно вписать окружность.

Доказательство.

Рассмотрим прямоугольник, у которого смежные стороны не равны.

В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон, но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.е. нельзя вписать окружность.

Что и требовалось доказать.

Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:

В любом описанном четырехугольнике суммы противоположных сторон равны.

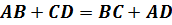
Доказательство.

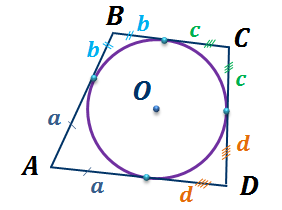
Рассмотрим четырехугольник .

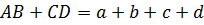
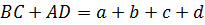
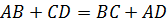
Следовательно, суммы противоположных сторон в описанном четырехугольнике равны.Что и требовалось доказать.

Верно и обратное утверждение:

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Доказательство.

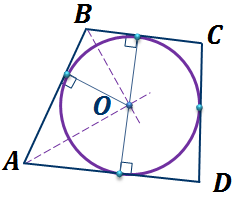
Рассмотрим выпуклый четырехугольник .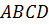

Пусть .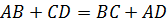

Докажем, что эта окружность касается также стороны 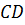. Будем доказывать от противного. Предположим, что это не так. Тогда возможны два случая.

1) Прямая 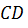не имеет общих точек с окружностью.

2) Прямая 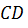пересекает окружность в двух точках, т.е. является секущей.

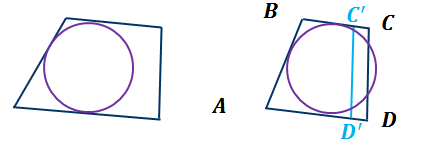
Так как 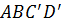 – описанный четырехугольник, то

.

,  

.

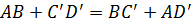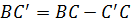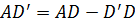
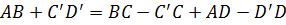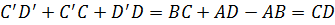
Значит, в четырехугольнике C’CDD’ одна сторона равна сумме трех других сторон. Этого же не может быть. А тогда наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны CD. Что и требовалось доказать.

Давайте ответим на вопрос: можно ли описать около окружности ромб, квадрат и прямоугольник. Почему?

Итак, рассмотрим ромб. У ромба все стороны равны, отсюда суммы его противоположных сторон равны. Значит, в ромб можно вписать окружность. Напомним, что диагонали ромба перпендикулярны и делят углы ромба пополам. Следовательно, каждая диагональ является биссектрисой соответствующего угла. А так как все четыре биссектрисы пересекаются в одной точке – в точке O – то точка O – центр вписанной окружности.

Следующая фигура квадрат. Квадрат – это частный случай ромба. У него все стороны равны, значит и суммы противоположных сторон также равны. Следовательно, в квадрат можно вписать окружность.

Что касается прямоугольника, то в него нельзя вписать окружность. Так как суммы его противоположных сторон не равны.

Задача. В равнобедренном треугольнике точка касания вписанной окружности делит боковую сторону на отрезки длино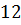й  см и 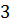 см, считая от основания. Найдите площадь треугольника.

Решение.

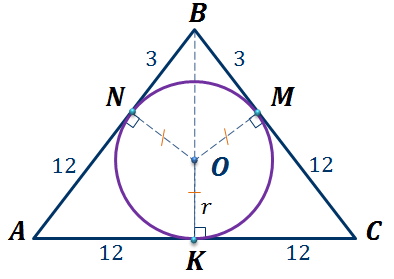
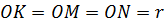
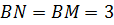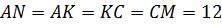 (см)

 (см)

Рассмотрим .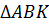

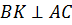
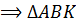   – прямоугольный.

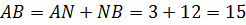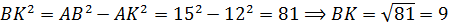 (см)

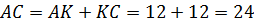 (см).

 (см)

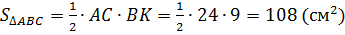
Ответ: .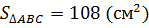

Повторим главное:

На этом уроке мы узнали, что если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник описанным около этого многоугольника. Доказали, что в любой треугольник можно вписать окружность. А вот, что касается четырехугольника, то не во всякий четырехугольник можно вписать окружность. И также узнали, что в любом описанном четырехугольнике суммы противоположных сторон равны.