На этом уроке мы узнаем, какую окружность называют описанной. Докажем, что около любого треугольника можно описать окружность. А также покажем, что около четырехугольника не всегда можно описать окружность.
Ранее мы с вами рассматривали вписанные углы. Напомню, что угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Если есть вписанный угол BAC и дуга BMC расположена внутри этого угла, то говорят, что вписанный угол BAC опирается на дугу BMC.
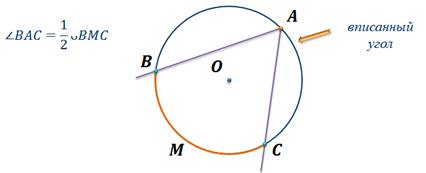
Также мы знаем, что вписанный угол измеряется половиной дуги, на которую он опирается.
Определение. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Докажем теорему об окружности, описанной около треугольника.
Теорема. Около любого треугольника можно описать окружность.
Доказательство.

 .
.
 .
.
Окружность проходит через все три вершины  .
.
Окружность описана около  .
.
Теорема доказана.
Замечания.
1. Около любого треугольника можно описать только одну окружность.
Доказательство.

Допустим, около треугольника можно описать две окружности.
Тогда центр каждой из них равноудален от его вершин и
поэтому совпадает с точкой  пересечения
серединных перпендикуляров, проведенных к сторонам треугольника.
пересечения
серединных перпендикуляров, проведенных к сторонам треугольника.
Радиус равен расстоянию от точки  до вершин треугольника.
до вершин треугольника.
Следовательно, эти окружности совпадают.
2. В отличие от треугольника около четырехугольника не всегда можно описать окружность.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
В любом вписанном четырехугольнике сумма
противоположных углов равна  .
.


Доказательство.
Рассмотрим четырехугольник  .
.
Докажем, что  .
.
 и
и  , то
, то 

Значит, сумма противоположных углов вписанного
четырехугольника равна  .
.

Что и требовалось доказать.
Аналогично доказывается, что
 . Это можно доказать и другим
путем. Мы знаем, что сумма внутренних углов выпуклого четырехугольника равна
360º. Как мы уже доказали выше, сумма
. Это можно доказать и другим
путем. Мы знаем, что сумма внутренних углов выпуклого четырехугольника равна
360º. Как мы уже доказали выше, сумма  . Значит, на сумму двух
других углов (угла B и угла D)
остается тоже 180º
. Значит, на сумму двух
других углов (угла B и угла D)
остается тоже 180º
Верно и обратное утверждение. Если сумма
противоположных углов четырехугольника равна  , то около него можно описать
окружность.
, то около него можно описать
окружность.
Доказательство
Рассмотрим четырехугольник  .
.
Пусть  .
.

Докажем, что эта окружность проходит также через
вершину  .
.
1) Вершина  может быть
расположена внутри круга.
может быть
расположена внутри круга.
2) Вершина  расположена
вне круга.
расположена
вне круга.

Тогда в четырехугольнике  будем иметь
будем иметь
 .
.
 .
.
 .
.
 .
.
Получили, что  .
.
Следовательно, вершина  лежит на окружности.
лежит на окружности.
Что и требовалось доказать.
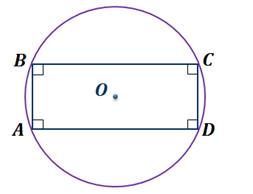
Как вы думаете, около прямоугольника можно описать окружность? Да! Ведь мы знаем, что у прямоугольника все углы равны девяноста градусам. А значит, сумма его противоположных углов составляет сто восемьдесят градусов. Следовательно, около прямоугольника можно описать окружность.
Задача. Найдите стороны остроугольного
равнобедренного треугольника, если высота, проведенная к его основанию, равна  см, а радиус
окружности, в которую он вписан
см, а радиус
окружности, в которую он вписан  см.
см.
Решение.

Пусть ABC – равнобедренный треугольник AB=BC, точка O – центр описанной около него окружности. BM высота треугольника ABC. Значит, она перпендикулярна стороне AC.


 (см)
(см)
 (см)
(см)
Рассмотрим  .
.

 – прямоугольный.
– прямоугольный.
 (см).
(см).
 (см).
(см).
 (см).
(см).

Ответ:  ,
,  (см).
(см).
Давайте рассмотрим рисунок к задаче и укажем, где находится центр окружности описанной около треугольника. Проведем серединные перпендикуляры к сторонам треугольника.

Напомним, что серединные перпендикуляры к сторонам треугольника, пересекаются в одной точке. Мы с вами уже говорили, что, так как треугольник ABC равнобедренный по условию, то высота BM является и его медианой, то есть она является и серединным перпендикуляром к стороне AC. Заметим, что точка пересечения серединных перпендикуляров совпала с центром окружности описанной около треугольника.
Следовательно, верно утверждение: перпендикуляры, восстановленные к серединам сторон треугольника (серединные перпендикуляры) пересекаются в одной точке, которая является центром описанной окружности.
Повторим главное:
На этом уроке мы узнали, что если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. Доказали, что около любого треугольника можно описать окружность. А вот, что около четырехугольника не всегда можно описать окружность. И также узнали, что в любом вписанном четырехугольнике сумма противоположных углов равна 180º.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 14582
14582

