С прошлых уроков вы уже знакомы с понятиями дуга, полуокружность, центральный угол (это угол с вершиной в центре окружности). Вы уже знаете, что градусная мера дуги, не большей полуокружности, равна градусной мере центрального угла, который опирается на данную дугу.
Сегодня мы будем говорить о вписанном угле.
Это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
В данном случае изображён вписанный угол ABC, вершина B лежит на окружности. Дуга AC находиться внутри данного вписанного угла. Говорят, что угол ABC опирается на дугу AC.
Запишем теорему о вписанном угле.
Теорема 1. Вписанный угол измеряется половиной дуги, на которую он опирается.
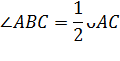
Доказательство.
Рассмотрим три случая расположения луча BO относительно угла ABC.

Что и требовалось доказать.
Запишем следствия из данной теоремы.
Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
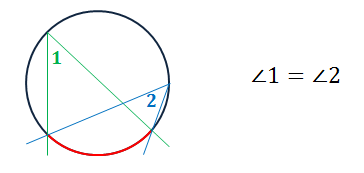
Следствие 2. Вписанный
угол, опирающийся на полуокружность прямой.
прямой.

Задача. По данным
рисунка найдите 
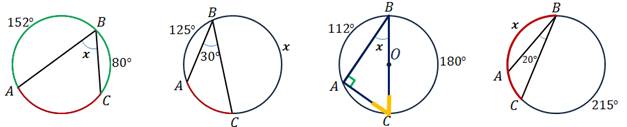
Решение
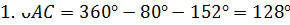


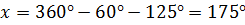
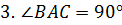
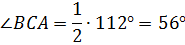


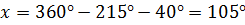
Задача. Найдите
величину 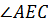 .
.
Если известно, что хорды 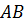 и
CD окружности
пересекаются в точке
и
CD окружности
пересекаются в точке  ,
,
и градусная мера 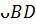 равна
равна
 ,
а
,
а  —
—
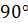 .
.
Решение.

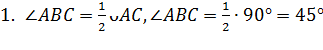

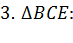

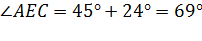
Ответ:  .
.
А сейчас запишем ещё одну теорему.
Теорема 2. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
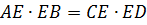
Доказательство.







Что и требовалось доказать.
Задача. Из двух пересекающихся хорд одна разделилась на части в 48 см и 3 см,
а другая — пополам. Найдите длину второй хорды.
Решение.

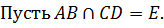





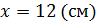

Ответ:  .
.
Задача. Из точки, данной на окружности, проведены диаметр и хорда, равная радиусу. Найдите угол между ними.
Решение.

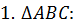
 (
(


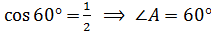
Ответ:  .
.
Задача. Найти острый угол между двумя секущими, проведёнными из точки, лежащей вне окружности, если дуги, заключённые между секущими,
равны 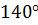 и
и
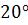 .
.
Решение.






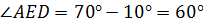
Ответ:  .
.
Подведём итоги нашего урока.
Сегодня мы познакомились с понятием вписанного угла. Научились находить его величину как половину градусной меры дуги, на которую он опирается.
Мы выяснили, что:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
А вписанный угол, опирающийся на полуокружность — прямой.
А также сегодня вы узнали, что если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 41690
41690

