Градусная мера дуги окружности

Рассмотрим окружность. Отметим на ней две точки А и B. Эти точки разделяют окружность на две дуги.

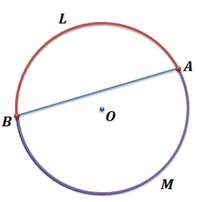
Возникает вопрос, а как узнать про какую дугу говорить? Ведь и одна и вторая дуги стягивается хордой АB. Именно для того, чтобы различать дуги, берутся дополнительные точки на этих дугах. Дуги обозначаются специальным знаком и тремя заглавными буквами. Запишем дуги, которые у нас получились: ᴗ, ᴗ. Иногда дуга может обозначаться двумя буквами, но только в том случае, когда точно ясно о какой дуге идет речь. Например, если дуга стягивается диаметром ᴗ. Такая дуга носит особое название – полуокружность.

Давайте введем еще одно определение. Угол с вершиной в центре этой окружности называется центральным углом.

По рисунку видно, что центральный угол может быть любым: как меньше развернутого, так и больше развернутого. Давайте попробуем на рисунке указать центральные углы.

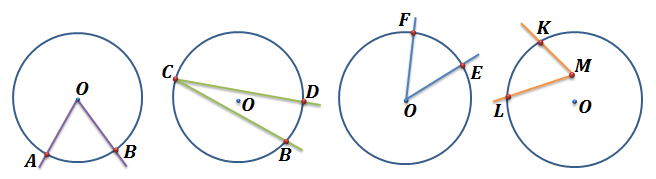
Центральными углами будут углы AOB и EOF. Пусть стороны центрального угла окружности пересекают ее в точках А и B. Центральному углу AOB соответствуют две дуги с концами А и B. Если этот угол развернутый, то ему соответствуют две полуокружности. Если угол не развёрнутый, то говорят, что дуга АB, расположенная внутри этого угла, меньше полуокружности. Про другую дугу говорят, что она больше полуокружности.

Мы помним, что длина окружности вычисляется по формуле . И измеряется длина только в единицах измерения длины. А дуга может измеряться, как в единицах измерения длины, так и в градусах.

, , ; , , ,

Если дуга AB окружности меньше полуокружности или является полуокружностью, то ее градусная мера равна градусной мере центрального угла АОB. Мы знаем, что градусная мера круга равна 360º, поэтому если дуга AB больше полуокружности, то ее градусная мера .

Решим задачу. Найти градусную меру дуг по рисункам.

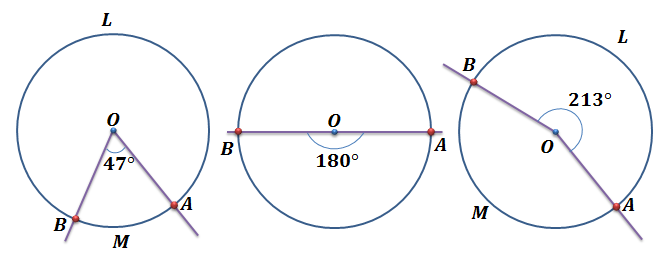
На первом рисунке дуга BMA меньше полуокружности:  .

На втором рисунке изображены две полуокружности, их градусные меры равны .

На третьем рисунке дуга BMA меньше полуокружности и, значит, ее градусная мера равна ,

Решим несколько задач.

Задача. Начертить окружность с центром  и отметить на ней точку . Построить хорду  так, чтобы:

а) ,          б) ,       в) ,      г)

Решение.

Построим окружность, с центром в точке О. Отметим на окружности точку А. Соединим точки А и О.

Возьмем циркуль и померяем получившийся отрезок ОА. И таким же радиусом проведем окружность, центром которой будет точка А. Эта окружность пересечет исходную окружность в двух точках. Обозначим одну из нах буквой B. Рассмотрим треугольник AOB. Поскольку точка B лежит на окружности, то ОА и ОB равны как радиусы, поскольку из точки А мы проводили окружность с таким же радиусом, то ОА равно AB. Таким образом, треугольник АОВ – равносторонний. Углы равностороннего треугольника равны по 60 градусов, то есть угол АОВ =60º.

Таким образом, мы построили хорду АB так, чтобы угол АОB был равен 60 º.

Теперь давайте построим хорду АБ так, чтобы угол АОB=  90º.

Проведем через точки А и О диаметр окружности. Из точки О проведем перпендикуляр к построенному диаметру, полученный перпендикуляр пересекает окружность в двух точках. Обозначим одну из них за B. Хорда АB и будет искомая.

Теперь давайте построим хорду АB так, чтобы угол АОB=120º.

 Для этого проведем через точки О и А диаметр окружности. Он делит окружность на две полуокружности, градусная мера которых равна 180º.

Построим хорду АB, так, чтобы один из центральных углов был равен 60º.

Обозначим вторую точку диаметра C и проведем окружность с радиусом равным радиусу исходной окружности и центром в точке C. Обозначим одну из точек пересечения окружностей за B и получим, что угол COB= 60º, (мы уже выяснили почему), тогда угол АОB= 180-60= 120º. То есть хорда АB – искомая.

Теперь нам надо построить хорду Аб так, чтобы угол АОБ был бы равен ста восьмидесяти градусам. Такой хордой, будет диаметр проведенный через точку А.

Обозначим второй конец диаметра буквой Б и получим искомую хорду.

Задача. Хорды  и  окружности с центром  равны. Доказать, что две дуги с концами  и  соответственно равны двум дугам с концами  и . Найти градусные меры дуг с концами  и , если .

Решение. Выполним чертеж.

 и

 и  по условию

Ответ:.

Задача. На полуокружности  взяты точки  и  так, что , . Найдите хорду , если .

Решение. Выполним чертеж.

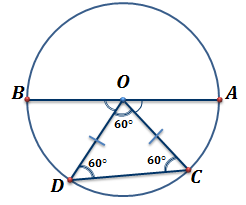
− равносторонний

 (см)

Ответ: см.

Итак, давайте повторим главное: Дуга – часть окружности. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.

Угол с вершиной в центре окружности называется центральным углом этой окружности. Если дуга АB окружности меньше полуокружности или является полуокружностью, то ее градусная мера равна градусной мере центрального угла АОB. Мы знаем, что градусная мера круга равна 360º, поэтому если дуга AB больше полуокружности, то ее градусная мера считается равной .