Давайте вспомним, как могут располагаться окружность и прямая в зависимости от отношения расстояния от центра окружности до прямой и радиуса окружности.
Напомним, что если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Сегодня мы особо рассмотрим случай, когда прямая и окружность имеют одну общую точку. Такая прямая называется касательной к окружности. А общая точка окружности и прямой называется точкой касания прямой и окружности.
Давайте, на рисунке укажем касательные к окружности и назовем точки касания.
Здесь касательными к окружности будут прямые b и d, точками касания будут точки C и F.

Теперь давайте из центра окружности проведем радиусы к точкам касания. По рисунку можно предположить, что радиусы, проведенные к точке касания будут перпендикулярны касательной.
Давайте попробуем доказать или опровергнуть это утверждение.

Пусть прямая p – касательная к окружности с центром в точке О и точка А – точка касания.
Предположим, что касательная p не перпендикулярна радиусу ОА. Тогда радиус ОА – наклонная к прямой p. Опустим из точки О перпендикуляр на прямую p. Поскольку перпендикуляр, проведенный из точки меньше любой наклонной, проведенной из этой же точки, то получаем, что расстояние от точки О до прямой p меньше радиуса, то есть прямая и окружность пересекаются в двух точках. Но тогда прямая p – секущая, а по условию, она – касательная.
Таким образом, предположение о том, что касательная не перпендикулярна радиусу, проведенному к точке касания, не подтвердилось.
То есть мы доказали свойство касательной к окружности. Сформулируем ее:
Теорема (свойство касательной). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Задача. Радиус  окружности с центром
окружности с центром  делит хорду
делит хорду  пополам. Доказать, что касательная, проведенная через
точку
пополам. Доказать, что касательная, проведенная через
точку  , параллельна хорде
, параллельна хорде  .
.
Доказательство.

 равнобедренный
равнобедренный
 медиана и высота
медиана и высота
Построим окружность, проведем хорду АB, проведем радиус ОК, который делит хорду АB пополам. Проведем касательную к окружности в точке К.
Проведем радиусы ОА и ОB и рассмотрим равнобедренный треугольник AOB. Поскольку ОК делит AB пополам, то часть этого отрезка OH будет являться медианой и высотой, то есть OH перпендикулярно AB. По свойству касательной, касательная, проведенная в точке К будет перпендикулярна ОК. Таким образом, мы получили две прямые, которые перпендикулярны радиусу ОК.
 и
и 
Что и требовалось доказать.
Теперь давайте рассмотрим две касательные к окружности с центром О, проходящие через точку А и касающиеся окружности в точках B и C. Отрезки AB и АС называются отрезками касательных, проведенными из точки А. Эти отрезки обладают следующим свойством:
Теорема. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Доказательство.

 и
и 
 ,
,  – общая,
– общая,  – как радиусы
– как радиусы 
Следовательно,  ,
, 
Что и требовалось доказать.
Это свойство запомнить не сложно, достаточно вспомнить героя сказок – Буратино. Его круглое личико мы примем за окружность. А стороны его колпачка – за касательные, проведенные из одной точки. Очевидно, что стороны колпачка равны, и если мы проведем линию из центра колпачка вертикально вниз, то углы тоже будут равны.
Задача. Через концы хорды  , равной радиусу окружности, проведены две
касательные, пересекающиеся в точке
, равной радиусу окружности, проведены две
касательные, пересекающиеся в точке  . Найдите
. Найдите  .
.
Решение. Выполним чертеж.

 − равносторонний
− равносторонний

 (по свойству отрезков касательной)
(по свойству отрезков касательной)
 (по свойству касательной)
(по свойству касательной)

 (по свойству углов равнобедренного треугольника)
(по свойству углов равнобедренного треугольника)

Ответ: 
Теперь, давайте попробуем сформулировать и доказать признак касательной.
Теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Доказательство.

По условию теоремы, данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой. А значит, он является расстоянием от центра окружности до прямой. То есть радиус окружности и расстояние до прямой равны, а, значит, окружность с прямой имеют одну общую точку. То есть, прямая является касательной к окружности, что и требовалось доказать.
Задача. Через данную точку  окружности с центром
окружности с центром  провести касательную к этой окружности.
провести касательную к этой окружности.
Решение.
Построим прямую ОА. Через точку А проведем прямую p перпендикулярно прямой ОА. По признаку касательной, эта прямая будет касательной к окружности в точке А.

Задача. К окружности с радиусом  проведена касательная из точки
проведена касательная из точки  , удаленной от центра на расстояние, равное
, удаленной от центра на расстояние, равное  . Найти длину отрезка касательной от точки
. Найти длину отрезка касательной от точки  до точки касания.
до точки касания.
Решение. Сделаем чертеж.

Рассмотрим треугольник АОB.  (по свойству
касательной)
(по свойству
касательной)  (по теореме Пифагора)
(по теореме Пифагора)
 ;
; 
Ответ: 
Задача. Доказать, что касательные к окружности, проведенные через концы диаметра, параллельны.
Решение. Выполним чертеж.
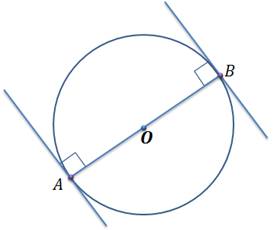
По свойству касательных, углы между диаметром и
касательными равны  .
.
Значит, по признаку параллельности прямых, получаем, что касательные параллельны.
Задача. Отрезки  и
и  являются отрезками касательных к окружности с центром
являются отрезками касательных к окружности с центром
 , проведенными из точки
, проведенными из точки  . Найти
. Найти  , если середина отрезка
, если середина отрезка  лежит на окружности.
лежит на окружности.
Решение. Выполним чертеж.

 ,
,  (по свойству касательных)
(по свойству касательных)
Рассмотрим треугольник ОАМ. По свойству касательной – это прямоугольный треугольник с катетом равным радиусу и гипотенузой, равной двум радиусам.
 и
и  (по свойству отрезков касательных)
(по свойству отрезков касательных) 

Ответ:
Давайте повторим главное:
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойство касательной к окружности. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Еще раз сформулируем свойство отрезков касательных, проведенных из одной точки. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Сформулируем признак касательной.
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

 Получите свидетельство
Получите свидетельство Вход
Вход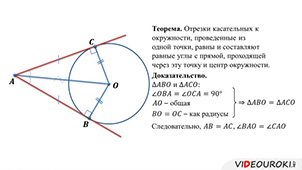



 0
0 16025
16025

