Прежде чем приступить к новой теме, давайте вспомним, что такое окружность и вспомним основные элементы окружности.
Напомню, что окружностью называется геометрическая фигура, состоящая из всех точек, равноудаленных от точки О, которую называют центром окружности. Отрезок, соединяющий центр окружности с любой точкой на окружности, называется радиусом. Отрезок, соединяющий две любые точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром и равна двум радиусам.
Сегодня мы выясним, сколько общих точек могут иметь окружность и прямая. Если прямая p проходит через центр окружности, то, очевидно, она имеет с окружностью две общие точки.
Теперь давайте рассмотрим случай, когда прямая p не проходит через центр окружности. Опустим на прямую перпендикуляр из центра окружности и обозначим его буквой d. Длина этого перпендикуляра – расстояние от центра окружности до данной прямой p.
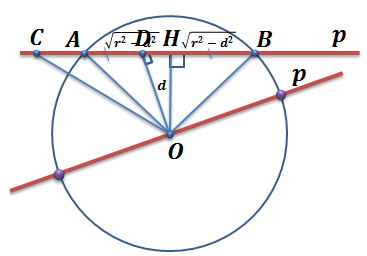
Теперь давайте попробуем определить взаимное расположение прямой и окружности в зависимости от соотношения d и радиуса окружности. Возможны три случая:
Первый случай. 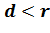


Получим, что ОА и ОB равны радиусу окружности, то есть точки А и B лежат на окружности. А, значит, они являются общими точками прямой p и окружности.
А может быть есть еще общие точки, у прямой и окружности? Допустим, что, действительно, есть еще одна общая точка C. Тогда медиана ОD равнобедренного треугольника OBC, проведенная к основанию AC, является высотой, то есть перпендикулярна прямой p. Поскольку середина отрезка AB – точка H не совпадает с серединой отрезка AC – точкой D, значит, отрезки ОD и ОH не совпадают. Получается, что из точки О проведены два перпендикуляра к прямой p, а такого быть не может.
То есть доказали, что если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки. В таком случае, прямая называется секущей по отношению к окружности.
Рассмотрим второй случай.
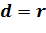
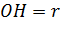
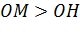
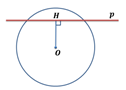
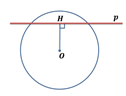
В этом случае, длина перпендикуляра ОH=r, то есть точка H лежит на окружности. Больше общих точек у прямой и окружности нет.

Докажем это. Возьмем на прямой точку М. В любом случае ОМ будет больше OH, следовательно, точка М не будет лежать на окружности.
Таким образом, если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. В таком случае, прямая называется касательной к окружности.
Теперь, давайте, рассмотрим третий случай.
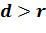
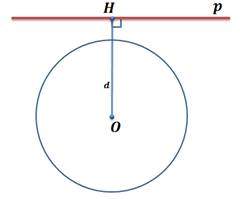
В
этом случае,  , то есть, окружность и прямая не имеют общих точек. Можно сказать, что
если расстояние от центра окружности до прямой больше радиуса окружности, то
прямая и окружность не имеют общих точек.
, то есть, окружность и прямая не имеют общих точек. Можно сказать, что
если расстояние от центра окружности до прямой больше радиуса окружности, то
прямая и окружность не имеют общих точек.
Задача. Определить взаимное расположение прямой и окружности, если:
а) 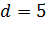 ,
, 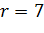 ; б)
; б) 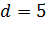 ,
, 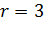 ; в)
; в) 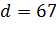 ,
, 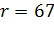 ;
;
Решение.
а)
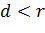 , прямая является секущей для окружности и они
имеют две общие точки
, прямая является секущей для окружности и они
имеют две общие точки
б)
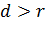 , прямая и окружность не пересекаются
, прямая и окружность не пересекаются
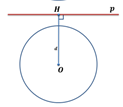
в)
 , прямая и окружность имеют одну общую точку
, прямая и окружность имеют одну общую точку

Задача.
Диаметр окружности равен 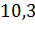 см
см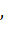 а расстояние от центра окружности до прямой равно:
а расстояние от центра окружности до прямой равно: 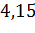 см
см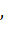
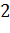 дм
дм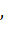
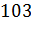 мм
мм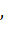
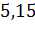 см
см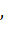
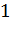 дм
дм 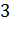 см.
см.
Решение.
Найдем радиус окружности.
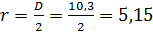 см
см
Теперь сравним получившийся радиус с расстоянием от центра окружности до прямой. Не забудем все перевести в одни единицы измерения.
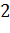 дм
дм 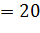 см
см 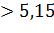
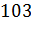 мм
мм 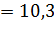 см
см 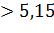
 дм
дм 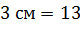 см
см 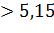
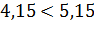
Получим, что с прямой, расстояние до которой равно четырем целым пятнадцать сотых сантиметра, окружность имеет две общие точки.
С прямой, расстояние до которой равно двум дециметрам или двадцати сантиметрам, окружность не имеет общих точек.
С прямой, расстояние до которой равно сто три миллиметра, окружность не имеет общих точек.

Задача.
Даны окружность с центром в точке 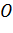 и точка
и точка 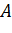 . Где находится точка
. Где находится точка 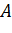 , если
, если 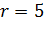 см, а длина отрезка
см, а длина отрезка 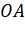 равна:
равна: 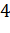 см,
см, 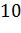 см,
см, 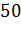 мм.
мм.
Решение. Для определения места положения точки А, сравним длину отрезка ОА с радиусом окружности.
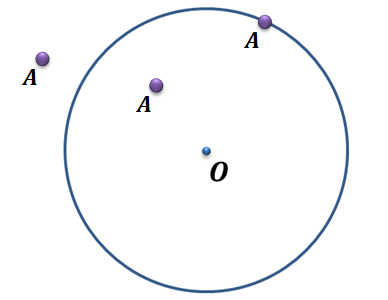
Получим,
что в случае, когда длина отрезка равна 4 сантиметрам, точка А лежит внутри
окружности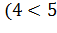 ), в случае, когда ОА равно 10 сантиметрам, точка
А лежит вне окружности (
), в случае, когда ОА равно 10 сантиметрам, точка
А лежит вне окружности (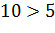 ). В случае, когда ОА равно 50 миллиметрам или, что тоже самое, 5
сантиметрам, точка А лежит на окружности(
). В случае, когда ОА равно 50 миллиметрам или, что тоже самое, 5
сантиметрам, точка А лежит на окружности(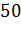 мм
мм 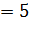 см)
см)
Итак, сегодня на уроке мы рассмотрели три случая взаимного расположения прямой и окружности, в зависимости от соотношения расстояния от центра окружности до прямой и радиуса окружности. Повторим их.
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 16763
16763


