А.Ж. Дюсекеева
учитель ГУ лицея, г. Аксу
УЧЕБНЫЙ ЛИСТ
Глава «Квадратные уравнения».
В результате изучения тем нужно
| Знать: - определение квадратного уравнения; - способы решения квадратных уравнений; - формулы для нахождения корней квадратных уравнений; - алгоритм решения дробно-рациональных и биквадратных уравнений; - теорему Виета. | Уметь: - находить корни квадратного уравнения; решать дробно-рациональные и биквадратные уравнения; - составлять уравнение по заданным его корням. |
ЛИТЕРАТУРА:
1. А. Абылкасымова,Алгебра учебник 8 класса общеобразовательной школы . Алматы «Мектеп», 2012г
2. С.К.Тулеубаева ,В.Е.Корчевский Алгебра 8 класс. Сборник задач. Алматы «Мектеп», 2012г.
3.К.Базаров, Алгебра 8 класс. Дидактические материалы. г Алматы: «Мектеп», 2004г.
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях, заполнять рейтинговый лист темы.
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому, кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
Теория без практики мертва или бесплодна
Практика без теории невозможна или пагубна
Для теории нужны знания, для практики сверх того, и умения.
А.Н.Крылов
.
I. Полные и неполные квадратные уравнения
Прочитай текст:
Уравнение вида ах 2 + вх + с = 0, где х - переменная, , а, в и с - некоторые действительные числа, если а≠ 0, называется уравнением второй степени.
Если а = 0, то уравнение примет вид BX + C = 0 и будет уравнением первой степени .
Неполные квадратные уравнения:
Если в = 0, то уравнение примет вид ах2 + с = 0
Если с = 0, то уравнение примет вид ах2 + вх = 0
Если с = 0, в=0, то уравнение примет вид ах2 = 0
Д= в2-4ас Если D
Если D = 0, то корни совпадают и равны х1/2=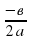
Если D 0,то,извлекая корень, получим х1/2=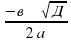
Это и есть формула для решения квадратного уравнения.
№1. Какой из данных уравнений является а) квадратным уравнением б) приведенным квадратным уравнением : по (1б)
1) 2х+3=0; 2) х2-19х=0; 3) х3-х2+5=0; 4)3х3-0,4х2-х=0; 5) -3х-х2+7=0
№2. Решить уравнения а) :3х2+4х-7=0
б) 9х2-4=0 в) 2=7х2+2 г) 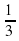 х2+
х2+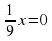 е)2х2-2х+0,5=0 к)
е)2х2-2х+0,5=0 к) 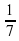 а=а2+4 (по 2б.)
а=а2+4 (по 2б.)
Алгоритм решения приведенного квадратного уравнения путем выделения квадрата двучлена:
Х2+px+c=0
1) х2+2px+q=0
2) х2+2px+p2=p2-q
3) (x+p)2=p2-q
4) x+p = 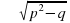 , если p2-q
, если p2-q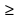 0
0
5) х = -p 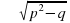
№3. Решить уравнение: Х2-6х+8=0 (2б.)
Определение. Биквадратное уравнение — это любое уравнение вида:
ax4 + bx2 + c = 0, где a, b, c — любые числа, причем a ≠ 0.
Примеры. Вот несколько биквадратных уравнений: x4 − 5x2 + 6 = 0; 3x4 − 2x2 + 1 = 0;
x4 − 1 = 0.
Как решать биквадратные уравнения: общая схема
Биквадратные уравнения легко сводятся к обычным квадратным с помощью замены переменной. Поэтому алгоритм выглядит следующим образом:
Ввести новую переменную: t = x2
Подставить эту переменную в исходное уравнение. Мы получим обычное квадратное уравнение, которое решается через дискриминант: ax4 + bx2 + c = 0 ⇒ at2 + bt + c = 0;
Решаем полученное квадратное уравнение. Получим корни t1 и t2;
Подставляем эти корни в формулу замены переменной: x2 = t1и x2 = t2;
Решаем эти два уравнения — получаем искомые корни биквадратного уравнения.
№4.Решите уравнение:
а) x4 − 13x2 + 36 = 0 ( 3б.)
II. Теорема Виета. Уравнения, содержащие модуль.
Сумма корней приведенного квадратного трехчлена x2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q,
т. е.x1 + x2 = – p и x1 x2 = q Если а=1 (приведенная форма x2 + px + q = 0), то (теорема Виета)
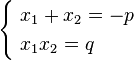 .
.
№1. Решите уравнение с помощью теоремы Виета: а) х 2 + 2 х - 3 = 0. (2б)
б) х 2 + 6 х + 9 = 0. (2б)
Обратная Теорема Виета. Если числа x1 и x2 удовлетворяют соотношениям x1 + x2 = – p и x1 x2= q, то они удовлетворяют квадратному уравнению x2 + px + q = 0.
№2. Составить квадратное уравнение, если х1= 2+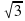 и х2 =2-
и х2 =2-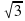 (2б.)
(2б.)
Самый распространённый, а иногда и единственно возможный метод решения уравнений с модулем – раскрытие модуля согласно определению:
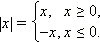
№3. Решить уравнение: 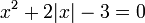 . 4(б.)
. 4(б.)
III. Дробно-рациональные уравнения.
Если в рациональном уравнении есть деление на выражение, содержащее переменную (x), то уравнение называется дробно-рациональным.
Дробные рациональные уравнения обычно решаются следующим образом:
| 1) находят общий знаменатель дробей и умножают на него обе части уравнения; 2) решают получившееся целое уравнение; 3) исключают из его корней те, которые обращают в ноль общий знаменатель дробей, т.е. определяют посторонние корни |
а) 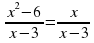 (2б.) б)
(2б.) б) 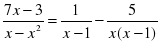 (3б.)
(3б.)
в) 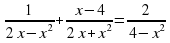 (4б.)
(4б.)
Итого: 38 баллов
«5» - 36-38б. «4» - 28-35б. «3» - 19-27б.
Рефлексия.
Что у вас получилось? А что не получилось?
В чем были проблемы?
Кто чувствовал себя сегодня неуверенно?
А кто испытал чувство удовлетворения от проделанной работы?
Спасибо за урок.
РЕЙТИНГОВЫЙ ЛИСТ
По теме: «Квадратные уравнения»
Ф.И. , класс .
| № | Задания | Max баллов | Полученные баллы | Кто проверил | Кого проверил | Оценка |
| I | №1 №2 №3 №4 | . |
|
|
|
|
| II | №1 №2 |
|
|
|
|
|
| III |
| . |
|
|
|
|
| итог |
|
|
|
|
|
|
| Итого: |
А.Ж. Дюсекеева
учитель ГУ лицея, г. Аксу
Работа классного руководителя по воспитанию культуры здоровья
Система работы классного руководителя по воспитанию культуры здоровья школьников представляет собой сложную совокупность логически и организационно взаимосвязанных явлений, характеризующихся единством цели, задач, принципов, направлений, средств, форм, методов, приемов и отражающуюся в различных взаимодействиях классного руководителя с медицинской, психологической, социальной службами, семьями, учителем физкультуры, учителями предметниками, администрацией школы, основанных на программе культуры здоровья школьников.
Что же такое культура здоровья? Структура данного понятия такова:
Культура здоровья
Конативный элемент
Сформированная, активная, целенаправленная, самоконтролируемая деятельность, направленная на сохранение и укрепление здоровья
Когнитивный элемент
Приобретение,понимание,анализ,преобразованиеиспоьзование знаний о здоровье
Креативный элемент
Самосовершенствование, преодоление стереотипов, наличие личностных позитивных результатов образования в области культуры здоровья
При рассмотрении системы работы классного руководителя по воспитанию культуры здоровья школьников выделяют 4 этапа.
1-ый этап- реализация программы воспитания культуры здоровья в 1-4 классах, 2-ой этап – в 5-7 классах, 3-ий этап-в 8-9 классах, 4-ый этап- в 10-11 классах.
Целью реализация программы воспитания культуры здоровья в 5-7 классах является создание устойчивой положительной мотивационной сферы, направленной на формирование потребности каждого подростка вести здоровый образ жизни.
А для этого нужно:
- обеспечить условия для формирования положительной мотивации каждого школьника к овладению культурой здоровья;
- содействовать изучению школьниками составляющих здоровья и здорового образа жизни;
- помочь семьям подростков в формировании положительной мотивации воспитания здоровья личности каждого ребенка.
Ведь здоровье – это не просто отсутствие болезней, это состояние физического, психического и социального благополучия.
«От здоровья и жизнедеятельности детей зависит их духовная жизнь умственное развитие, прочность знаний, вера в свои силы».
Предметом острой тревоги стало отмечающееся в последнее время резкое ухудшение физического здоровья детей.
Здоровье детей школьного возраста, как и других групп населения, зависит от таких факторов, как состояние окружающей среды, здоровье родителей и наследственность, условия жизни и воспитания ребенка в семье, образовательном учреждении. Значимыми факторами, формирующими здоровье детей, является система воспитания и обучения, включая физическое воспитание.
Культура здорового и безопасного образа жизни, прежде всего - это осознанное, ежедневное выполнение учащимися здоровьесберегающих норм и правил. От уровня сформированности культуры здорового и безопасного образа жизни в детстве зависит последующий образ жизни человека, степень реализации его личностного потенциала. Состояние здоровья ребенка, его физическое развитие и даже внешний вид- это факторы, тесно связанные с поведением ребенка, его поступками, с формированием индивидуальных черт личности.
Какие могут быть этапы формирования культуры ЗОЖ:
1 этап- анализ состояния здоровья, организация режима дня, нагрузки детей, физкультурно-оздоровительная работа, рациональное питание, профилактика вредных привычек;
2 этап- лекции, беседы, по проблемам сохранения и укрепления здоровья;
проведение дней здоровья, конкурсов, праздников, направленных на пропаганду ЗОЖ;
3 этап-привлечение педагогов, мед. работников, психологов и родителей к совместной работе по проведению оздоровительных мероприятий и спортивных соревнований.
Состояние здоровья учащихся класса:
| ![]() Состояние здоровья Состояние здоровья
| Количество учащихся (oбщее 20) | Процентное соотношение |
| Практически здоровые | 8 | 40% |
| плоскостопие | 1 | 5% |
| спазм акомод. (зрение) | 5 | 25% |
| ВСД (сердечн) | 1 | 5% |
| Гипертон.синдром (внутрич.) | 2 | 10% |
| ДЖВП | 2 | 10% |
| Риск избыт. веса | 1 | 5% |
Занятость детей
| № | Ф.И. | Секции, кружки | учреждение |
| 1 | Белоусова Даша | акробатика | ДДТ |
| 2 | Воронкина Алина | музыка | Муз.школа |
| 3 | Глазунова Катя | акробатика | ДДТ |
| 4 | Завалко Миша | дзюдо | ДЮСШ |
| 5 | Мадирова Сандугаш | танц.кружок | ГДК |
| 6 | Корнейчук Данил | Баскетбол | Лицей |
| 7 | Умпелев Денис | дзюдо | ДЮСШ |
Каковы же существуют факторы здоровья:
-Личная гигиена
-Закаливание
-Двигательная активность
-Занятия физкультурой
-Отсутствие вредных привычек
-Рациональное питание
-Положительные эмоции
- Любовь к людям
Что же делается в нашем классе для достижения выше указанных целей и задач.
Учащиеся 5 «А» класса участвовали в таких школьных мероприятиях как:
1) День здоровья
2) Веселые старты между 5 «А» и 5 «Б» классами
3) Школьный турнир по баскетболу,пионерболу
Проводились классные часы:
Правильное питание – залог здоровья
Курение – коварная ловушка
Твое здоровье и личная гигиена
Проводились беседы:
Что такое ЗОЖ
ОРВИ и грипп
Полезные свойства горячего питания
Вирусный гепатит А
Профилактика бешенства
Жизнь без вредных привычек
Я провела внеклассное мероприятие по математике под названием : «Математика + физкультура».
Ежедневно проводятся физзарядки, дети участвуют во всех субботниках.
У каждого ребенка нет таких моментов, когда бы не было нужно заботиться о психологическом здоровье. Одним из таких этапов является подростковый период, который формально начинается с переходом ребенка из начальной школы в среднюю. Именно в этом возрасте дебютируют многие психические заболевания, увеличиваются количество школьных неврозов. Невроз здесь понимается как способ реагирования на те или иные сложности школьной жизни.
Поэтому, а также зная, что к факторам здоровья относятся: положительные эмоции, любовь к людям, то в связи с этим проводились неоднократные беседы, тренинги классные часы о дружбе, об общении друг с другом. А также классные собрания на темы:
« Все начинается с семьи», «Как научить ребенка слушать», Как научить детей общаться, дружить». Ведь нужно добиваться того, чтобы ребенку в доме жилось уютно, комфортно, спокойно, а это отражается на школьной жизни.
Обеспечив условия для формирования положительной мотивации каждого школьника к овладению культурой здоровья, помогая семьям подростков, мы хотим добиться снижения уровня заболеваемости детей, формирования ЗОЖ в семье.
И можно сказать, что укрепление здоровья учащихся будет способствовать более успешному решению основной задачи - качественному обучению детей.


 Получите свидетельство
Получите свидетельство Вход
Вход



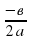
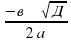
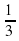 х2+
х2+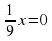 е)2х2-2х+0,5=0 к)
е)2х2-2х+0,5=0 к) 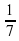 а=а2+4 (по 2б.)
а=а2+4 (по 2б.)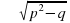 , если p2-q
, если p2-q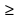 0
0 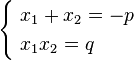 .
.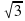 и х2 =2-
и х2 =2-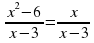 (2б.) б)
(2б.) б) 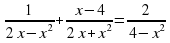 (4б.)
(4б.)









 Урок математики на тему: "Квадратные уравнения" (41.78 КB)
Урок математики на тему: "Квадратные уравнения" (41.78 КB)
 0
0 487
487 95
95 Нравится
0
Нравится
0



