Числовые неравенства, 8 класс

Название урока и класс:

Числовые неравенства, 8 класс

Цели:

Понятие числового отличия и универсального способа сравнения соотношений, научиться применять их к доказательству несоответствия.

Планируемые результаты:

Умение использовать данное определение для сравнения чисел и доказательства неравенств

Этап урока

Время (мин.)

Деятельность учителя

Организационный момент

2

Приветствие. Проверяет

готовность учащихся к уроку.

Эмоционально настраивает

класс на урок.

Приветствие. Проверяет

готовность учащихся к уроку.

Эмоционально настраивает

класс на урок.

Сегодня мы начинаем изучать важную и актуальную тему «Числовые неравенства». Если немного изменить слова великого китайского педагога Конфуция (жил более 2400 лет тому назад) можно сформулировать задачу нашего урока: «Я слышу и забываю. Я вижу и запоминаю. Я делаю и понимаю.» Давайте сформулируем вместе цель урока. (Учащиеся формулируют цель, учитель дополняет).

Актуализация знаний

6

Ребята, давайте вспомним всё, что мы знаем о неравенствах.

Ребята, посмотрите на доску, сравните:

Введение понятия

5

Что такое неравенство?

Неравенство - соотношение между числами (или любыми математическими выражениями, способными принимать численное значение), указывающее, какое из них больше или меньше другого.

Знаки неравенства ( › ; ‹)появились впервые в 1631г., но понятие неравенства, как и понятие равенства, возникло в глубокой древности. В развитие математической мысли без сравнения величин, без понятий «больше» и «меньше» нельзя было дойти до понятия равенства, тождества, уравнения.

-Какие правила использовали для сравнения чисел?

а) из двух положительных чисел больше то, модуль которого больше;

б) из двух отрицательных чисел больше то, модуль которого меньше;

в) любое отрицательное число меньше положительного;

г) любое положительное число больше нуля;

д) любое отрицательное число меньше нуля.

- Какое правило применяем для сравнения чисел, расположенных на координатной прямой?

(На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее.)

Заметим, что в зависимости от конкретного вида чисел мы использовали тот или иной способ сравнения. Это неудобно. Нам было бы легче иметь универсальный способ сравнения чисел, который охватил бы все случаи.

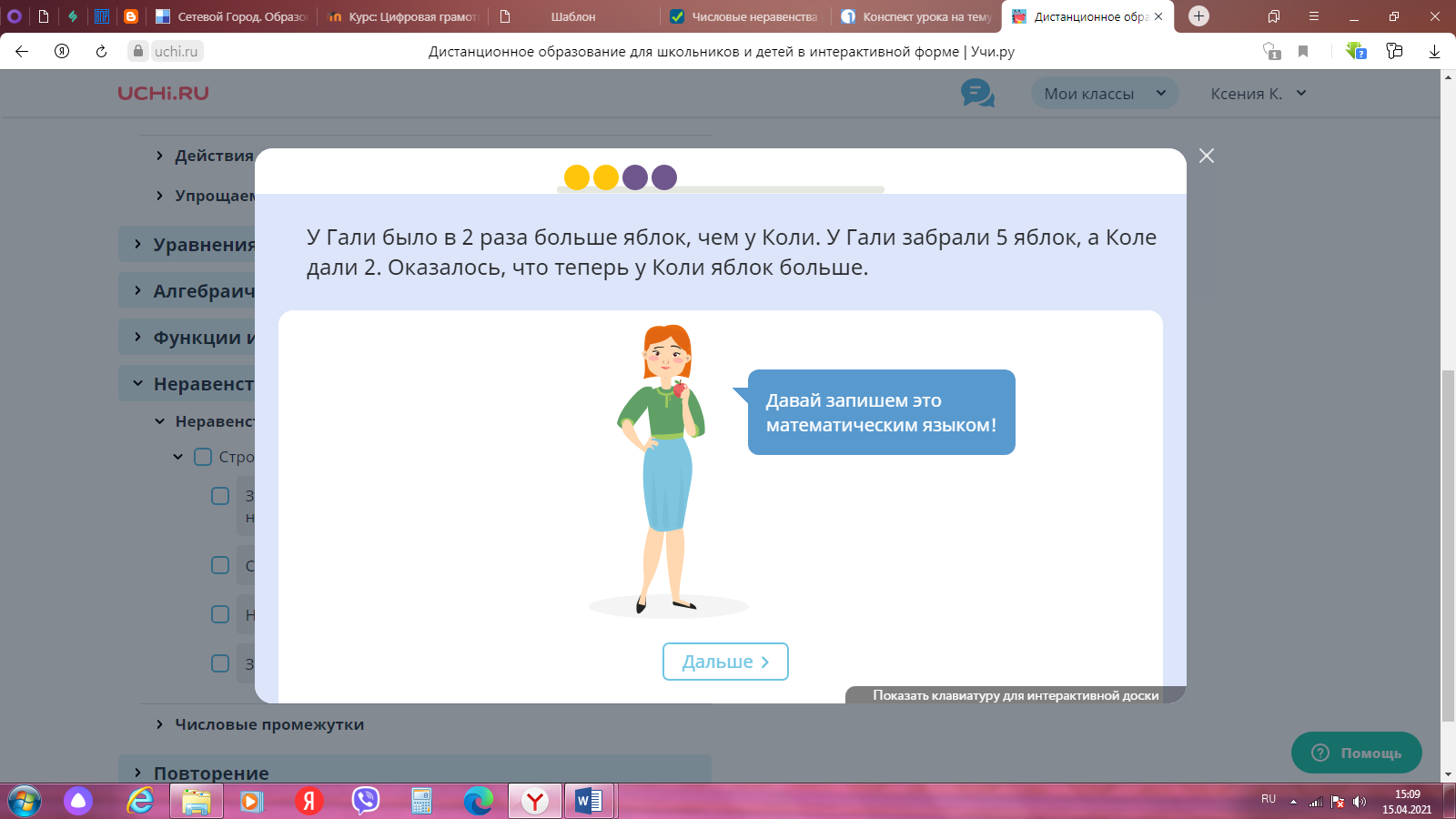
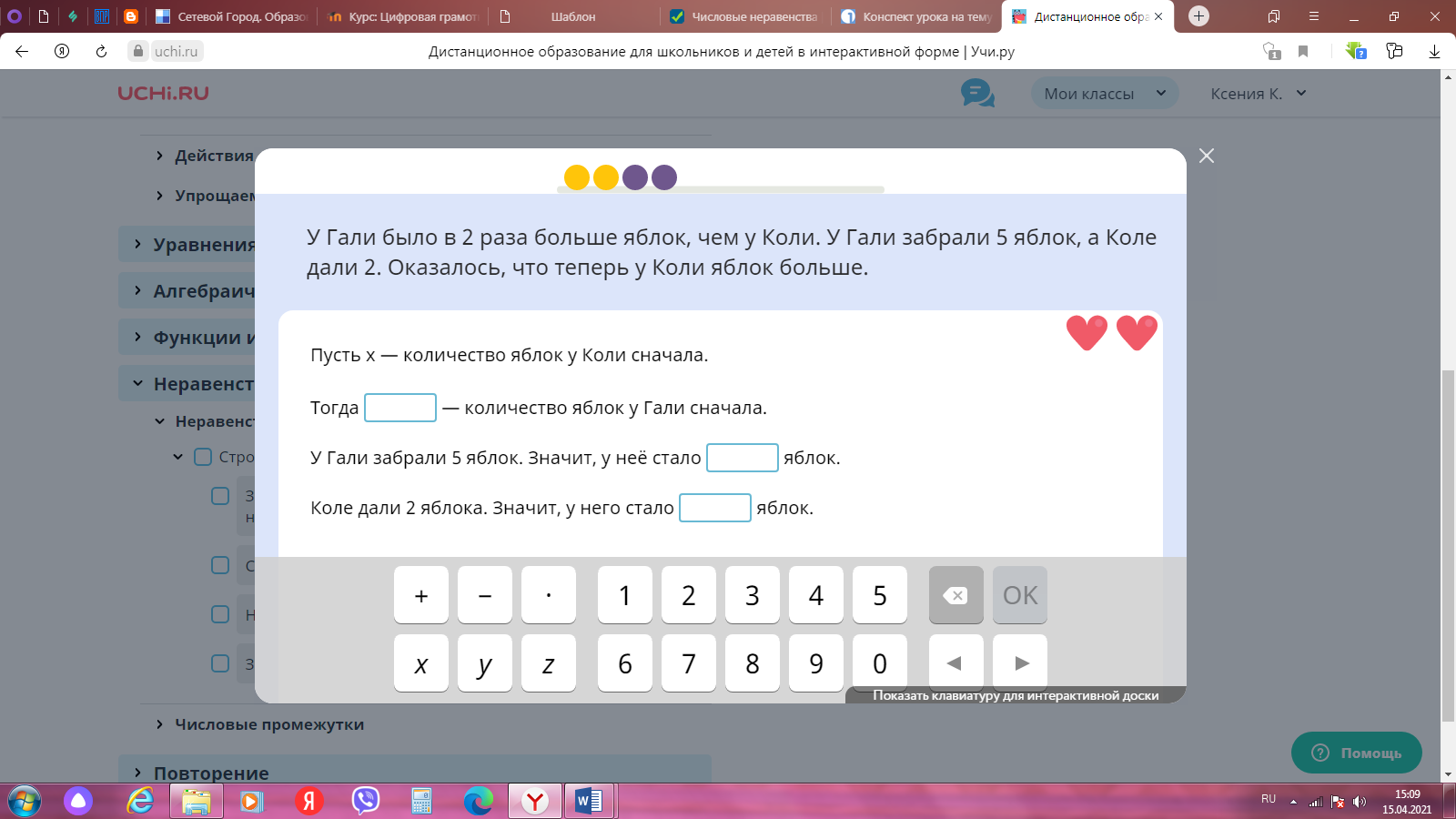
Работа по теме урока

7

Работа с заданиями от Учи.ру на интерактивной доске

Закрепление материала

5

Отлично, теперь читаем задание №729,731 и работаем вместе.

Запишите решение и ответы к заданию.

Физкультминутка

3

Закрепление материала

6

Замечательно. Теперь давайте возьмем в руки планшеты и каждый самостоятельно выполнит задания.

Подведение итогов

4

Что нового вы сегодня узнали на уроке? Что было непонятно?

Какое задание было самым сложным для вас?

Домашнее задание

2

Раздел «Задания из карточек» от учителя

40