Множества. Элементы множества.
Отношения между множествами.
Включение.
Равенство.
Числовые множества.
Множество всех подмножеств данного множества.
Операции над множествами.
5.1. Объединение множеств.
5.2. Пересечение множеств.
5.3. Разность множеств.
5.4. Симметрическая разность.
- Множества. Элементы множества
Одним из фундаментальных понятий математики является понятие множества. Оно обычно принимается за первоначальное и поэтому не определяется через другие.
Основатель теории множеств Георг Кантор описывал это понятие следующим образом: «Множество A есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое» (или «многое, мыслимое нами как единое целое».
Мы будем придерживаться следующего определения:
Множеством называют совокупность некоторых объектов, объединенных по какому-либо признаку.
Объекты, из которых состоит множество, называют его элементами. Множества обычно обозначаются большими буквами А, В, Х и т.д., а их элементы малыми а, b, c и т.д.
Если элемент а принадлежит множеству М, то пишут а ![]() М.
М.
Пустым называется множество, которое не содержит элементов, его обозначают символом .
Например, мы говорим о множестве решений уравнения до того, как узнаём, сколько оно имеет решений. Когда уравнение не имеет решений мы говорим, что множество решений уравнения х2+1=0 – пустое.
2. Отношения между множествами2.1. Включение
Если все элементы множества В принадлежат множеству А, то говорят, что множество В является подмножеством множества А. Записывается это следующим образом: В ⊏ А
Наглядно это отношение между множествами изображается ограниченными замкнутыми кривыми. Такое изображение называется диаграммой Венна (кругами Эйлера) 1.

| На рис. дана диаграмма Венна для случая, когда А⊏В |
|
Например, множество прямоугольников включается в множество параллелограммов (всякий прямоугольник – параллелограмм).
Из определения подмножества следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение А А. Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А. В А
Полагают также, что пустое множество является подмножеством любого множества.
Это вполне естественно, т.к. пустое множество не содержит ни одного элемента и, следовательно, в нём нет элемента, который не принадлежал бы любому другому множеству.
2.2. Равенство
Два множества называются равными, если каждый элемент множества А является одновременно элементом множества В и каждый элемент множества В является элементом множества А. Записывается это следующим образом: А=В
Например, А = {1, 2}; В = {2,1} А = В
В математике чаще всего приходится иметь дело со множествами, элементами которых являются числа. Такие множества называются числовыми. Различают конечные и бесконечные множества. Например, множество всех двузначных чисел - конечное, а множество отрицательных чисел - бесконечное.
Для числовых множеств удобно ввести специальные обозначения. Мы будем пользоваться следующими:
| Множество всех натуральных чисел | N |
| Множество всех целых чисел | Z |
| Множество всех рациональных чисел | Q |
| Множество всех вещественных (действительных) чисел | R |
Натуральные числа – это числа, возникающие в результате счёта предметов. N = {1, 2, 3, …..}.
Целые числа – это натуральные числа, им противоположные и ноль. Z = {…-3, -2, -1, 0, 1, 2, 3, …}. Таким образом N Z.
Рациональные числа – это числа вида a/b. Всякое рациональное число может быть представлено либо в виде конечной, либо в виде бесконечной десятичной дроби. Любое целое число является рациональным, т.к. его можно представить в виде a/1 = a. Таким образом N Z Q.Множество действительных чисел является расширением множества рациональных чисел. Оно включает в себя числа, которые нельзя представить в виде конечной или периодической дроби, например, √2. Их называют иррациональными. Таким образом N Z Q R.
4. Множество всех подмножеств данного множества
Множество всех подмножеств некоторого множества М обозначается символом Р(М). Р – первая буква латинского слова parties (части).
Например, если М = {a, b, c}, то
Р(М) = {, {а}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.
Рассмотрим задачу определения числа всевозможных подмножеств конечного множества. Пусть М – множество, состоящее из n элементов. Будем говорить «n-элементное» множество. Определим, сколько всего подмножеств можно образовать из элементов множества М. Задачу решим методом математической индукции, который основан на следующем принципе:
Выражение А(n) считается истинным для всех натуральных значений переменной, если выполнены условия:
Выражение А(n) истинно для n=1
Из предположения, что А(n) истинно для n=k, (где k произвольное натуральное число) следует, что А(n) истинно и для следующего значения n=k+1
Пусть М – пустое множество, тогда Р(М) = {}, т.е. Р(М) = 1
Пусть М = {a}, тогда Р(М) = {, {a}}, т.е. Р(М) = 2
Пусть М = {a, b}, тогда Р(М) = {, {a}, {b}, {a,b}}, т.е. Р(М) = 4
Пусть М = {a,b,c}, тогда Р(М) = {, {a}, {b}, {a,b}, {c}, {a,c}, {b,c}, {a,b,c}}, т.е. Р(М) = 8
Из этих частных случаев можно заключить, что число всевозможных частей «n-элементного» множества равно 2n.
Если множество состоит из n элементов, то число всех его подмножеств равно 2n.
5.1. Объединение множеств
Объединением множеств А и В называется множество, элементы которого принадлежат либо множеству А, либо множеству В. Объединение множеств А и В обозначается А U В.
Э то определение можно записать кратко так:
то определение можно записать кратко так:
А U В = {x|x![]() A или x
A или x![]() B}
B}
| На диаграмме заштриховано объединение. |
|
Пусть А = {a,b,c,d}, B = {x,y,z}
Согласно определения А U В = {a,b,c,d,x,y,z}
При решении неравенств часто приходится образовывать объединение множеств. Пусть, например, требуется решить неравенство |х-2| 1 на множестве R (x![]() R).
R).

|
|х-2| 1 равносильно | x-2 |
| x |
| |
|
|
|
|
| ||
| x-2 1 |
| x 3 |
| ||
| На числовой прямой это можно изобразить так:
| | ||||
А U В = (-∞, 1) U (3, +∞).
5.2. Пересечение множеств
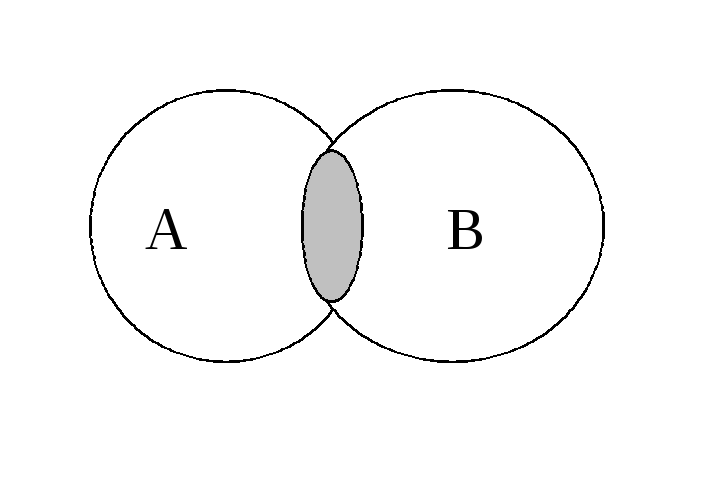
Пересечением двух множеств А и B называется такое множество, элементы которого принадлежат и множеству А и множеству В, т.е. их общая часть. Пересечение множеств обозначаются: А ∩В
Это определение можно записать кратко так:
А∩В = {x|x![]() A и x
A и x![]() B}
B}
| На диаграмме заштриховано пересечение. | |
Рассмотрим два множества: Х={a, b, c, d}, Y={a, b, f, k}
Элементы а и b принадлежит обоим множествам, т.о. множество {a,b} является пересечением рассмотренных множеств Х и Y:
X∩Y = {a, b, c, d}∩{a, b, f, k}= {a, b}
При решении неравенств часто приходится образовывать пересечение множеств. Пусть, например, требуется решить неравенство |х-2| R (x![]() R).
R).

|
|х-2| | x-2 -1 |
| x 1 |
| |
|
|
|
|
| ||
| x-2 1 |
| x 3 |
| ||
|
|
|
|
|
| |
| На числовой прямой это можно изобразить так:
| | ||||
А∩В = (-∞, 3) ∩(1, +∞) = (1, 3)
| Если множества А и В не имеют общих элементов, то их пересечением является пустое множество А∩В= |
|
Например, пересечением множества четных чисел со множеством нечетных чисел – пустое. Пересечение любого множества с пустым множеством есть пустое множество. А∩![]() =
=![]() .
.
- Разность множеств
Разностью множеств А и В называют множество всех тех элементов множества А, которые не входят в множество В. Разность обозначается: А\В.
Например, А={1,2,3}, B={1,2} A\B={3}
Это определение можно записать кратко так: А\В = {x|x![]() A и x
A и x![]() B}
B}
Симметрическая разность
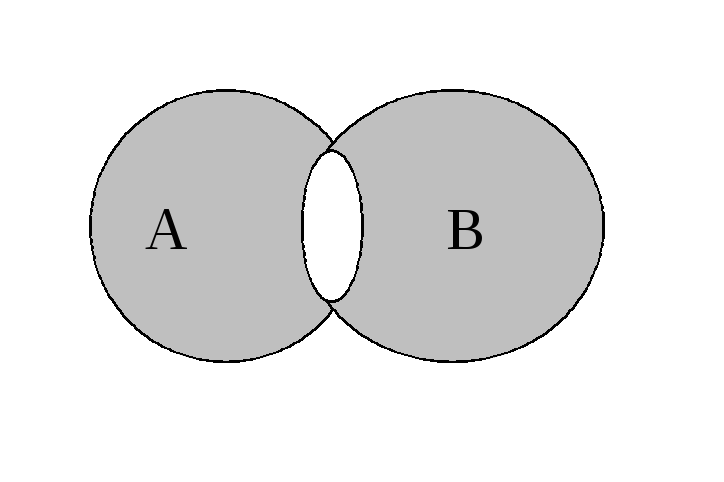
Симметрической разностью множеств А и В называют множество, представляющее собой объединение множеств A\B и B\A. Симметрическая разность обозначается: АΔВ =(А\В) U (В\А).
| На диаграмме симметрическую разность представляют так: | |
Например, А={1,3,5,7,9,11,13}, B={1,2,3,4,5,6,7}
AΔB={2,4,6,9,11,12,13}
Задача 1. Из 40 студентов курса 32 изучают английский язык, 21 - немецкий язык, а 15 - английский и немецкий языки. Сколько студентов курса не изучает ни английский, ни немецкий языки?
Решение. Пусть А - множество студентов курса, изучающих английский язык, В - множество студентов курса, изучающих немецкий язык, С - множество всех студентов курса. По условию задачи: п(А) = = 32, п(В) = 21, п(А∩В) = 15, п(С) = 40. Требуется найти число студентов курса, не изучающих ни английского, ни немецкого языка.
1 способ.
1) Найдем число элементов в объединении данных множеств А и В.
Для этого воспользуемся формулой (2):
п(А U В) = п(А) + п(В) - п(А ∩ В) = 32 + 21 - 15 = 38.
2) Найдем число студентов курса, которые не изучают ни английский, ни немецкий языки: 40 - 38 = 2.
2 способ.
1) Изобразим данные множества при помощи кругов Эйлера и определим число элементов в каждом из непересекающихся подмножеств.
Так как в пересечении множеств А и В содержится 15 элементов, то студентов, изучающих только английский язык, будет 17 (32 - 15 = 17), а студентов, изучающих только немецкий, - 6 (21 - 15 = 6).
Тогда п(А U B) = 17 + 15 + 6 = 38, и, следовательно, число студентов курса, которые не изучают ни английский, ни немецкий языки, будет 40 - 38 = 2.
1 По имени английского учёного Джона Венна (1834-1923). Намного раньше Венна Леонард Эйлер использовал круги для изображения отношения между множествами.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Теория множеств (180 KB)
Теория множеств (180 KB)
 0
0 994
994 6
6 Нравится
0
Нравится
0


