МКОУ СОШ №6 г.о. Баксан
Кабардино – Балкарской Республики
Программа элективного курса
по математике в 9 классе
«Множества»
Автор: учитель математики
Балкизова Инга Беталовна
Пояснительная записка
Некоторые школьники обладают хорошим математическим аппетитом.
Их не удовлетворяют порции математики, отмеренные школьной программой.
Понятие множества является одним из основных понятий математики.
Свойства конечных множеств были учащемуся известны из жизненного опыта - складывать и вычитать конечные множества приходится уже малым детям. Новыми являются для учащихся точные математические формулировки соответствующих понятий. А свойства бесконечных множеств уже совсем необычны. Теория множеств является одной из основ, на которых базируются почти все математические дисциплины - топология, функциональный анализ, общая алгебра и т.д.
Цели курса:
-помочь, повысить уровень понимания и практической подготовки в таких вопросах как: 1) множества из окружающего мира, 2) применение множеств к теории уравнений и неравенств 3) истолкование на языке теорий множеств таких понятий, как система уравнений и неравенств, совокупность уравнений и неравенств;
-способствовать интеллектуальному развитию учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе;
-помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы;
Задачи курса:
-научить учащихся решать уравнения, неравенства, систем уравнений и неравенств, совокупности уравнений и неравенств с точки зрения теоретико-множественных позиций;
- помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы.
Содержание программы.
Тема 1. (2 ч.) Понятия множества. Способы задания множеств. Пустое множество.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений. Формы контроля: проверка самостоятельно решенных задач.
Тема2. (2 ч.) Числовые множества. Множество корней уравнения. Область определения уравнения.
Методы обучения: объяснения, выполнение тренировочных упражнений. Формы контроля: проверка самостоятельно решенных задач.
Тема 3. (4 ч.) Множество точек на плоскости. Уравнения линий. Решение неравенств с двумя неизвестными.
Методы обучения: объяснение, выполнение тренировочных упражнений. Формы контроля: проверка самостоятельно решенных задач.
Тема 4 (6 ч.) Подмножества. Пересечение множеств. Системы уравнений и неравенств.
Методы обучения: лекция, выполнение тренировочных упражнений. Форма контроля: проверка самостоятельно решенных задач.
Тема 5 (4 ч.) Объединение множеств. Совокупность уравнений и неравенств.
Методы обучения: лекций, объяснение, выполнение тренировочных упражнений Форма контроля: проверка самостоятельно решенных задач.
Тема 6 (3 ч.) Разбиение множеств. Вычисление множеств. Алгебра множеств.
Методы обучения: объяснение, выполнение тренировочных упражнений. Форма контроля: проверка самостоятельно решенных задач.
Тема 7 (2 ч.) Счетные множества
Метод обучения: объяснение, выполнение тренировочных упражнений. Форма контроля: проверка самостоятельно решенных задач.
Тема 8 (3 ч.) Взаимно-однозначное соответствие. Мощность множества.
Метод обучения: объяснение, выполнение тренировочных упражнений Форма контроля: проверка самостоятельно решенных задач.
Контрольная работа (I ч.)
Учебно – тематический план
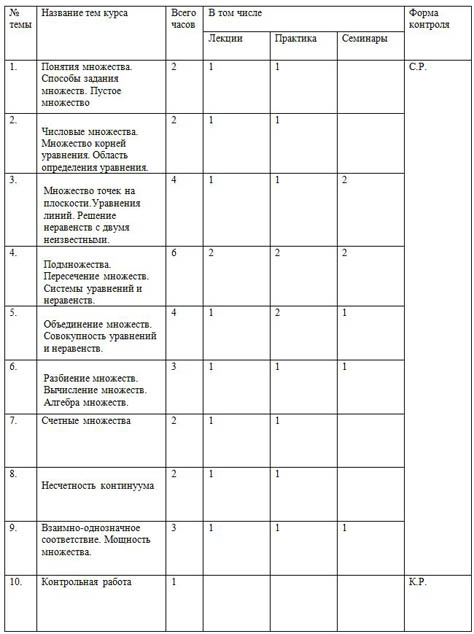
| № темы | Название тем курса | Всего часов | В том числе | Форма контроля |
| Лекции | Практика | Семинары |
| 1. | Понятия множества. Способы задания множеств. Пустое множество | 2 | 1 | 1 |
| С.Р. |
| 2. | Числовые множества. Множество корней уравнения. Область определения уравнения. | 2 | 1 | 1 |
|
| 3. | Множество точек на плоскости.Уравнения линий. Решение неравенств с двумя неизвестными. | 4 | 1 | 1 | 2 |
| 4. | Подмножества. Пересечение множеств. Системы уравнений и неравенств. | 6 | 2 | 2 | 2 |
| 5. | Объединение множеств. Совокупность уравнений и неравенств. | 4 | 1 | 2 | 1 |
| 6. | Разбиение множеств. Вычисление множеств. Алгебра множеств. | 3 | 1 | 1 | 1 |
| 7. | Счетные множества
| 2 | 1 | 1 |
|
| 8. | Несчетность континуума | 2 | 1 | 1 |
|
| 9. | Взаимно-однозначное соответствие. Мощность множества. | 3 | 1 | 1 | 1 |
| 10. | Контрольная работа | 1 |
|
|
| К.Р. |
Литература по методике преподавания курса
Серпинский В.О. О теории множеств.
Кордемелий Б.А. Увлечь школьников математикой
Курант Р. Роббинс Г. Что такое математика?
Нивен А. Числа рациональные и иррациональные
Петер Р. Игра с бесконечностью
Радемахер Г. Теплиц О. Числа и фигуры
Беккенбах Э. «Введение в неравенства».
Кураш А.Г. Алгебраические уравнения произвольных степеней.
Литература для учащихся.
Сикорский К.П. «Решение задач по общему курсу»
Н.Я.Виленкин. Элементы теории множеств.
Блох А.Я. Числовые множества.
Потапов М.К., Олежник С.Н., Нестеренко Ю.В. Математика.
Примеры решения задач, теория.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Программа элективного курса по математике "Множества" (79 КB)
Программа элективного курса по математике "Множества" (79 КB)
 0
0 460
460 5
5 Нравится
0
Нравится
0



