МБОУ «Новошешминская средняя общеобразовательная школа
Новошешминского муниципального района РТ»
Элективный курс
«В мире комплексных чисел»
Авторы:
Иванова Юлия Николаевна, учитель математики и информатики МБОУ «Новошешминская СОШ»,
Данилова Светлана Николаевна, учитель математики МБОУ «Новошешминская СОШ»,
Лазарева Ольга Ивановна, учитель математики МБОУ «Новошешминская СОШ».
Пояснительная записка
Программа элективного курса «В мире комплексных чисел» предусматривает углубленное изучение теории чисел и предназначена для учащихся 10-11 классов общеобразовательной школы.
Предлагаемый курс является развитием системы ранее приобретенных программных знаний. Процесс расширения понятия числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами самой математики. Сначала для счета предметов использовались натуральные числа. Затем необходимость выполнения деления привела к понятию дробных положительных чисел; далее необходимость выполнения вычитания – к понятиям нуля и отрицательных чисел; наконец необходимость извлечения корней из положительных чисел – к понятию иррациональных чисел. Все перечисленные операции выполнимы на множестве действительных чисел. Однако остались невыполненными на этом множестве операции извлечение квадратного корня из отрицательного числа. Значит имеется потребность в дальнейшем расширении понятия числа, в появлении новых чисел в отличие от действительных. Такие числа были названы комплексными, имеющие вид а+bi, где а и b есть действительные числа. Отказываться изучать выражения данного вида лишь потому, что символ i не есть действительное число, означало бы допустить очень большое торможение в развитии алгебры, развитии её методов, многие алгебраические действия остались бы невыполненными. Например, нельзя было бы выполнить действие извлечения корня 6-й степени из отрицательного числа. Учение о числах вида а+bi и теории, развитые на основе этого учения, оказались мощным средством, позволившим успешно решить крупнейшие теоретические и практические проблемы. Например, знаменитый русский ученый Николай Егорович Жуковский блестяще использовал эти теории для расчета крыльев самолета. Эти теории с огромным успехом применяются в электротехнике, гидромеханике, аэромеханики, теории упругости и во многих других отделах естествознания и техники. Необходимость изучения данного курса также состоит том, что при решении упражнений на повторение в 11 классе по учебнику Ш.А.Алимова предлагается выполнить задания с комплексными числами, но теоретический материал в 10 – 11 классах по этой теме не рассматривается. Все свойства, входящие в элективный курс, и их доказательства не вызовут трудности у учащихся, т.к. не содержат громоздких выкладок.
На изучение тем отводится 17 часов, из них 16 часов - на практическое решение задач, 1 час – на определение успешности усвоения материала в форме тестирования или зачета.
При изучении теории комплексных чисел применяются опорные конспекты, предусмотрено использование интерактивной доски и индивидуальная работа учащихся по усвоению теории.
Цели курса:
- расширить кругозор учащихся непосредственных связей школьной программы математики с наукой и ее приложениями;
- сформировать представление о теории комплексных чисел.
Задачи курса:
- познакомить учащихся с понятием комплексного числа; научить выполнять основные арифметические операции на множестве комплексных чисел;
- сформировать умение решать упражнения по данной теме;
- показать необходимость знаний данного курса в развитии математики и во многих отделах техники и естествознания;
- развивать интеллектуальные способности, логическое мышление;
- овладение конкретными математическими знаниями, необходимыми для применения на практике, изучения смежных дисциплин ( физики), продолжения образования и сознательного выбора профессии;
- показать прикладную значимость математики.
В результате изучения курса учащиеся должны:
- понимать содержательный смысл теории комплексных чисел, как действенного инструмента при использовании математических методов в различных областях науки;
- при вычислении сочетать устные и письменные приемы, использовать приемы, рационализирующие вычисления.
Структура программы комплексных чисел является обучающей и содержит:
Пояснительную записку.
Цели курса.
Содержание курса.
Примерное тематическое планирование.
Требования к умениям и навыкам.
Методические рекомендации.
Литература
Учебно-тематический план
| №
п/п | Тема | Количество часов | Формы проведения | Образовательный продукт |
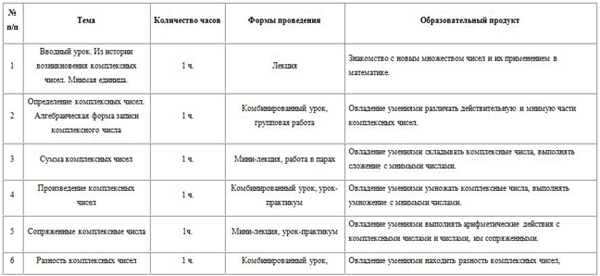
| 1 | Вводный урок. Из истории возникновения комплексных чисел. Мнимая единица. | 1 ч. | Лекция | Знакомство с новым множеством чисел и их применением в математике. |
| 2 | Определение комплексных чисел. Алгебраическая форма записи комплексного числа | 1 ч. | Комбинированный урок, групповая работа | Овладение умениями различать действительную и мнимую части комплексных чисел. |
| 3 | Сумма комплексных чисел | 1 ч. | Мини-лекция, работа в парах | Овладение умениями складывать комплексные числа, выполнять сложение с мнимыми числами. |
| 4 | Произведение комплексных чисел | 1 ч. | Комбинированный урок, урок-практикум | Овладение умениями умножать комплексные числа, выполнять умножение с мнимыми числами. |
| 5 | Сопряженные комплексные числа | 1ч. | Мини-лекция, урок-практикум | Овладение умениями выполнять арифметические действия с комплексными числами и числами, им сопряженными. |
| 6 | Разность комплексных чисел | 1 ч. | Комбинированный урок,
урок-практикум | Овладение умениями находить разность комплексных чисел, находить разность с мнимыми числами. |
| 7 | Частное комплексных чисел | 1 ч. | Мини-лекция, групповая работа | Овладение умениями выполнять деление комплексных чисел. |
| 8 | Модуль и аргумент комплексного числа | 1 ч. | Мини-лекция, лабораторная работа | Овладение умениями находить модуль комплексного числа. |
| 9 | Геометрическая интерпретация комплексного числа | 1 ч. | Мини-лекция, работа в парах | Овладение умениями строить сумму и разность комплексных чисел, противоположные комплексные числа. |
| 10 | Комплексная плоскость. Решение задач | 1 ч. | Урок-практикум | Овладение умениями находить множество точек комплексной плоскости. |
| 11 | Тригонометрическая форма комплексного числа | 1 ч. | Мини-лекция, работа в парах | Овладение умениями записывать комплексные числа в тригонометрической форме. |
| 12 | Нахождение аргументов комплексных чисел | 1 ч. | Урок-практикум | Овладение умениями находить аргументы комплексных чисел. |
| 13 | Свойства модуля и аргумента комплексного числа | 1 ч. | Мини-лекция, групповая работа | Овладение умениями выполнения умножения и деления комплексных чисел в тригонометрической форме. |
| 14 | Умножение и деление комплексных чисел в тригонометрической форме записи | 1 ч. | Урок-практикум | Закрепление умений выполнения умножения и деления комплексных чисел в тригонометрической форме, используя изученные свойства. |
| 15 | Квадратное уравнение с комплексным неизвестным | 1 ч. | Мини-лекция, урок-практикум | Овладение умениями находить корни квадратных уравнений при отрицательном дискриминанте. |
| 16 | Примеры решения алгебраических уравнений | 1 ч. | Урок-практикум | Закрепление умений нахождения корней алгебраических уравнений, используя комплексные числа. |
| 17 | Урок обобщения и систематизации знаний | 1 ч. | Тестирование | Умение работать с комплексными числами. |
Тема 1 Вводный урок. Из истории возникновения комплексных чисел. Мнимая единица.
Содержание темы:
Знать значение математического образования;
Основные цели математического образования;
Общие принципы школьного математического образования;
Нормативная база школьного математического образования;
Иметь ясное представление о множествах чисел;
Уметь выполнять операции над числами.
Исторический материал.
Мнимая единица.
Тема 2 Определение комплексных чисел. Алгебраическая форма записи комплексного числа
Содержание темы:
Определение комплексных чисел.
Мнимая единица.
Мнимые числа.
Алгебраическая форма комплексного числа.
Действительная часть комплексного числа.
Мнимая часть комплексного числа.
Тема 3 Сумма комплексных чисел
Содержание темы:
Тема 4 Произведение комплексных чисел
Содержание темы:
Тема 5 Сопряженные комплексные числа
Содержание темы:
Определение сопряжённых чисел.
Теоремы о сопряжённых комплексных числах. (4)
Следствия из теорем о сопряжённых числах.
Тема 6 Разность комплексных чисел
Содержание темы:
Тема 7 Частное комплексных чисел
Содержание темы:
Тема 8 Модуль и аргумент комплексного числа
Содержание темы:
Понятие модуля комплексного числа и аргумента комплексного числа.
Радиан, как единица измерения углов.
Главное значение аргумента.
Обозначение аргумента.
Тема 9 Геометрическая интерпретация комплексного числа
Содержание темы:
Тема 10 Тригонометрическая форма комплексного числа
Содержание темы:
Тема 11 Свойства модуля и аргумента комплексного числа
Содержание темы:
Тема 12 Умножение и деление комплексных чисел в тригонометрической форме записи
Содержание темы:
Тема 13 Квадратное уравнение с комплексным неизвестным
Содержание темы:
Общий вид квадратных уравнений.
Формула дискриминанта квадратного уравнения.
Формула корней квадратного уравнения.
Общий вид квадратных уравнений с комплексными коэффициентами.
Алгоритм решения квадратных уравнений с комплексными коэффициентами.
Требования к математической подготовке.
учащиеся должны знать и правильно употреблять термины «комплексное число», «мнимая единица»;
знать методы решения уравнений;
знать основные теоремы и формулы;
уметь решать алгебраические уравнения;
проводить полные обоснования при решении задач.
Контроль и оценка ЗУН.
Устный опрос по конспекту
Парный и групповой взаимоконтроль.
Самоконтроль.
Тестирование.
Творческие работы учащихся.
Возможные критерии оценок:
«хорошо/отлично» - учащийся освоил теоретический материал курса, получил навыки в его применении при решении конкретных задач; продемонстрировал умение работать самостоятельно.
«зачет» - учащийся освоил наиболее простые идеи и методы курса, успешно выполнял простые задания.
Литература для учащихся
Ю. М. Колягин, Ю. В. Сидоров и др. Алгебра и начала анализа: Учебник для 11 класса общеобразовательных учреждений. – М.: Мнемозина, 2001.
С. М. Никольский, М. К. Потапов и др. Алгебра и начала анализа: Учебник для 11 класса общеобразовательных учреждений. – М.: Просвещение, 2007.
Научно- практический журнал «Математика для школьников» №1 2006г.
Литература
М. Я. Выгодский, Справочник по элементарной математике . – М.: Наука ,1986.
Н. Ш. Кремер, Высшая математика для экономистов. – М.: Юнити, 2001.
Учебно- методическая газета «Математика», №2 2007, №16 2006.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Программа элективного курса "В мире комплексных чисел" (92 КB)
Программа элективного курса "В мире комплексных чисел" (92 КB)
 0
0 979
979 69
69 Нравится
0
Нравится
0







