Круги Эйлера
Цель: показать, что применение кругов Эйлера придает задачам наглядность и простоту; круги Эйлера с успехом применяются в логических задачах для изображения множеств истинности высказываний.
1. Введение
Л еонард Эйлер (1707 - 1783).
еонард Эйлер (1707 - 1783).
Эйлеру повезло: он родился в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и ученые, не желавшие тратить дорогое рабочее время на гражданские смуты или религиозные распри. Так переселилась в Базель из Голландии семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию и вскоре сделался достойным членом базельского питомника гениев.
Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику под руководством, первыми образцами которых явились классические монографии Эйлера. Он был, прежде всего, математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный.
Его называли идеальным математиком 18 века.
Л еонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Джон Венн — британский логик и философ; основные труды в области логики классов; и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логика, статистика, компьютерные науки.
еонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Джон Венн — британский логик и философ; основные труды в области логики классов; и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логика, статистика, компьютерные науки.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера-Венна».
Этот метод даёт более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
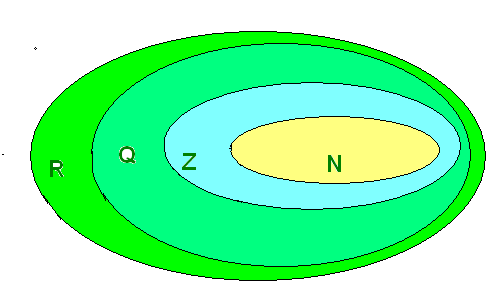
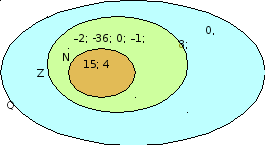
В нашем учебнике по математике множество всех действительных чисел Эйлер изображено с помощью этих кругов: N - Множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вех действительных чисел.
2. Решение задач с помощью кругов Эйлера
Задача 1. В гостях на уроке математики присутствовало 3 математика, директор и завуч. Из них преподаёт только математику один человек. Возможно ли это, если да, то показать это с помощью кругов Эйлера-Венна.
З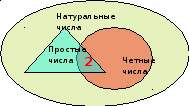 адача 2. Интересная задача родилась при изучении простых чисел. Даны множества: натуральны, четные и простые числа. Найти пересечение этих множеств.
адача 2. Интересная задача родилась при изучении простых чисел. Даны множества: натуральны, четные и простые числа. Найти пересечение этих множеств.
Ответ: 2.
Задача 3. Все мои друзья занимаются каким-нибудь видом спорта. 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?
Решение: Обратимся к кругам Эйлера:
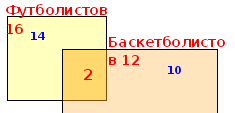
Изобразим два множества (можно вводить обозначения их не только кругами), так как два вида спорта. В одном я буду фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом. Поскольку некоторые из моих друзей увлекаются и тем и другим видом спорта, то квадраты нарисую так, чтобы у них была общая часть (пересечение). В этой общей части ставим цифру 2. В оставшейся части «футболистов» круга ставим цифру 14 (16 − 2= 14). В свободной части «баскетболистов» круга ставим цифру10 (12 − 2 = 10). А теперь рисунок сам подсказывает, что всего у меня 14 + 2 + 10 = 26 друзей.
Ответ: 26 друзей.
Задача 4.
Дано множество: А = {–16; 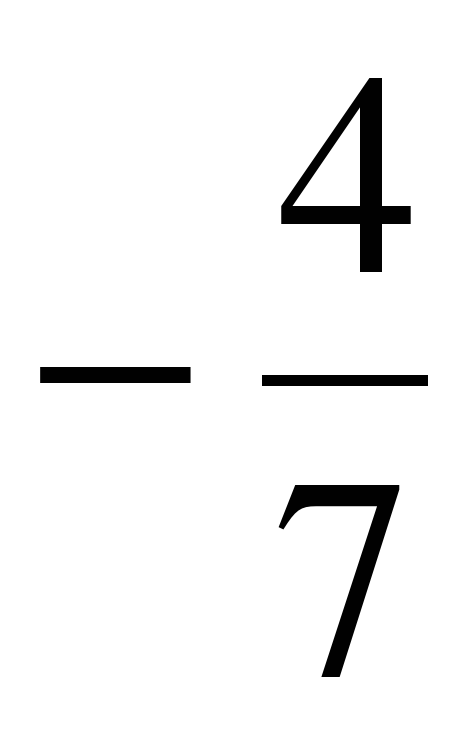 ; –0,3; 9; 1
; –0,3; 9; 1 ; 0; –5; 2; 4,8}. Составьте из элементов этого множества подмножества: 1) В – отрицательных рациональных чисел; 2) С – натуральных чисел; 3) D – целых чисел; 4) Е – целых отрицательных чисел. Постройте круги Эйлера-Венна множеств A, B, C, D и E.
; 0; –5; 2; 4,8}. Составьте из элементов этого множества подмножества: 1) В – отрицательных рациональных чисел; 2) С – натуральных чисел; 3) D – целых чисел; 4) Е – целых отрицательных чисел. Постройте круги Эйлера-Венна множеств A, B, C, D и E.
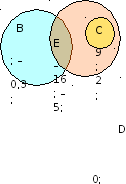
Задача 5.
В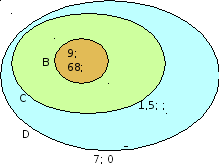 ыберите из множества А = {1,5; –7;
ыберите из множества А = {1,5; –7; 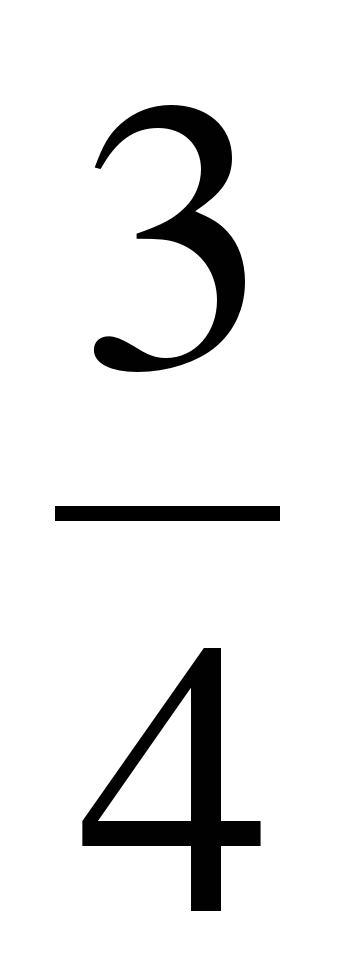 ; 0; 9; –2
; 0; 9; –2 ; 68} подмножество: 1) В – натуральных чисел; 2) С – целых чисел; 3) D – рациональных чисел. Постройте круги Эйлера-Венна множеств. А, В, С и D и отметьте на ней элементы множества А.
; 68} подмножество: 1) В – натуральных чисел; 2) С – целых чисел; 3) D – рациональных чисел. Постройте круги Эйлера-Венна множеств. А, В, С и D и отметьте на ней элементы множества А.
Задача 6
Дано множество: А = {–2; 0,8; 15; 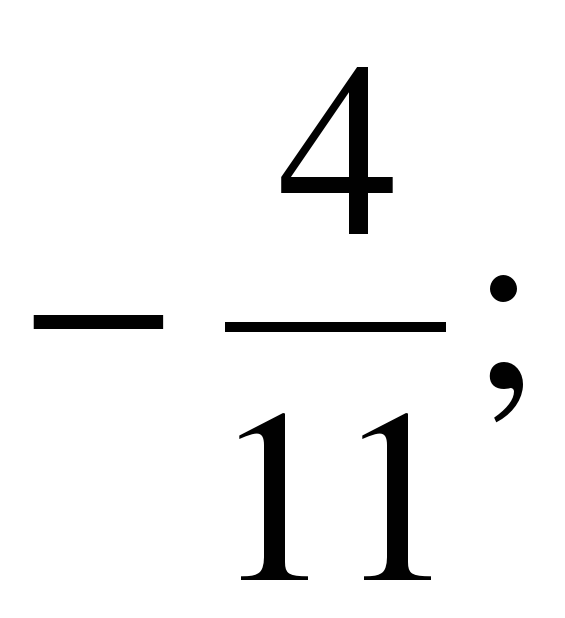 –36; 0;
–36; 0; 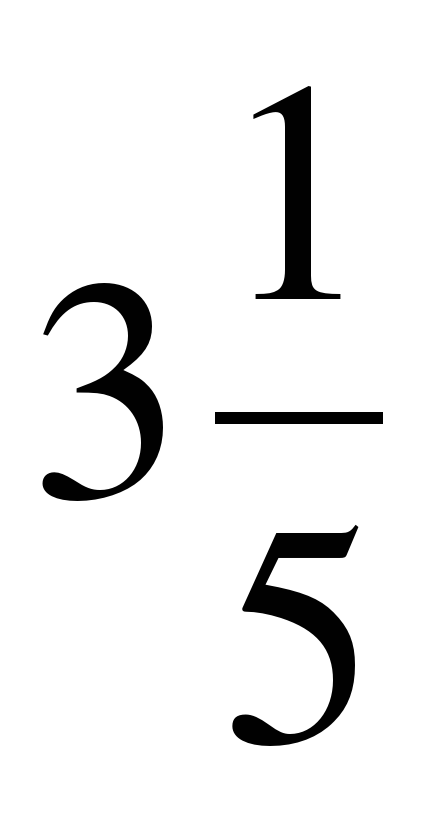 ; 4}. Нарисуйте круги Эйлера-Венна множеств N, Z, Q и отметьте на ней элементы множества А.
; 4}. Нарисуйте круги Эйлера-Венна множеств N, Z, Q и отметьте на ней элементы множества А.
Задача 7.
Выберите из множества А = {5; 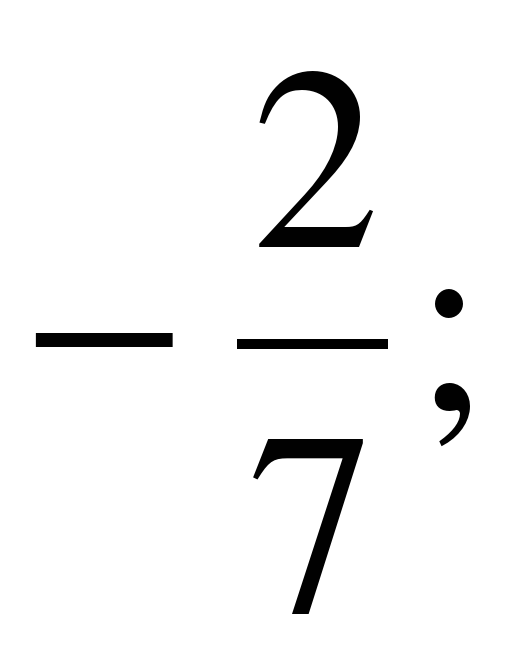 0; –12; –7,8;
0; –12; –7,8; 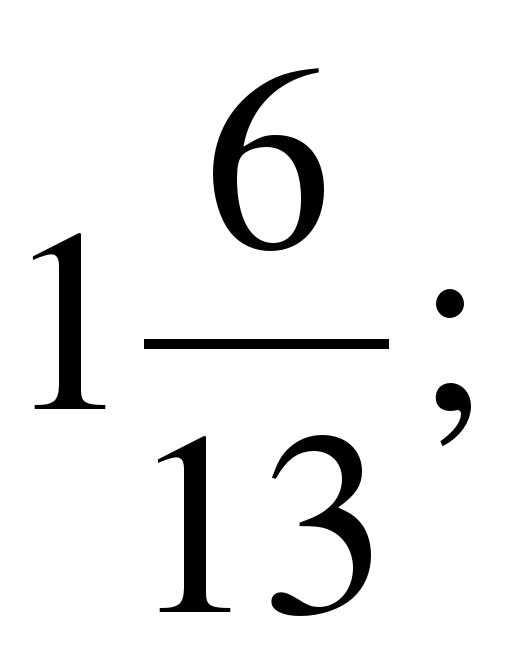 –0,95; 8,6; 21;
–0,95; 8,6; 21; 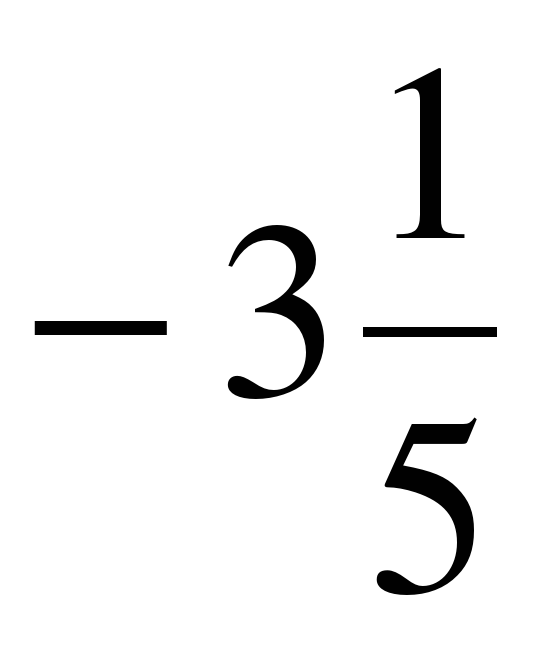 } подмножество: 1) В – положительных чисел; 2) С – отрицательных чисел; 3) D – целых чисел; 4) Е – натуральных чисел; 5) F – неотрицательных целых чисел; 6) К – отрицательных дробных чисел. Постройте круги Эйлера-Венна множеств A, B, C и D. Обведите на ней красным карандашом множество Е, зеленым – множество F, а желтым – множество К.
} подмножество: 1) В – положительных чисел; 2) С – отрицательных чисел; 3) D – целых чисел; 4) Е – натуральных чисел; 5) F – неотрицательных целых чисел; 6) К – отрицательных дробных чисел. Постройте круги Эйлера-Венна множеств A, B, C и D. Обведите на ней красным карандашом множество Е, зеленым – множество F, а желтым – множество К.
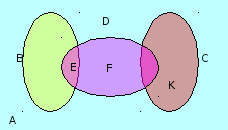
Задача 8.
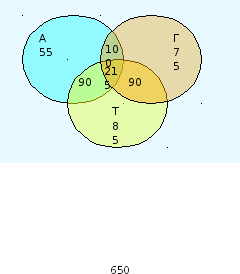
Экзамен по математике содержал 3 задачи: по алгебре, по геометрии и тригонометрии. Из 650 студентов по алгебре решили 400 студентов, по геометрии – 480, по тригонометрии 420 человек. Задачи только по алгебре и геометрии решили 100 человек, только по геометрии и тригонометрии – 90 человек. Сколько студентов решили только одну задачу?
Решение: А – задачи по алгебре, Г – задачи по геометрии, Т – задачи по тригонометрии. По условию: АГ = 100, АТ – 90, Т – 85, Г = 75.
Нам надо найти количество студентов решивших одну задачу, т.е. m (А)+ m (Т) + m (Г), где неизвестно лишь m (А) – количество студентов решивших только алгебру. Из условия геометрию решили 480, следовательно, m (АТГ) = 480 m (Г) – m (АГ) – m (ГТ) = 480-75-100-90 = 215 – количество человек, которые решили все три задачи. Из условия тригонометрию решили 420, следовательно: m (А) = 400 – m (АГ) – m (АТГ) – m (АТ) = 400 – 100 – 215 – 30 = 55 – количество абитуриентов решили только алгебру.
Проверка: итак m (А) + m (Т) + m (Г) = 55 + 85 + 75 = 215 – количество человек, которые решили только 1 задачу. Так как всего 650 студентов, то должно выполниться равенство: 215 + 100 + 30 + 90 + 215 = 650 – верно!
Ответ: 215 человек, которые решили только 1 задачу.
Задача 9.
Учитель математики прочитала нам задачу из раздела круги Эйлера-Венна: по дороге шли два отца и два сына. А всего три человека. Возможна ли такая ситуация и как показать это с помощью кругов Эйлера-Венна?
Р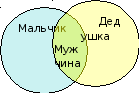 ешение:
ешение:
Отмечу 2 множества: сыновья и отцы. Зная, какие родственные узы бывают, я делаю вывод, что по дороге шел мальчик со своим отцом и дедушкой.
Ответ: По дороге: папа с сыном и своим отцом.
Задача 10: За праздничным столом собрались родственники. Папа объявил, что сегодня у нас в гостях 4 поколения, среди которых 4 мамы, 2 деда и 3 папы, 3 бабушки, 5 детей, а всего 9 человек. Известно, что среди нас 1 прабабушка и только 1 женщина является и мамой, дочкой и внучкой. Как решить данную задачу. Кто собрался за праздничным столом?
Р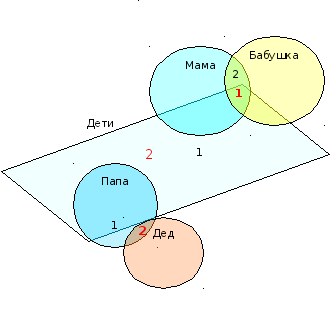 ешение:
ешение:
Ответ: К своей дочери (у неё 2 детей) пришли в гости папа, мама и её бабушка по линии мамы. В гости к её мужу приехали папа и мама.
Сложные задачи
Задача 1. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский (А), немецкий (Н), французский (Ф). 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Решение. При решении данной задачи недостаточно метода «Круги Эйлера-Венна». Удобно применить составление уравнения по условию задачи, а круги Эйлера-Венна в данной задаче наглядно показывают решение.
А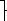
хотя бы 1
+ Н = 34
Ф + Н = 25
Н = 6
По условию: А + Н = на 3 человека , чем Ф + Н = х изучают одновременно 2 языка.
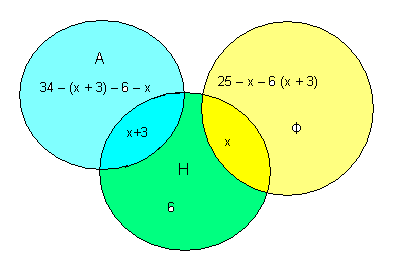
Составим и решим уравнение:
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Ответ: всего 40 человек.
Пример задачи из жизни, которую я нашел в литературе. Данная задача показывает, что с помощью кругов Эйлера-Венна можно решать не только задачи по математике.
Задача 2. Министерство послало в один из лицеев инспектора для проверки, как в нем ведется преподавание иностранных языков. Сотрудник министерства в отчете записал, что в лицее учатся 100 детей. Каждый изучает по крайней мере один из трех языков: французский, немецкий или испанский. Причем все три языка изучают 5 человек; немецкий и испанский 10; французский и испанский 8; немецкий и французский 20; испанский 30, немецкий 23, французский 50. Инспектор, представивший отчет, был уволен. Почему?
Решение: Начнем, как всегда, с обозначений. Назовем Ф множество учащихся, изучающих французский язык, Н – множество учащихся, изучающих немецкий язык, И – тех, кто изучает испанский. В отчете сказано, что каждый из 100 лицеистов изучает хотя бы один из трех языков.
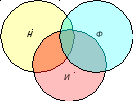
Проверим, соответствует ли это утверждение остальным данным отчета. Их можно записать так: Ф = 50, Н = 23, И = 30, Ф ∩ Н = 20, Ф ∩ И = 8, Н ∩ И = 10, Ф ∩ Н ∩ И = 5. Поскольку множество всех лицеистов есть объединение множеств Ф, Н и И, мощность которого равна 100, то 100 = Ф + Н + И – ( Ф ∩ Н + Ф ∩ И ) + Н ∩ И + Ф ∩ Н ∩ И. Подставим соответствующие значения и получим 50 + 23 + 30 – 20 – 8 – 10 + 5 = 70. Противоречие: 100 ≠ 70. Попробуем из отчета инспектора понять, сколько учеников изучают только немецкий язык. Как следует из рис.5, мощность данного множества равна Н – Н ∩ Ф – Н ∩ И + Н ∩ И ∩ Ф. Подставив соответствующие значения в последнюю формулу, получим 23 – 20 – 10 + 5 = – 2. Опять абсурд! Вывод очевиден – проверка была произведена плохо или совсем не проводилась. Не исключено, что инспектор взял произвольные числа.


 Получите свидетельство
Получите свидетельство Вход
Вход


 еонард Эйлер (1707 - 1783).
еонард Эйлер (1707 - 1783).  еонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Джон Венн — британский логик и философ; основные труды в области логики классов; и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логика, статистика, компьютерные науки.
еонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Джон Венн — британский логик и философ; основные труды в области логики классов; и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логика, статистика, компьютерные науки.

 адача 2. Интересная задача родилась при изучении простых чисел. Даны множества: натуральны, четные и простые числа. Найти пересечение этих множеств.
адача 2. Интересная задача родилась при изучении простых чисел. Даны множества: натуральны, четные и простые числа. Найти пересечение этих множеств.

 ыберите из множества А = {1,5; –7;
ыберите из множества А = {1,5; –7; 


 ешение:
ешение: ешение:
ешение:
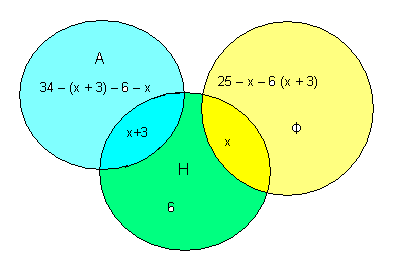










 Материал по математике "Круги Эйлера" (96 КB)
Материал по математике "Круги Эйлера" (96 КB)
 0
0 2850
2850 200
200 Нравится
0
Нравится
0








