«Согласовано» «Утверждаю»
Зам. директора по ВР Директор МОУ СОШ №1
______М.В. Гараган _________ Петранкина Л.М. «___»______2015г. приказ № от 31.08.2015г.
Рабочая программа
кружка «Математика может быть интересной»
для уч-ся 5 классов
учителя математики
Бондаренковой Марии Александровны
Рассмотрено на заседании
педагогического совета
протокол №1
от 28.08.2015 года
2015-16 учебный год
СОДЕРЖАНИЕ ПРОГРАММЫ
1. Пояснительная записка ……………………………………………………..3-4
2. Прогнозируемые результаты освоения Рабочей программы по курсу……5
3. Содержание курса…………………………………………………………....6-7
4. Тематическое планирование с определением основных видов учебной
деятельности…………………………………………………………………...8-18
5. Описание учебно-методического и материально-технического обеспечения
курса по внеурочной деятельности……………………………………………..19
6. Приложения к программе ………………………………………………...20-22
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Математический кружок – одна из наиболее действенных и эффективных форм внеклассной работы по математике. Как известно, устойчивый интерес к математике начинает формироваться в 14-15 лет. Но это не происходит само собой: для того, чтобы ученик в 7 или 8 классе начал всерьёз заниматься математикой, необходимо, чтобы на предыдущих этапах он почувствовал, что размышления над трудными, нестандартными задачами могут доставлять подлинную радость.
Достижению данных целей способствует организация внеклассной работы, которая является неотъемлемой частью учебно-воспитательной работы в школе. Она позволяет не только углублять знания учащихся в предметной области, но и способствует развитию их дарований, логического мышления, расширяет кругозор. Математические кружки по математике являются основной формой внеклассной работы с учащимися в 5-6 классах.
Содержание занятий кружка полностью соответствует требованиям, предъявляемым Федеральным государственным образовательным стандартом (ФГОС) к изучению предметной области «Математика». Занятия математического кружка являются неотъемлемой частью учебного процесса и естественно влияют на улучшение результатов в выполнении требований ФГОС.
Цель – повышение уровня мотивации и развитие устойчивого интереса к изучению математики.
Задачи:
- развитие математических способностей у учащихся и привитие учащимся определенных навыков научно-исследовательского характера;
- воспитание культуры математического мышления;
- развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой;
- расширение и углубление представлений учащихся о практическом значении математики;
- воспитание у учащихся чувства коллективизма и умения сочетать индивидуальную работу с коллективной.
Данная рабочая программа рассчитана на учащихся 5 классов.
Режим занятий: 35 часов в год; 1 час в неделю. Срок реализации программы – 1год.
Оценивание учебных достижений на кружковых занятиях отличается от привычной системы оценивания на уроках. Данная программа предусматривает следующие формы контроля:
- сообщения и доклады (мини);
- тестирование с использованием заданий математического конкурса «Кенгуру»
- творческий отчет (в любой форме по выбору учащихся);
- различные упражнения в устной и письменной форме;
- конкурсы.
Также возможно проведение рефлексии самими учащимися.
Учащимся можно предложить оценить занятие в листе самоконтроля:
| № занятия | Определение уровня трудности занятия | Настроение | Самооценка работы на занятии |
|
| легкое | среднее | трудное |
|
|
ПРОГНОЗИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ РАБОЧЕЙ ПРОГРАММЫ
Занятия в математическом кружке дают возможность обучающимся в 5 классе достичь следующих результатов:
в направлении личностного развития
познавательный интерес, установка на поиск способов решения математических задач;
готовность ученика целенаправленно использовать знания в учении и повседневной жизни для исследования математической сущности предмета (явления события, факта);
способность характеризовать собственные знания, устанавливать какие из предложенных задач могут быть решены;
критичность мышления.
в метапредметном направлении:
способность находить необходимую информацию и представлять ее в различных формах (моделях);
способность планировать и контролировать свою учебную деятельность, прогнозировать результаты;
способность работать в команде, умение публично предъявлять свои образовательные результаты.
в предметном направлении:
способность выявлять отношения между величинами в предметных ситуациях и в ситуациях, описанных в текстах; представлять выделенные отношения в виде различных моделей (знаковых, графических); решать задачи на различные отношения межу величинами;
умение находить рациональные способы вычислений;
умение выявлять и описывать закономерности в структурированных объектах (числовых последовательностях, геометрических узорах и т.п.);
умение изображать точки на плоскости по их координатам и находить координаты точек на плоскости;
умение строить описания геометрических объектов, и конструировать геометрические объекты по их описанию, выполнять простейшие построения циркулем и линейкой;
умение измерять геометрические величины разными способами (прямое измерение, измерение с предварительным преобразованием фигуры, с использованием инструментов, вычисления по формулам);
выполнять сбор информации в несложных случаях, представлять информацию в виде таблиц и диаграмм;
решать удобным для себя способом (в том числе и с помощью таблиц и графов) логические задачи,
СОДЕРЖАНИЕ КУРСА
Раздел 1. Организационное занятие.. (1 час).
Теория. Ознакомление с работой кружка «Математическая шкатулка», необходимость изучение математики, содержание и порядок работы. Знакомство с детьми.
Раздел 2. Из истории математики. (5 часов).
Теория. Ознакомление с историей развития математики, счёта, русскими и советскими учёными – математиками, с древними русскими мерами длины, объёма и денежными единицами.
Практическая часть. Решение задач конкурсных программ.
Форма занятия- теоретические сведения с последующей практической работой.
Раздел 3. Занимательная математика (4 часа)
Теория. Ознакомление с правилами разгадывания математических ребусов и кроссвордов.
Практическая часть. Решение задач-шуток, задач-загадок, математических ребусов, кроссвордов, пословиц и поговорок о числах.
Форма занятия - теоретические сведения с последующей практической работой.
Раздел 4. Наглядная геометрия (12 часов)
Теория. Знакомство с координатной плоскостью. Биография древнегреческого учёного Декарта.
Практическая часть. Задачи на разрезание по линиям клеток. Построение фигур одним росчерком карандаша. Построение фигур по координатам. Рисунки с помощью координат. Игры «Танграм», «Морской бой», с пентамимо. Задачи на вычисление периметров многоугольников, площадей квадратов, прямоугольников и прямоугольных треугольников, объёма различных параллелепипедов, используя готовые модели геометрических фигур.
Форма занятия - теоретические сведения с последующей практической работой.
Раздел 5. Элементы статистики (3 часа)
Теория. Статистические характеристики: среднее арифметическое, мода, размах, медиана, частота.
Практическая часть. Решение задач на вычисление моды, размаха, медианы, частоты и среднего арифметического нескольких полученных данных.
Форма занятия - теоретические сведения с последующей практической работой.
Раздел 6. Логические задачи (4 часа)
Теория. Решение задач с помощью кругов Эйлера. Принцип Дирихле.
Практическая часть. Решение задач на переливание, взвешивание, с помощью кругов Эйлера и на принцип Дирихле.
Форма занятия - теоретические сведения с последующей практической работой.
Раздел 7. Реальная математика (4 часа)
Теория. Задач на части, на скорость, на нахождение числа по его сумме и разности.
Практическая часть. Решение задач реальной математики. Конкурс «Математика в жизни семьи».
Форма занятия- теоретические сведения с последующей практической работой.
Раздел 7. Итоговое занятие (2 часа)
Теория. Математическая газета.
Практическая часть. Выпуск Математической газеты. Конкурсная программа «Математическое кафе».
Форма занятия- теоретические сведения с последующей практической работой.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ С ОПРЕДЕЛЕНИЕМ ОСНОВНЫХ ВИДОВ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ
| № п\п | Наименование раздела, темы | Характеристика деятельности учащихся или виды учебной деятельности | Планируемые результаты | Количество часов | Дата |
| План. | Факт. |
| 1 | Организационное занятие-1 час. Математика вокруг нас. | Личностные: самоопределение, смыслообразование. Регулятивные: целеполагание. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли. Познавательные: поиск и выделение информации. | Умение ясно, точно излагать свои мысли в устной речи, понимать смысл поставленной задачи, выстраивать аргументацию. Приводить примеры и контрпримеры Умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.. | 1 | 4.09.15 |
|
| 2 | Из истории математики-5 часов. 1)История развития математики. 2)История счёта. | Личностные: самоопределение, смыслообразование. Регулятивные: целеполагание. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли. Познавательные: поиск и выделение информации. | Представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации. Развитие представлений о числе и числовых системах от натуральных до действительных чисел. | 1 | 11.09.15 |
|
| 3 | Русские и советские учёные - математики | Личностные: самоопределение, смыслообразование. Регулятивные: целеполагание. Коммуникативные: инициативное сотрудничество в поиске и сборе информации. Познавательные: поиск и выделение информации. | Представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации. Знать русских и советских учёных математиков. | 1 | 18.09.15 |
|
| 4 | Древние русские меры длины, объёма и денежные единицы. | Личностные: самоопределение, смыслообразование. Регулятивные: целеполагание. Коммуникативные: инициативное сотрудничество в поиске и сборе информации. Познавательные: поиск и выделение информации. | Представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации. Знать русские меры длины, денежные единицы | 1 | 25.09.15 |
|
| 5 | Героические эпизоды Великой Отечественной войны в числах и задачах. | Личностные: самоопределение. Регулятивные: контроль, оценка, коррекция. Познавательные: выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. Коммуникативные: управление поведением партнера, контроль коррекция, оценка действий партнера. |
Умение применять изученные понятия, результаты, методы для решения задач практического характера. Умение ясно, точно излагать свои мысли в устной речи, понимать смысл поставленной задачи, выстраивать аргументацию. Приводить примеры и контрпримеры
| 1 | 2.10.15 |
|
| 6 | Из истории замечательных чисел | Личностные: самоопределение, смыслообразование. Регулятивные: целеполагание. Коммуникативные: учебное сотрудничество с учителем и сверстниками Познавательные: логические (установление причинно-следственных связей, построение логической цепи рассуждений | Представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации. Развитие представлений о числе и числовых системах от натуральных до действительных чисел. | 1 | 9.10.15 |
|
| 7 | Занимательная математика-4 часа. Задачи-шутки, задачи-загадки. | Личностные: смыслообразование. Регулятивные: определение последовательных, промежуточных целей с учетом конечного результата. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: моделирование, решение проблемы, построение логических цепей, анализ, умение структурировать знания | Креативность мышления, инициатива, находчивость, активность при решении математических задач. | 1 | 16.10.15 |
|
| 8 | Математические ребусы | Личностные: смыслообразование. Регулятивные: определение последовательных, промежуточных целей с учетом конечного результата. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: моделирование, решение проблемы, построение логических цепей, анализ, умение структурировать знания | Знание математических понятий, определений, фигур, математиков. | 1 | 23.10.15 |
|
| 9 | Математические кроссворды | Личностные: смыслообразование. Регулятивные: определение последовательных, промежуточных целей с учетом конечного результата. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: моделирование, решение проблемы, построение логических цепей, анализ, умение структурировать знания | Знание математических понятий, определений, фигур, математиков | 1 | 30.10.15 |
|
| 10 | Пословицы и поговорки с числами | Личностные: смыслообразование. Регулятивные: определение последовательных, промежуточных целей с учетом конечного результата. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: моделирование, решение проблемы, построение логических цепей, анализ, умение структурировать знания | Умение находить в различных источниках необходимую информацию. | 1 | 13.11.15 |
|
| 11 | Наглядная геометрия-12 часов. Задачи на разрезание по линиям клеток. Равные фигуры. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Умение изображать геометрические фигуры на клетчатой бумаге. Умение изображать равные фигуры, симметричные фигуры. | 1 | 20.11.15 |
|
| 12 | Построение фигур одним росчерком карандаша. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Умение изображать геометрические фигуры и их конфигурации на плоскости от руки и с помощью чертёжных инструментов
| 1 | 27.11.15 |
|
| 13 | Координатная плоскость | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Умение иллюстрировать понятие декартовой системы координат. Умение изображать точки на координатной плоскости по координатам. Умение записывать координаты точек, изображённых в системе координат. | 1 | 4.12.15 |
|
| 14 | Построение фигур по координатам. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Умение изображать точки и фигуры на координатной плоскости по координатам. Умение определять координаты точек, изображённых в системе координат. | 1 | 11.12.15 |
|
| 15 | Рисуем с помощью координат. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Умение изображать точки и фигуры на координатной плоскости по координатам. Умение определять координаты точек, изображённых в системе координат. | 1 | 18.12.15 |
|
| 16 | Геометрия на спичках | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Знание римской системы записи чисел, свойств геометрических фигур. | 1 | 25.12.15 |
|
| 17 | Геометрические фигуры. Игра «Танграм» | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Исследовать и описывать свойства плоских геометрических фигур, используя эксперимент и наблюдения. Моделировать геометрические объекты, используя геометрические фигуры игры танграм. | 1 | 15.01.15 |
|
| 18 | Игра «Морской бой» | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Изображать геометрические фигуры на клетчатой бумаге. Изображать равные фигуры, симметричные фигуры. | 1 | 22.01.15 |
|
| 19 | Игры с пентамимо. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Моделировать геометрические объекты, используя геометрические фигуры игры пентамимо. Изображать геометрические фигуры на клетчатой бумаге. Изображать равные фигуры, симметричные фигуры. | 1 | 29.01.15 |
|
| 20 | Задачи на разрезание геометрических фигур. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Умение изображать геометрические фигуры на клетчатой бумаге. Умение изображать равные фигуры, симметричные фигуры. | 1 | 5.02.15 |
|
| 21 | Задачи на вычисление периметров многоугольников, площадей квадратов, прямоугольников и прямоугольных треугольников. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Распознавать на чертежах, рисунках и моделях плоские геометрические фигуры. Измерять с помощью линейки длины отрезков. Выражать одни единицы измерения длин через другие. Вычислять периметры многоугольников, площади квадратов и прямоугольников, используя формулы. | 1 | 12.02.15 |
|
| 22 | Задачи на нахождение объёма различных параллелепипедов. | Личностные: самоопределение Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Коммуникативные: учебное сотрудничество с учителем и сверстниками | Распознавать развёрстки куба, параллелепипеда. Вычислять объёмы куба и параллелепипеда, используя формулы. Выражать одни единицы объёма через другие. | 1 | 19.02.15 |
|
| 23 | Элементы статистики-3 часа. Статистические характеристики: среднее арифметическое, мода, размах | Личностные: смыслообразование. Регулятивные: планирование, контроль, оценка, коррекция, выделение и осознание того .что еще подлежит усвоению Коммуникативные: инициативное сотрудничество в поиске и сборе информации. Познавательные: поиск и выделение информации; | Извлекать информацию из таблиц, диаграмм, выполнять вычисления по табличным данным, сравнивать величины, находить наибольшие и наименьшие. Выполнять сбор информации, организовывать информацию в виде таблиц и диаграмм. | 1 | 26.02.15 |
|
| 24 | Статистические характеристики: медиана, частота | Личностные: смыслообразование. Регулятивные: планирование, контроль, оценка, коррекция, выделение и осознание того .что еще подлежит усвоению Коммуникативные: инициативное сотрудничество в поиске и сборе информации. Познавательные: поиск и выделение информации; | Извлекать информацию из таблиц, диаграмм, выполнять вычисления по табличным данным, сравнивать величины, находить наибольшие и наименьшие. Выполнять сбор информации, организовывать информацию в виде таблиц и диаграмм. | 1 | 4.03.15 |
|
| 25 | Элементы статистики. Практическое занятие. | Личностные: смыслообразование. Регулятивные: планирование, контроль, оценка, коррекция, выделение и осознание того .что еще подлежит усвоению Коммуникативные: инициативное сотрудничество в поиске и сборе информации. Познавательные: поиск и выделение информации; | Извлекать информацию из таблиц, диаграмм, выполнять вычисления по табличным данным, сравнивать величины, находить наибольшие и наименьшие. Выполнять сбор информации, организовывать информацию в виде таблиц и диаграмм. | 1 | 11.03.15 |
|
| 26 | Логические задачи-4 часа. Задачи на переливание | Личностные планирование учебной деятельности Регулятивные: целеполагание, прогнозирование; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий | Осмысливать текст задачи, извлекать необходимую информацию, строить логическую цепочку рассуждений, критически оценивать полученный результат. | 1 | 18.03.15 |
|
| 27 | Логические задачи. Задачи на взвешивание | Личностные планирование учебной деятельности Регулятивные: целеполагание, прогнозирование; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий | Осмысливать текст задачи, извлекать необходимую информацию, строить логическую цепочку рассуждений, критически оценивать полученный результат. | 1 | 25.03.15 |
|
| 28 | Логические задачи. Решение задач с помощью кругов Эйлера | Личностные планирование учебной деятельности Регулятивные: целеполагание, прогнозирование; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий | Осмысливать текст задачи, извлекать необходимую информацию, строить логическую цепочку рассуждений, критически оценивать полученный результат. | 1 | 8.04.15 |
|
| 29 | Логические задачи. Принцип Дирихле. | Личностные планирование учебной деятельности Регулятивные: целеполагание, прогнозирование; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий | Осмысливать текст задачи, извлекать необходимую информацию, строить логическую цепочку рассуждений, критически оценивать полученный результат. | 1 | 15.04.15 |
|
| 30 | Реальная математика-4 часа. Задачи на части | Личностные планирование учебной деятельности Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера. Регулятивные: контроль, оценка, коррекция. Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. | Осмысливать текст задачи, извлекать необходимую информацию, строить логическую цепочку рассуждений, критически оценивать полученный результат. | 1 | 22.04.15 |
|
| 31 | Задачи на нахождение чисел по их сумме и разности | Личностные планирование учебной деятельности Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера. Регулятивные: контроль, оценка, коррекция. Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. | Осмысливать текст задачи, извлекать необходимую информацию, строить логическую цепочку рассуждений, критически оценивать полученный результат. | 1 | 29.04.15 |
|
| 32 | Задачи на скорость | Личностные планирование учебной деятельности Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера. Регулятивные: контроль, оценка, коррекция. Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. | Использовать знания о зависимости между величинами (скорость, время, расстояние) при решении текстовых задач. | 1 | 6.05.15 |
|
| 33 | Конкурс «Математика в жизни семьи» | Личностные: самоопределение. Регулятивные: контроль, оценка, коррекция. Познавательные: выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. Коммуникативные: управление поведением партнера, контроль коррекция, оценка действий партнера. | Умение применять изученные понятия, результаты, методы для решения задач практического характера.
| 1 | 13.05.15 |
|
| 34 | Итоговое занятие Выпуск газеты «Математика может быть интересной». | Личностные: самоопределение. Регулятивные: контроль, оценка, коррекция. Познавательные: выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. Коммуникативные: управление поведением партнера, контроль коррекция, оценка действий партнера. |
| 1 | 20.05.15 |
|
| 35 | Конкурсная программа «Математическое кафе» | Личностные: самоопределение. Регулятивные: контроль, оценка, коррекция. Познавательные: выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. Коммуникативные: управление поведением партнера, контроль коррекция, оценка действий партнера. | Креативность мышления, инициатива, находчивость, активность при решении математических задач. | 1 | 27.05.15 |
|
ОПИСАНИЕ УЧЕБНО-МЕТОДИЧЕСКОГО И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОГО ОБЕСПЕЧЕНИЯ КУРСА ПО ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ
Список литературы для учителя:
А.В. Фарков. Внеклассная работа по математике. – Москва «Айрис-пресс» 2013г;
Шарыгин И.Ф., Шевкин А.В. Математика. Задачи на смекалку 5-6 классы.- М.: «Просвещение», 2013г;
Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка 5-6 классы.- М.: «Издательство НЦ ЭНАС», 2012г;
«Наглядная геометрия. 5-6 кл.: пособие для общеобразовательных учреждений»/ И.Ф. Шарыгин, Л.Н. Ерганжиева.-М.: Дрофа, 2013.
Медиаресурсы:
1.http://www.edu.ru - Федеральный портал «Российское образование»;
2.http://videouroki.net- полезные материалы для учителя.
Список литературы для учащихся:
1.«Наглядная геометрия. 5-6 кл.: пособие для общеобразовательных учреждений»/ И.Ф. Шарыгин, Л.Н. Ерганжиева.-М.: Дрофа, 2013;
Б.А. Кордемский. Математическая смекалка. – Изд. Физико-математическая литература. 2010г;
Л.М. Лоповок. Математика на досуге. – Издательство «Просвещение».2013 г.
ПРИЛОЖЕНИЯ К ПРОГРАММЕ
Разработки отдельных игр, бесед, конкурсов, занятий.
Методической особенностью изложения учебных материалов на кружковых занятиях является такое изложение, при котором новое содержание изучается на задачах. Метод обучения через задачи базируется на следующих дидактических положениях:
• наилучший способ обучения учащихся, дающий им сознательные и прочные знания и обеспечивающий одновременное их умственное развитие, заключается в том, что перед учащимися ставятся последовательно одна за другой посильные теоретические и практические задачи, решение которых даёт им новые знания;
• с помощью задач, последовательно связанных друг с другом, можно ознакомить учеников даже с довольно сложными математическими теориями;
• усвоение учебного материала через последовательное решение задач происходит в едином процессе приобретения новых знаний и их немедленного применения, что способствует развитию познавательной самостоятельности и творческой активности учащихся.
Большое внимание уделяется овладению учащимися математическими методами поиска решений, логическими рассуждениями, построению и изучению математических моделей. Примерами таких методов служат принцип Дирихле, круги Эйлера, графы и др.
«Математика вокруг нас». (Презентация)
А для чего, ребята, мы сегодня собрались? Для того, чтобы никто из вас не задавал такой знакомый всем учителям математики вопрос: «А зачем мне математика? Мне она в жизни не пригодится». Слово «математика» пришло к нам из древнего языка: произошло от древнегреческих слов «математика» и «матема» - «познание, наука». Математика - наука о количественных отношениях и пространственных формах действительного мира. И если есть упражнения для развития тела, то математика призвана развивать логическое мышление, внимание, тренировать мозг. Недаром ее называют «гимнастикой ума».
Я хочу, чтобы вы убедились, что математика - чудесная, не сухая наука и что заниматься ею очень увлекательно.
Итак, мы начинаем .
Ребята, в жизни вы не встретите ни одного человека, который не занимался бы математикой. Каждый из нас умеет считать, знает таблицу умножения, умеет строить геометрические фигуры. С этими фигурами мы часто встречаемся в окружающей жизни.
Кто-то из вас, возможно, думает, что различные замысловатые линии и поверхности можно встретить только в книгах учёных математиков. Однако это не так. Стоит внимательно присмотреться, и мы сразу обнаружим вокруг нас всевозможные геометрические фигуры. Оказывается, их очень много, просто раньше мы их не замечали. Вот комната. Все её стены, пол и потолок являются прямоугольниками, а сама комната - параллелепипед.
Посмотрите на паркетный пол. Плитки паркета - квадраты, прямоугольники или правильные шестиугольники.
Мебель в комнате - тоже комбинация геометрических тел. Стол -плоский параллелепипед, лежащий на двух других параллелепипедах - тумбочках, в которых есть ящики. Лампа с абажуром в форме усечённого конуса или в форме полусферы и т.д.. Ведро либо цилиндрической формы, либо - усечённый конус, либо - клнус.
Гранёный стакан, он имеет форму многогранной усечённой пирамиды. Воронка состоит из конуса и цилиндра. Нальём в стакан воду, поверхность воды имеет форму круга. Наклоним стакан, чтобы вода не вылилась. Тогда край водной поверхности станет эллипсом.
Выйдем на улицу. Перед нами дома. Сам дом - призма, а его стены - плоскости. Колонны у дома - это цилиндры.
В Москве - Кремль. Прекрасны его башни и стены! Сколько геометрических фигур положено в их основу!
По улице движутся автомобили. Их колёса - круги. Сядем в поезд. Станция далеко позади. Но и здесь геометрия не покидает нас. Вдоль дороги на столбах натянуты провода - это прямые линии, а столбы - это перпендикуляры к земле. Вот линия высоковольтной передачи, провода от собственной тяжести слегка провисают к земле, а зимой же они, наоборот, натягиваются, так как металл от холода сжимается. Вопросом определения необходимой длины такого провода для передачи на большие расстояния занимается математика.
Очень часто мы встречаемся с шаровой поверхностью: шариковые подшипники, резервуары для хранения газа, - их делают шаровой или цилиндрической формы, так как при этом расходуется меньше металла. Мы живём на земном шаре, хотя в действительности форма земли не шар, а более сложное тело - «эллипсоид вращения». У полюсов оно сплюснутое, отношение малой оси к большой составляет 299/300. Это не много, но эту величину приходится учитывать при составлении географических карт.
Во многих случаях наблюдения над явлениями природы помогают человеку в решении его технических задач. Так, на заре развития авиации наши знаменитые учёные Н. Е. Жуковский (отец русской авиации) и С. А. Чаплыгин (один из основоположников аэродинамики) исследовали полёт птиц, чтобы сделать выводы относительно наивыгоднейшей формы крыла самолёта и условий его полёта.
Мы идём в магазин. Чтобы сделать покупку, мы решаем в уме задачу с данными: цена, количество, стоимость. Мы едем в путешествие и решаем для себя задачу с данными: скорость, время, расстояние. Экономисты на заводе каждый день решают массу задач с данными: работа, производительность труда, время. Инженер или техник на производстве решает задачи на «Сопротивления материалов».
Например:
Балка в технике - это металлический или деревянный брус. На них держится вес перекрытий и предметов, находящихся в здании. Если вес большой, то балки могут не выдержать и здание может рухнуть. Поэтому до постройки здания надо сделать экономические расчёты и выяснить материал, форму, размер балки, чтобы она выдержала конструкцию.
Зная формулы о силе трения, инженер может рассчитать, каким канатом можно удержать на пристани корабль (канат закидывается за столб на пирсе).
Зная специальные формулы, врач-криминалист может рассчитать время, когда умер человек.
Много трудных математических задач приходится решать в теории космических полётов. Одной из них является задача об определении количества топлива для того, чтобы придать ракете нужную скорость. Математики нашли способ уменьшения количества этого топлива, т. е. при меньшей затрате горючего ракета может улететь дальше.
Благодаря математике появились вычислительные счетные машины (компьютеры). Вычислительная техника прошла путь от простых счётов, арифмометров, логарифмических линеек до микрокалькуляторов и компьютеров. Сейчас вычислительные машины используются во всех отраслях народного хозяйства: в статистике, торговле, автоматизированном управлении заводами и фабриками. Машины не только считают, они могут делать переводы с одного языка на другой, могут сочинять музыку, играть в шахматы.
Чтобы производить такие машины или пользоваться ими, нужно изучать высшую математику, а для её изучения нельзя обойтись без хороших знаний элементарной математики. Учить математику надо каждый день, потому что новые знания всегда опираются на старые. Нельзя оставлять неразобранной ни одной задачи и примера. Если не разобрался сам, спроси товарища или учителя. Знай, что если сегодня ты не понял немножко, то завтра не поймёшь многое.
Истории развития математики (Презентация)
Вступительное слово: Ребята, сегодня мы с вами отправимся в путешествие по страницам истории математики. Каждый день на уроках математики вы узнаете о свойствах чисел и фигур, решаете задачи, а вернувшись домой, повторяете изученный материал и делаете домашнее задание. Большим помощником для вас является учебник. О многом можно узнать из учебника: как складывать и вычитать числа, решать уравнения и задачи. Но про то, кем и когда были придуманы числа, как впервые люди познакомились с геометрическими фигурами, - про все это в учебнике сказано очень мало. Не говорится в учебнике и о том, как и где, применяют математику в окружающем нас мире. И на этом уроке, мы постараемся заглянуть в этот удивительный мир. А для этого нам надо вернуться на несколько веков назад.
Цель
Знакомство с историей развития математики;
С ее ролью в жизни человека.
Пробудить интерес учащихся к математике.
Как люди научились считать.
Никто не знает, когда впервые появились счет и число. Но уже несколько десятков тысяч лет назад люди собирали плоды и ягоды, охотились на диких животных, ловили рыбу, делали каменные ножи и топоры. И им надо было знать, хватит ли добычи до следующей охоты, много ли поймано рыбы, надо было делить собранные плоды.
Еще не умея считать, древний охотник знал, все ли собаки вышли с ним на охоту или какая - нибудь убежала. Люди знали, что у человека столько же рук, сколько рогов у оленя, сколько крыльев у птицы. Они научились считать до двух. А все, что шло после двух, называлось « много».
Но потом понадобилось называть и другие числа. Ведь и собак у охотника, и стрел у него, и овец у пастуха может быть больше чем две. Чем многочисленнее становились их стада, тем большие числа становились им нужны. И старые методы счета вытеснил новый – счет по пальцам. Пальцы оказались прекрасной вычислительной машиной. С их помощью можно было сосчитать до 5, а если взять две руки, то и до 10. Тогда этого практически хватало для большинства потребностей людей.
А научившись считать по пальцам до десяти, люди сделали следующий шаг вперед и стали считать десятками.
Вопрос: «Когда, вы, впервые познакомились с математикой?
Практическое задание.
( С помощью пальцев рук ответить на следующие вопросы.)
Какую оценку в школе вы хотели бы получать на уроках?
Сколько человек в вашей семье?
Сколько вам лет?
Из науки о числах.
Появились числа. Каждое число имело свое « имя» и свою символику. Появилась потребность выполнять действия над ними, чтобы решать сложные задачи, встречавшиеся в практической деятельности, пришлось, кроме натуральных чисел, придумать другие числа – обыкновенные, десятичные дроби, отрицательные числа, научиться использовать пропорции, а потом создать новую науку – алгебру, позволявшие решать любые задачи.
Первые единицы длины.
Научились люди считать, теперь им надо было научиться измерять. Ведь без измерений нельзя ни сшить платье, ни узнать который час, а так как люди жили большими группами, начался обмен товарами перешедший потом в торговлю, возникли первые государства. Царские писцы должны были знать, какова площадь поля, купцы длину продаваемой ткани. Тогда появилась нужда в измерениях. В древности длины измеряли локтями, длиной ступни, длинами зерен.
В каждой стране была своя система мер. В эпоху раздробленности Руси не было единой системы мер. В ХV и ХVI веках происходит объединение русских земель. С возникновением и ростом общегосударственной торговли и с установлением для казны сборов со всего населения объединенной страны встает вопрос о единой системе мер для всего государства.
Прежняя русская система мер длины, дополненная новыми мерами, получила окончательный вид.
Вопрос. Назовите систему мер длины, которую мы сейчас используем.
Практическое задание. (выполняется в рабочей тетради)
Перевести данные меры длины, в меры, используемые в настоящее время.
Геометрия и геометрические фигуры.
Без измерений не могли обойтись и древние строители дворцов и храмов. Ученые, изучавшие древние постройки, нашли много рисунков, украшавших их полы и стены. Полы дворцов часто складывали из мраморных плит различной формы или дощечек. Сами того не зная, они занимались геометрией.
Как возникла геометрия.
Когда первобытные люди делали посуду из глины, они украшали ее узорами. Сначала эти узоры были очень простыми, а потом они все усложнялись и превращались в орнаменты, составленные из геометрических фигур.
С геометрическими фигурами имели дело и кожевник, резавший кожу, и кузнец, ковавший железные изделия, и портной, разрезавший ткань на куски.
Крестьяне измеряли собранный урожай корзинами, а корзины имели различную форму и разные объемы, поэтому надо было уметь измерять объем корзины.
С геометрическими фигурами имели дело и землемеры. В Древнем Египте все земледелие было сосредоточено на очень узкой полосе земли - в долине реки Нил. Земли было мало, и каждый крестьянин очень дорожил своим участком. Каждую весну Нил разливался и удобрял землю плодородным илом. Но при разливе смывались знаки, указывающие границы участков, и потом приходилось снова восстанавливать эти границы.
Так появились первоначальные сведения о геометрических фигурах.
По мере того как усложнялось ремесло, совершенствовались знания.
Строителям храмов, дворцов и пирамид надо было знать, какой будет объем пирамиды, сколько пойдет на неё камня, сколько класть каменных плит в каждый слой пирамиды. А чтобы здание не рушилось, надо было возводить стены вертикально, под прямым углом к поверхности земли.
Знания о фигурах записывали в книги, передавали их от одного поколения писцов и строителей другому. Возникла наука об измерении площадей и объемов, о различных геометрических фигурах. ( Геометрия – наука об измерении земли).
Вопрос: Какие геометрические фигуры вы знаете?
Практическое задание:
Назовите геометрические фигуры, которые вы здесь видите?
Математические игры.
Игра в 15
Изобретатель этой головоломки американец Сэмюель Ллойд назначил за ее решение крупную денежную премию. Многие люди, надеясь ее получить, целыми днями не отрывались от игры. Но никому не удавалось расположить шашки по порядку. Предложенная задача была неразрешима. Сам Ллойд не умел этого доказывать. И только вмешательство математиков прояснило дело.
Математические головоломки.
Практическое задание.
Расставьте цифры от 1 до 9 так, чтобы сумма их по любой прямой, проходящей через центр, равнялась 15.
Машины – математики.
Много веков люди мечтали люди создать машины, которые бы сами выполняли порученные им работы. Чтобы создать такие автоматы, понадобились машины, умеющие выполнять арифметические операции.
Вопрос: Какие «машины – математики» вы можете назвать?
15 слайд (по щелчку.)
Итог урока.
Вот и закончилась наше путешествие в мир математики.
А, теперь, давайте с вами подведем итог нашего урока.
Что нового вы узнали? Какую роль играет в нашей жизни математика?
Сидя за письменным столом, рождались открытия великих ученых – математиков, без которых сегодня бы не взлетали ракеты, и не возник бы мир техники.
Вопрос: А вы сможете назвать фамилии математиков, и чем они знамениты?
Сообщение: С.В.Ковалевская.
Русские и советские учёные математики
Ковалевская
Софья Михайловна
(1850-1891)
Выдающаяся женщина – математик. Она была первой женщиной, чьи научные заслуги были оценены столь высоко. Научные труды Софьи Ковалевской явились важным вкладом в мировую науку и не потеряли своей ценности до настоящего времени.
Киселёв
Андрей Петрович
(1852 – 1940)
Русский педагог - математик, автор популярнейших учебников по математике, по которым обучались несколько поколений школьников в дореволюционной России и в Советском Союзе. издал в 1884 г. учебник «Математический курс арифметики для средних учебных заведений», в 1888 г. учебник «Элементарная алгебра», в 1893 г. учебник «Элементарная геометрия» выдержал около полусотни изданий
Лобачевский
Николай Иванович
(1792 - 1856)
Великий русский математик. Многие математики бились над доказательством пятого постулата Евклида, и только наш русский учёный сделал гениальное открытие о независимости пятого постулата от других. На основании этого Лобачевский доказал, что можно построить другую геометрию, отличную от геометрии Евклида. Такая геометрия называется геометрией Лобачевского.
Магницкий
Леонтий Филиппович
(1669 - 1739)
Известный русский просветитель – математик, автор первого печатного учебника математики в России, изданного в 1703 г. был выходцем из тверских крестьян, благодаря своему таланту и трудолюбию сумел добиться уважения и признания современниками. Он имел личные беседы с Петром Первым. Ломоносов высоко оценил «Математику» Магницкого. Эта книга имела огромное значение для развития математики в России.
Марков
Андрей Андреевич
(1856 - 1922)
Выдающийся русский математик, внёсший большой вклад в теорию вероятности, математический анализ и теорию чисел. Последователь П. Л. Чебышева. Как и все выдающиеся русские математики, А. А. Марков занимался многими проблемами математического анализа. В общем списке его научных трудов работы по математическому анализу составляют более одной третьей части.
Остроградский
Михаил Васильевич
(1801-1881)
выдающийся русский математик. Занимался математическим анализом, алгеброй, теорией чисел, прикладными науками. Составил замечательные учебники по высшей и элементарной математике, вёл большую педагогическую деятельность. М. В. Остроградский был одним из тех учёных, которые прославили русскую науку девятнадцатого века.
Колмогоров
Андрей Николаевич
(1903-1987)
советский математик, Научную деятельность начал в области теории функций действительного переменного, где ему принадлежат фундаментальные работы по тригонометрическим рядам, теории меры, теории множеств, теории интеграла, теории приближения функций. внес существенный вклад в разработку конструктивной логики, топологии, теории дифференциальных уравнений, функционального анализа. Основополагающее значение имеют работы в области теории вероятностей.
Чебышев
Пафнутий Львович
(1821-1894)
выдающийся русский математик и механик, его исследования, получившие мировое признание, относятся к теории приближения функции многочленами, интегральному исчислению, теории вероятности, теории механизмов. Имя п. л. Чебышева увековечено в таких математических понятиях, как закон Чебышева, неравенство Чебышева.
Древние русские меры длины и денежные единицы (Презентация)
Пядь употреблялась и в народных пословицах. Говорят:
«Семь пядей во лбу» - когда хотят сказать об очень умном человеке
Аршин - длина руки от плеча до конца среднего пальца
Говорят:
«Видит на три аршина под землю» -
об очень проницательном человеке
Локоть
Говорят:
«Близок локоть да не укусишь»,
« Близок локоток, да ум короток» - о каком-нибудь простом, но невыполнимом деле
Шаг
Своя мера длины как шаг выразилась в народных пословицах и поговорках. Говорят:
« Шагнул и царство покорил», « Ни шагу назад»,
т. е. не отступать
Сажень
Различали два вида сажени: маховая и косая
косая сажень - расстояние от первого пальца левой стопы до концевой фаланги среднего пальца поднятой правой руки, около 248 см.
маховая сажень расстояние между концами пальцев распростёртых рук,
около 1м 76 см.
Верста
При Петре Первом была введена верста длиной в 500 саженей. На таком расстоянии друг от друга вдоль наиболее важных дорог ставили столбы, окрашенные в три цвета. Отсюда название «столбовая дорога» для хорошего наезженного пути. В начале XIX в. Вдоль основных дорог государства Российского появились черно-белые полосатые столбы, на которых отмечались расстояния в верстах
Перст
сначала так называли именно указательный палец, его ширина около 2 см. Отсюда происходит анатомический термин «двенадцатиперстная кишка»
Вершок
Наименование "Вершок" происходит от слова "верх". При определении роста человека или животного счёт велся после двух аршин (обязательных для нормального взрослого человека): если говорилось, что измеряемый был 15 вершков роста, то это означало, что он был 2 аршина 15 вершков, т.е. 209 см.
На уроке математике в 7-й группе присутствовали учащиеся, у которых было 56 ушей, у учительницы на 54 уха меньше. Сколько всего ушей можно насчитать во время урока математики?
Задачи-шутки
Площадь одного уха слона равна 10 000 кв.см. Узнай, в кв. м., площадь 2 ушей слона..
Допустим, что ты решил прыгнуть в воду с высоты 8 метров. И, пролетев 5 метров, передумал. Сколько метров придется тебе еще лететь поневоле?
Младенец Кузя орет как резаный 5 часов в сутки. Спит, как убитый 16 часов в сутки. Остальное время младенец Кузя радуется жизни всеми доступными ему способами. Сколько часов в сутки младенец Кузя радуется жизни?
Голодный Вася съедает за 9 мин. 3 батончика, сытый Вася тратит на 3 бат. 15 мин. Насколько мин. быстрее управляется с одним батончиком голодный Вася?
У младенца Кузи еще 4 зуба, а у его бабушки только 3. Сколько зубов у бабушки и внука?
Кто окажется тяжелее после ужина: первый – людоед, который весил до ужина 48 кг и на ужин съел 2-го людоеда или второй, который весил 52 кг и съел первого.
У осьминога 8 ног. Тремя парами ног он крепко держит трех водолазов. Сколько ног бездельничали у осьминога?
Пожарных учат надевать штаны за три секунды. Сколько штанов успеет надеть хорошо обученный пожарный за 1 минуту?
В бублике одна дырка, а в кренделе в 2 раза больше. На сколько меньше дырок в 7 бубликах, чем в 12 кренделях?
10 Если младенца Кузю взвесить вместе с бабушкой – получится 59 кг. Если взвесить бабушку без Кузи – получится 54 кг. Сколько весит Кузя без бабушки?
11 Боксер, каратист, штангист погнались за велосипедистом со скоростью 12 км/ч. Догонят ли они велосипедиста, если тот, проехав 45 км со скоростью 15 км/ч, приляжет отдохнуть на часок?.
12 Рост Кати 1 м 75 см. Вытянувшись во весь рост, она спит под одеялом, длина которого 155 см. Сколько сантиметров Кати торчит из-под одеяла?.
13. Сколько дырок окажется в клеенке, если во время обеда 12 раз проткнуть ее вилкой с 4 зубчиками?.
Построение фигур одним росчерком карандаша
Цель:
Задачи:
активизировать мышление обучающихся в процессе разрешения специально созданной проблемной ситуации;
развивать устойчивый интерес обучающихся к математике и ее приложениям;
расширять и углублять представления обучающихся о практическом значении математики;
развивать математический кругозор, творческие способности обучающихся.
Ход занятия
1. Постановка проблемной ситуации.
Не отрывая карандаш от бумаги, и не проводя по одной линии дважды, начертить «открытый конверт» (рис. 1).

Рис.1
2. Объяснение нового материала.
Для решения задач, подобных этой, существуют признаки, по которым заранее несложно установить, можно ли данную фигуру начертить одним росчерком или нет. Если можно, то с какой точки следует начинать вычерчивание? Изучением этих признаков и их обоснованием занимается наука топология.
Топология - раздел математики, изучающий такие свойства фигур, которые не меняются при любых деформациях, производимых без разрывов и склеиваний.
С точки зрения топологии, например, полноторий, круг, эллипс, квадрат и треугольник обладают одинаковыми свойствами и являются по сути одной и той же фигурой.
Условимся называть точки, в которых сходится четное количество линий, четными, а точки, в которых сходится нечетное число линий, - нечетными. Например, у «открытого конверта» две нижние вершины являются нечетными, а остальные - четные.
Получаем следующие
признаки вычерчивания фигур одним росчерком:
а) если нечетных точек в фигуре нет, то ее можно начертить одним росчерком, начиная вычерчивать с любого места;
б) если в фигуре две нечетные точки (если фигура имеет нечетную точку, то она всегда имеет и вторую нечетную точку), то ее можно начертить одним росчерком, начав вычерчивание в одной из нечетных точек и закончив в другой;
в) если в фигуре более двух нечетных точек, то ее нельзя вычертить одним росчерком.
Например, «открытый конверт» можно начертить непрерывной линией, т. е. не отрывая карандаша от бумаги, так как у него две нечетных вершины; начинать вычерчивание необходимо в одной из нечетных вершин.
3. Упражнения на закрепление
а) Вычерчивание фигур
1). Определите, какие из фигур, изображенных на рис. 2 можно начертить, не отрывая карандаш, от бумаги (и не проводя по одной линии дважды).
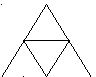
Ответ: а) можно, б) нельзя, в) можно, г) можно, д) можно, е) можно, ж) можно.



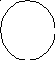

а)
б)
г)
в)
е)
ж)


д)
Рис. 2
2). Нарисуйте те фигуры (см. рис. 2), которые можно начертить одним росчерком.
Физминутка.
Рисуй глазами треугольник.
Теперь его переверни вершиной вниз.
И вновь глазами по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально.
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!
б) Решение задач
3). Только что приобретенные вами знания имеют порой любопытное применение. Великий математик Л. Эйлер в 1736 г. занимался решением такой своеобразной задачи:
В Кенигсберге река, омывающая два острова, делится на два рукава, через которые перекинуто семь мостов (рис. 3). Можно ли обойти все эти мосты, не побывав ни на одном из них более раза?
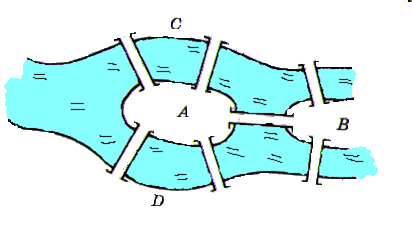
Рис. 3
Решение.
Составим схему к решению задачи (рис.4). Из рисунка видно, что у полученной фигуры четыре нечетные вершины, следовательно, ее нельзя построить, не пройдя по одной линии дважды, а значит, нельзя пройти по мостам так, чтобы не пройти по одному и тому же два раза.
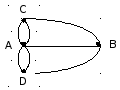
Рис. 4
4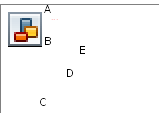 ). Решите задачу с девятью мостами, аналогичную предыдущей по условию и требованию (рис 5).
). Решите задачу с девятью мостами, аналогичную предыдущей по условию и требованию (рис 5).
Рис. 5
Решение.
Составим схему, аналогичную предыдущей задаче (рис. 6). Из рисунка видно, что у полученной фигуры две нечетные вершины, следовательно, ее можно построить, не отрывая карандаша от бумаги, а значит, можно пройти по мостам, не пройдя по одному и тому же два раза, начиная, например, с одного из мостов островка Е.

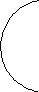








А
В
С
D
E
Рис.6
4. Домашняя работа
1). Начертить фигуры, изображенные на рис. 7, одним росчерком карандаша (там, где это возможно), предварительно определив, возможно ли это.










б)
в)
а)
Рис. 7
Ответ: а) Можно; б) можно; в) можно.
2). Через реку, омывающую шесть островов, перекинуто семнадцать мостов (рис. 8). Можно ли обойти все эти мосты, не побывав ни на одном из них более одного раза?
A
С
D
B
G
Е
Н
F
Рис. 8
Решение.
Составим схему (рис. 9). Из рисунка видно, что у полученной фигуры две нечетные вершины, следовательно, ее можно построить одним росчерком карандаша, а значит, можно пройти по всем мостам, побывав на каждом из них не более одного раза, начиная, например, с моста на острове В.
Рис. 9
Математические игры
| Танграм (в переводе с китайского "Семь дощечек мастерства") - головоломка, состоящая из семи плоских фигур, из которых необходимо сложить другую фигуру. При этом обязательно использовать все 7 фигур, и перекрывания фигур не допускается. История появления танграма Наиболее распространенной версией появления игры "Танграм" является версия, созданная С. Лойдом и описанная им в книге "Восьмая книга Тана" (1903г.). По вымышленной версии С. Лойда игра-головоломка насчитывает около 4000 лет, а изобрело эту головоломку божество по имени Тан. Книга содержит 700 задач, правда некоторые из них не разрешимы.
Есть такая версия: более 4000 тысяч лет назад у строителя из рук выпала фарфоровая плитка и разбилась на семь частей. Он в спешке, расстроенный, старался сложить ее, но каждый раз получал не квадрат. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости.
Появление игры иногда связывают с легендой. Около 2,5-ой тысяч лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по годам, но не хотел учиться. Мальчик играл только игрушками, познания наук его не интересовали. Поэтому император позвал к себе трех мудрецов, которые были художником, математиком и философом. Император велел им придумать игру, играя в которую, наследник изучил начала математики, научился смотреть на мир пристальными глазами художника и стал бы терпеливым, как истинный философ, При этом понял, что зачастую сложные вещи состоят из простых вещей. Подумав некоторое время, три мудреца представили императору игру "Ши-Чао-Тю"- квадрат, разрезанный на семь частей.
Многие считают, что танграм появился во времена правления династии Мин от вида мебели яньцзиту, которая зародилась в империи Сун, но первое упоминание о нём встречается в китайской книге 1813-го года во время правления императора Цзяцина. Появление на западе относят к началу XIX века, когда в 1802 году китайцы подарили сыну американского судовладельца подарили танграм из слоновой кости в шелком футляре.
Китайцы называли игру "ЧИ-ЧАО-ТЮ", что в переводе "Хитроумный узор из семи частей", а термин "Танграм" впервые был использован 1848 году Томасом Хиллом, в будущем президентом Гарвардского университета, в брошюре "Головоломки для обучения геометрии". Вероятно, что слово "танграм" произошло от слова "Тань” (что означает "китаец”) и корня "грамма” (в переводе с греческого "буква”). Упоминание танграма в литературе В книге Л.Кэрролла (Чарльз Лютвидж Доджсон) “Модная китайская головоломка” автор пишет, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, “упражняя свое терпение и находчивость”. Фотографии набора, которым пользовался Наполеон, содержатся в книге Джерри Слокума "The Tangram Book". Весь сюжет книги известного писателя и дипломата Роберт ван Гулик в романе “Убивающие ногтями” построен вокруг танграма. Правила игры 1. В каждую собранную фигуру должны входить все семь элементов.
2. При составлении фигур элементы не должны налегать друг на друга.
3. Элементы фигур должны примыкать один к другому. Примеры задач |
Игра «Морской бой»
Морской бой» — игра для двух участников, в которой игроки по очереди называют координаты на неизвестной им карте соперника. Если у соперника по этим координатам имеется корабль (координаты заняты), то корабль или его часть «топится», а попавший получает право сделать ещё один ход. Цель игрока — первым поразить все корабли противника.
Игра впервые была выпущена в виде настольной игры компаниейMilton Bradley Company в 1931-ом году.
Правила размещения кораблей (флота)[
Игровое поле — квадрат 10×10 каждого игрока, на котором размещается флот кораблей.
Горизонтали обычно нумеруются сверху вниз, а вертикали помечаются буквами слева направо. При этом используются буквы русского алфавита от «а» до «к» (буквы «ё» и «й» обычно пропускаются), либо буквы латинского алфавита от «a» до «l» (пропускается буква «j»). Иногда используется слово «республика» или «снегурочка», так как в этих 10-тибуквенных словах ни одна буква не повторяется. Поскольку существуют различные варианты задания системы координат, то об этом лучше заранее договориться.
Размещаются:
1 корабль — ряд из 4 клеток («линкоры», или «четырёхпалубные»)
2 корабля — ряд из 3 клеток («крейсеры», или «трёхпалубные»)
3 корабля — ряд из 2 клеток («эсминцы», или «двухпалубные»)
4 корабля — 1 клетка («подлодки», или «однопалубные»)
Другой вариант названия: -трубные (напр. двухтрубный).
При размещении корабли не могут касаться друг друга углами (встречаются, однако, варианты, когда это не запрещается).
Кроме того, встречаются варианты игры, когда корабли могут размещаться в виде квадрата ("четырехпалубные") или буквой "Г" ("трех-" и "четырехпалубные").
Рядом со «своим» квадратом чертится «чужой» такого же размера, только пустой. Это участок моря, где плавают чужие корабли противника.
При попадании в корабль противника — на чужом поле ставится крестик. Попавший стреляет ещё раз.
Поиск и потопление кораблей противника[
Перед началом боевых действий игроки бросают жребий или договариваются, кто будет ходить первым.
Игрок, выполняющий ход, совершает выстрел — называет вслух координаты клетки, в которой, по его мнению, находится корабль противника, например, «К1!» (верхняя правая клетка).
Если выстрел пришёлся в клетку, не занятую ни одним кораблём противника, то следует ответ «Мимо!» и стрелявший игрок ставит на чужом квадрате в этом месте точку. Право хода переходит к сопернику.
Если выстрел пришёлся в клетку, где находится многопалубный корабль (размером больше чем 1 клетка), то следует ответ «Ранил!» или «Попал!», кроме одного случая (см. пункт 3). Стрелявший игрок ставит на чужом поле в эту клетку крестик, а его противник ставит крестик на своём поле также в эту клетку. Стрелявший игрок получает право на ещё один выстрел.
Если выстрел пришёлся в клетку, где находится однотрубный корабль или последнюю непоражённую клетку многопалубного корабля, то следует ответ «Потоплен!» или «Убит!». Оба игрока отмечают потопленный корабль на листе. Стрелявший игрок получает право на ещё один выстрел.
Победителем считается тот, кто первым потопит все 10 кораблей противника. Проигравший имеет право попросить изучить после окончания игры у соперника игровое поле. Если проигравший находит какое-нибудь нарушение правил (см. ниже), то победа присуждается ему. Первоначальный победитель в свою очередь может попросить у соперника игровое поле для поиска нарушений. Если он их находит, то игроки сверяют чужие поля друг у друга. Если никаких несоответствий не замечено, то игра не засчитывается (оба проиграли). Тот, у кого чужое поле будет неверным (причём доказуемо неверным), будет проигравшим, а его соперник победителем. Игра также может закончиться раньше, чем когда будут потоплены все корабли, если нарушение правил будет замечено в течение игры. Проигравшим в этом случае будет считаться тот, у кого обнаружат нарушение правил, хотя он тоже может попросить игровое поле у соперника для поиска нарушений.
Тема : Задачи на складывание фигур - "Пентамино"
Цель
• Познакомить с логической игрой «пентамино»;
• развитие внимания, логического мышления.
Ход занятия
1. Организационный момент
Я очень рада вас видеть. Надеюсь, хорошее настроение будет сопутствовать Вам в течение всего урока.
2. Мотивационный материал
Сегодня на уроке мы с вами не будем решать задачи, а немножко поиграем. Поиграем в игру под названием «пентамино».
“Пентамино” - одна из самых популярных мировых головоломок, пик популярности пришелся на конец 60-х годов. В эту головоломку могут играть и дети и взрослые.
Пентамино — фигурка, составленная из пяти квадратиков (от слова "пента" - пять). Существует всего 12 пентамино.
Игра “Пентамино” состоит в том, чтобы из 12 этих деталей собирать разные картинки.
3. Составление фигур
При решении задач и головоломок фигурки можно вертеть и переворачивать.
Постройте фигурки.
Геометрия на спичках
Коробок спичек – отличное пособие для геометрических задач и развлечений, требующих сообразительности. Из спичек можно составить всевозможные прямолинейные фигуры, превращать одну фигуру, в другую путём перекладывания спичек, составлять слова. Даже теоремы можно доказывать на спичках! Причём спички – самое демократичное пособие, которое есть в любом доме. Никаких тебе дорогостоящих головоломок и электронных игр, а эффект тот же. (Конечно, если при этом не играть с огнём.) Поиски решения любой задачи развивают мышление, повышают уровень математической грамотности, учат мыслить нестандартно. Поэтому я предлагаю вашему вниманию урок геометрии на спичках в 7-м классе под названием «Осторожно, спички!».
Краткие советы по проведению
По ходу урока на доске учитель или ведущий поясняет ответы участников или даёт (демонстрирует) верные решения. Столы в классе расставлены так, чтобы все группы находились изолированно друг от друга. После прочтения вопроса учителем команды обсуждают решение в течении 3 мин. Первой отвечает та команда, которая раньше нашла верное решение. В начале урока учитель должен сделать введение на 3-5 мин, в котором можно напомнить участникам о необходимости умения логически мыслить, рассуждать в любой сфере человеческой деятельности. Далее поясняется ход урока и правила соревнования.
Вопросы командам:
1 Задача для разминки «Домик». Переложив 1 спичку, нужно повернуть домик в другую сторону.(Потребуется 11 спичек)






















 Ответ:
Ответ:
2 Арифметическая задача. Переложив 1 спичку, превратите равенство из неверного в верное. Задача имеет насколько решений.


























 Ответ:
Ответ:



3



 Задача на сообразительность. Как из пяти спичек, не ломая их сделать восемь?
Задача на сообразительность. Как из пяти спичек, не ломая их сделать восемь?
Ответ:
4 Задача с квадратами. (потребуется 16 спичек.)переложив с одного места на другое 2 спички, сделайте из 5 квадратов 4 квадрата таких же размеров.












 Ответ:
Ответ:



















5





 Задача «Золотая рыбка». (потребуется 8 спичек). Передвинув 3 спички, заставьте рыбку плыть в другую сторону.
Задача «Золотая рыбка». (потребуется 8 спичек). Передвинув 3 спички, заставьте рыбку плыть в другую сторону.
 Ответ:
Ответ:








6





 Задача о чистоте и порядке. (потребуется 5 спичек). Переложив 2 спички, уберите мусор из совка. При этом спичку, изображающую мусор, не трогать. «Пустой» совок не обязательно должен стоять на ножке, он может лежать на боку, быть повёрнутым, но не должен терять своей формы.
Задача о чистоте и порядке. (потребуется 5 спичек). Переложив 2 спички, уберите мусор из совка. При этом спичку, изображающую мусор, не трогать. «Пустой» совок не обязательно должен стоять на ножке, он может лежать на боку, быть повёрнутым, но не должен терять своей формы.



 Ответ:
Ответ:
7 Задача – шутка. Из тринадцати спичек, длиной в 4 см каждая, нужно сложить метр.
О













 твет:
твет:
8















 Шпионская задача «Осада крепости» из 16-ти спичек выложен «план крепости», окруженной глубоким рвом. Как при помощи двух досок – спичек, длина которых равняется ширине рва, пробраться в крепость?
Шпионская задача «Осада крепости» из 16-ти спичек выложен «план крепости», окруженной глубоким рвом. Как при помощи двух досок – спичек, длина которых равняется ширине рва, пробраться в крепость?

















 Ответ:
Ответ:
9






 Арифметическая задача. (Потребуется 12 спичек). Сначала в 1) убрать, а затем в 2) переложить оду спичку, получить верное равенство.
Арифметическая задача. (Потребуется 12 спичек). Сначала в 1) убрать, а затем в 2) переложить оду спичку, получить верное равенство.
Ответы:
1














 ) 2)
) 2)
10 Абстрактная задача. Из шести спичек построить четыре равносторонних треугольника.
О
 твет: задача в пространстве: тетраэдр.
твет: задача в пространстве: тетраэдр.





Подведение итогов
Рисуем по координатам
Я буду диктовать координаты, а вы на заготовленных координатных плоскостях отмечаете точки и последовательно соединяете их с предыдущей точкой с помощью отрезков. Единичный отрезок равен одной клеточке.
Динозавр
(1;2) (3;4) (7;5) (9;4) (14;0) (20;-6) (10;0) (9;-2) (9;-4) (6;-4) (7;-3) (7;-2) (2;-2)
(2;-4) (-1;-4) (0;-3) (0;0) (-5;4) (-7;4) (-8;5) (-6;7) (-5;7) (1;2) глаз (-6;6).
- Да, мы с вами и не предполагали, что на земле остались места, в которых еще живут динозавры. Мы не должны никому говорить об этом, иначе уже завтра сюда приедут браконьеры и будут на них охотиться.
Физминутка /слайд 9/
На болоте две подружки
Две зеленые лягушки
Рано утром умывались,
Полотенцем растирались.
Ножками топали,
Ручками хлопали.
Вправо, влево наклонялись
И обратно возвращались.
V. Пещера.
- В этом заповеднике есть интересная пещера, в которой можно найти наскальные рисунки, но рисунки очень странные. Каждый рисунок завершен только наполовину. К нам в руки попали только копии одного из рисунков и мы с вами попробуем его дорисовать. /слайд 10/
/Детям раздаются карточки для работы с симметрией/
- На что похожа эта часть рисунка? (Кувшин)
- Для того чтобы завершить рисунок, вы должны поочередно предлагать координаты продолжения рисунка. Координаты должны быть последовательными, чтобы с помощью отрезков можно было завершить рисунок.
/(7;10) (4;8) (3;6) (3;4) (6;0) (7;-3) (7;-6) (5;-8) (3;-9) (6;10)/
VI. Самостоятельная работа.
- Мы заканчиваем свое исследование затерянного мира, но в конце нашего путешествия нам прислали спецзадание: попытаться найти давно забытые растения. Задание пришло закодированным, и что нам с вами нужно искать, мы узнаем, если расшифруем послание при помощи координат.
- У вас у каждого на столе лежит карточка с заданными координатами вы должны будете в своей тетради построить координатную плоскость, единичный отрезок равный 1см, отметить точки и последовательно соединив их, вы получите рисунок, а какой мы узнаем после того как вы выполните задание.
- Но прежде чем приступить к работе, давайте еще раз вспомним построение точки по ее координатам. Если вы даже не умеете рисовать, то с помощью последовательных соединений точек можно нарисовать любой рисунок.
Отметить на координатной плоскости точки, последовательно соединив их отрезками:
(-2;2) (-3;-1) (-6;-2) (-5;1) (1;3) (4;-6) (3;-2) (2;-1) (-1;-1) (-4;2) (-6;3) (-3;3) (2;6) (-1;5) (-2;2) (-5;3) (-6;6) (-3;5)
(-5;6) (-2;4) (-2;7) (-1;5) (2;2) (2;-1) (-1;2).
(-1;-1) (2;-2) (1;1)
(-2;2) (-2;-2) (-5;-6).
Элементы статистики
Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, про исходящих в природе и обществе.
Среднее арифметическое ряда чисел – это частное от деления суммы этих чисел на число слагаемых.
Среднее арифметическое ряда чисел - результат после деления суммы чисел на их количество
Пример1. Выделили группу из семиклассников и попросили отметить в определнный день время (мин), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: 23, 18, 25, 20, 25,25, 32, 37, 34 , 26, 34, 25.
4
Найдем сколько минут в среднем учащиеся затратили на выполнение домашнего задания по алгебре ( 23 + 18 + 25 + 20 + 25 + 25 + 32 + 37 + 34 + 26 + 34 + 25 ): 12 = =324 : 12 = 27 мин.
27 – среднее арифметическое рассматриваемого ряда
Где применяют среднее арифметическое: В сельском хозяйстве на фермах, если все количество молока (в литрах) , полученное за сутки делят на количество коров , то узнают среднесуточный удой от одной коровы. Среднюю урожайность пшеницы с 1га находят так: весь полученный урожай пшеницы (в центнерах) делят на площадь полей, засеянных этой культурой (в га). Средняя выработка рабочего бригады за смену = ( работа всей бригады) : (количество рабочих)
Но иногда вычисление среднего арифметического не дает полезной информации. Например: Нецелесообразно использовать такие данные как: средняя температура больных в терапевтическом отделении, средний размер обуви, который носят учащиеся школы, средняя урожайность зерновых и бахчевых культур в фермерском хозяйстве
Далее ввожу очень важное понятие
^ Упорядоченный ряд чисел – такой ряд, в котором каждое последующее число не меньше (или не больше) предыдущего ( другими словами расположить числа в порядке возрастания )
Если ряд упорядочен, то легко находить следующие характеристики: размах и моду
Опр. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Пример2 В течение суток отмечали каждый час температуру воздуха в ст Старовеличковской в ноябре 2010 года
7, 7, 6, 6, 5. 5, 6, 7, 9, 11, 13, 16, 18, 20, 22, 21, 18, 15, 13, 10, 9, 9, 8, 8.
Найдите среднее арифметическое и размах этого ряда
Решение .
1) Упорядочим данный ряд, получим
5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9, 10, 11, 13, 13, 15, 16, 18, 20, 21, 22, 22.
2). Найдем среднее арифметическое
(2 ∙ 5 + 6 ∙3 + 7 ∙ 3 +8 ∙2 + 9 ∙ 3 + 10 +11+ 13 ∙ 2 + 15 + 18 + 20 + 12 + 22 ∙ 2) : 24 =
=248 : 24 = 10,3
3) Размах ряда чисел равен 22 – 5 = 17
Среднее арифметическое показывает какова среднесуточная температура воздуха, а размах характеризует колебание температуры в течение этих суток.
Опр. Модой ряда называется число, наиболее часто встречающееся в данном ряду.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Пример3. Найти моду и размах следующих числовых рядов:
5
а) 12, 14, 13, 15, 16, 17, 19.
б) 47, 46, 50, 52, 47, 52, 49, 45.
в) 69, 68, 66, 70, 74, 63, 74, 72.
Решение
Каждый из этих рядов сначала упорядочим, а затем найдем моду и размах
а) 12, 13, 14, 15, 16, 17, 19.
моды у этого ряда нет, размах равен 19 – 12= 7
стр. 3
б) 45, 46, 47, 47, 49, 50, 52, 52.
у этого ряда две моды : 47 и 52.
52 – 45 = 7 – размах ряда
в) 63, 66, 68, 69, 70, 72, 74, 74.
число 74 – мода ряда,
74 – 63 = 11 размах ряда
Примеры 1-3 разбираем вместе с учащимся, они помогают упорядочить ряд, найти среднее арифметическое , моду и размах . Все примеры записываются в тетрадь.
В оставшееся на уроке время решаем подобные задания, с целью закрепления полученных знаний
Теперь уже кто- то из уч-ся решает предложенные упражнения у доски, а остальные в тетрадях. Решаем с комментариями, ссылаясь на определения новых понятий
№ 168 . Найдите среднее арифметическое, размах и моду ряда чисел:
а) 32, 26, 18, 26, 15, 21, 26; б) 21,18,5,25,3,18,5,17,9;
в) 67,1, 68,2, 67,1, 70,4, 68,2; г) 0,6, 0,8, 0,5, 0,9, 1,1.
Самостоятельная работа
ВАРИАНТ1
1. В аттестате о среднем образовании у выпускника школы - оказались следующие оценки: 4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4;
С каким средним баллом окончил школу этот выпускник? Укажите наиболее типичную для него оценку в аттестате. Какие статистические характеристики вы использовали при ответе?
2. Найти среднее арифметическое, размах, моду ряда чисел 321, 323, 321, 324, 319.
ВАРИАНТ2
1. В аттестате о среднем образовании у выпускника школы - оказались следующие оценки :3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4;
С каким средним баллом окончил школу этот выпускник? Укажите наиболее типичную для него оценку в аттестате. Какие статистические характеристики вы использовали при ответе?
2. Найти среднее арифметическое, размах, моду ряда чисел 253, 257, 254, 255, 254.
Ответы Вариант №1
Задание1
Упорядочим ряд 4,4, 4, 4 ,4, 4,4, 4, 4, 5, 5, 5, 5, 5, 5.
( 4∙9 + 5∙ 6 ) : 15 = 66: 15 = 4,4 – средний балл аттестата
4- типичная оценка
При ответе использовали : среднее арифметическое и моду ряда
Задание2
Упорядочим ряд 319, 321, 321,323, 324.
( 319 + 321 + 321 + 323 + 324 ) : 5 = 321,4 – среднее арифметическое
321 – мода ряда
324 – 319 = 5 – размах ряда
Вариант №2
7
Упорядочим ряд 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5
( 3 ∙ 9 + 4 ∙5 + 5 ) : 15 = ( 27 + 25 ) : 15 = 52 : 15 = 3,46
3 – типичная оценка
При ответе использовали : среднее арифметическое и моду ряда
Задание2
Упорядочим ряд 253, 254, 254, 255, 257.
( 253 + 254 + 254 + 255 +257 ) : 5 = 254,6 - среднее арифметическое
254 – мода ряда
257 – 253 = 4 - размах ряда
Медиана как статистическая характеристика»
Опр. Медианой упорядоченного ряда чисел с нечетным числомчленов называется число, записанное посередине
Опр. Медианой упорядоченного ряда с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Опр. Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Пример 1. В таблице показан расход электроэнергии в январе жильцами 9 квартир:
|
Номер квартиры
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Расход электроэнергии, кВт ∙ ч
|
85
|
64
|
78
|
93
|
72
|
91
|
72
|
75
|
82
|
Найдите медиану указанного ряда чисел.
Решение. Составим из данных, приведенных в таблице, упорядоченный ряд:
8
64, 72, 72, 78,82, 85, 91,93.
В полученном упорядоченном ряду девять чисел – нечетное число членов. Посередине находится пятый член ряда – это 78. Значит, медиана данного ряда равна 78.
Ответ: 78.
Пример 2. В таблице показан расход электроэнергии в январе жильцами 10 квартир:
|
Номер квартиры
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Расход электроэнергии, кВт ∙ ч
|
85
|
64
|
78
|
93
|
72
|
91
|
72
|
75
|
82
|
88
|
Найдите медиану указанного ряда чисел.
Решение. Составим из данных, приведенных в таблице, упорядоченный ряд:
64, 72, 72, 78,82, 85, 88, 91,93.
В этом числовом ряду четное число членов и имеются два числа, расположенные в середине ряда: 78 и 82. Найдем среднее арифметическое этих чисел: . Число 80, не являясь членом ряда, разбивает этот ряд на две одинаковые по численности
группы, поэтому говорят, что число 80 медиана данного упорядоченного ряда, а также исходного ряда данных, записанных в таблице.
Ответ: 80.
186. Найдите медиану ряда чисел:
а) 30, 32, 37, 40, 41, 52, 45, 49, 52; б) 102, 104, 205, 207, 327, 408, 417;
187. Найдите среднее арифметическое и медиану ряда чисел:
а) 27, 29, 23, 31, 21, 34;
1. В таблице показано число посетителей выставки в разные дни недели:
|
День недели
|
Пн
|
Вт
|
Ср
|
Чт
|
Пт
|
Сб
|
Вс
|
|
Число посетителей
|
604
|
638
|
615
|
636
|
625
|
710
|
724
|
Найдите медиану указанного ряда данных. В какие дни недели число посетителей выставки было больше медианы?
2. Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
Чтобы активизировать работу учащихся можно организовать работу у доски таким образом: первый уч-ся упорядочивает ряд чисел, второй находит среднее арифметическое, третий находит медиану, четвертый отвечает на вопрос , поставленный в задаче
3. Найдите медиану, размах, моду ряда 2,4; 2,1; 2,7; 2,4; 2,5; 2,3
8

 Получите свидетельство
Получите свидетельство Вход
Вход














 ). Решите задачу с девятью мостами, аналогичную предыдущей по условию и требованию (рис 5).
). Решите задачу с девятью мостами, аналогичную предыдущей по условию и требованию (рис 5).















 Рабочая программа кружка «Математика может быть интересной» (5-й класс) (1.19 MB)
Рабочая программа кружка «Математика может быть интересной» (5-й класс) (1.19 MB)
 0
0 7691
7691 1588
1588 Нравится
1
Нравится
1


