методическим советом. Директор МОАУ Гимназия №1
Протокол от__ ________ №____ _____________ Н.В. Николаева
управляющим советом.
- расширить сведения о свойствах функций, ознакомить учащихся со свойствами и графиком степенной функции, выработать умение строить график степенной функции и применять графические представления для решения неравенств с одной переменной; выполнять преобразования;
- выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными, и решать текстовые задачи с помощью составления таких систем;
- дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида;
Для разработки рабочей программы мною выбрана примерная программа среднего полного образования по математике. Выбор определяется тем, что примерная программа составлена Министерством образования РФ в соответствии с требованиями федерального компонента государственного стандарта среднего полного образования и обязательного минимума содержания основных образовательных программ по математике в средней школе.
Были внесены изменения в количество часов по основным темам, разделам. При этом минимум часов, определяемый примерной программой не нарушается.
Согласно федеральному базисному учебному плану на изучение математики в 9 классе отводится 170 часов из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии может быть следующим:
3 часа в неделю алгебры и 2 часа в неделю геометрии в течение всего учебного года, итого 102 часов алгебры и 68 часов геометрии.
Плановых контрольных уроков - 12.
Проблемно – поисковая, исследовательская, здоровье сберегающая, развивающее обучение.
Линейные и квадратные неравенства (повторение).
Рациональное неравенство. Метод интервалов. Множества и операции над ними.
Система неравенств. Решение системы неравенств.
Рациональное уравнение с двумя переменными. Решение уравнения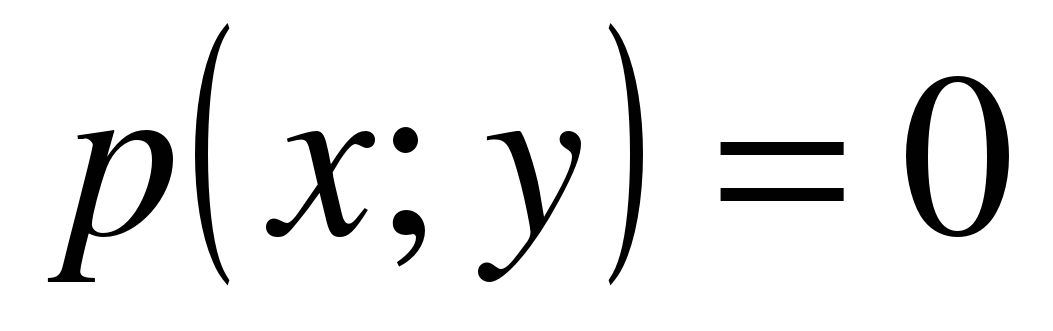 
. Равносильные
уравнения с двумя переменными. Формула расстояния между двумя точками координатной
плоскости. График уравнения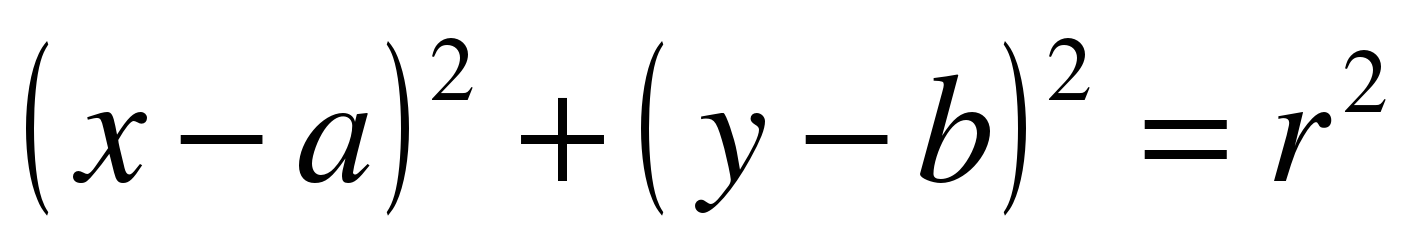 
. Система уравнений с двумя переменными.
Решение системы уравнений. Неравенства и системы неравенств с двумя переменными.
Методы решения систем уравнений (метод подстановки, алгебраического сложения, введения
новых переменных) равносильность систем уравнений.
Системы уравнений как математические модели реальных ситуаций.
Функция. Независимая переменная. Зависимая переменная. Область определения функции.
Естественная область определения функции. Область значений функции.
Способы задания функции (аналитический, графический, табличный, словесный).
Свойства функций (монотонность, ограниченность, выпуклость, наибольшее и наименьшее
значения, непрерывность). Исследование функций: 
, 
, 
, 
, 
,
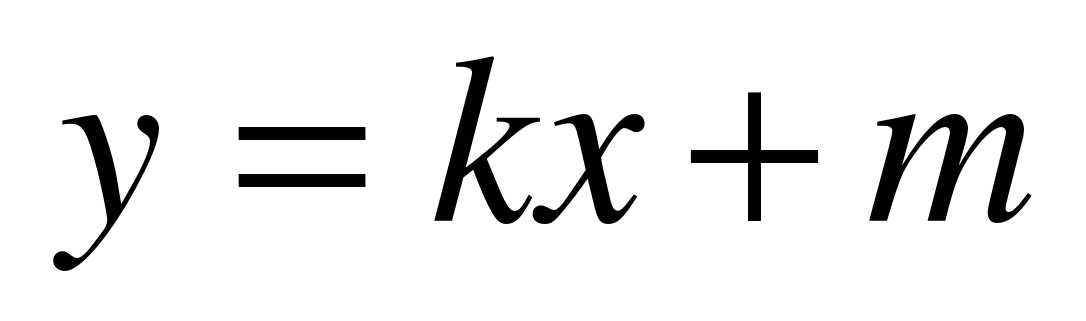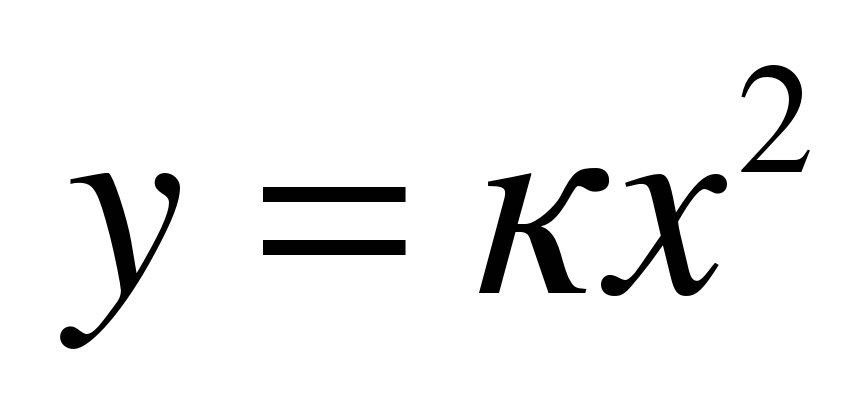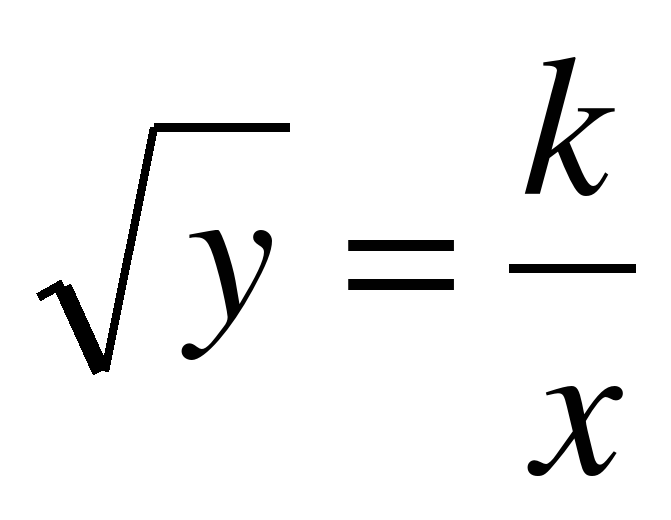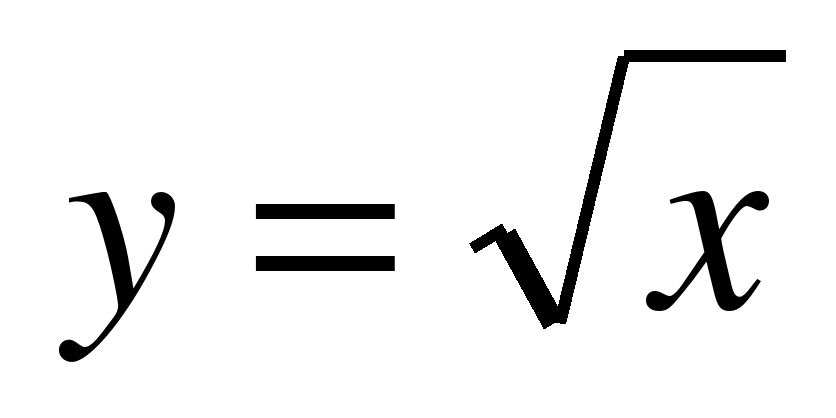Чётные и нечётные функции. Алгоритм исследования функции на чётность. Графики чётной и
нечётной функций.
Степенная функция с натуральным показателем, её свойства и график. Степенная функция с
отрицательным целым показателем, её свойства и график. Функция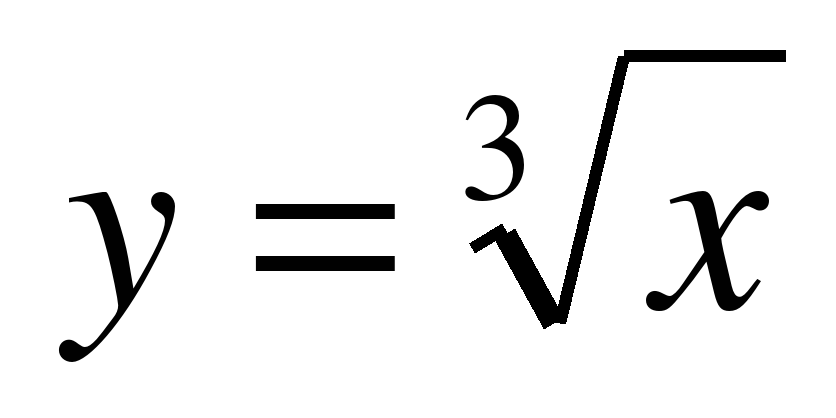 
, её свойства и
график.
Числовая последовательность. Способы задания числовых последовательностей (аналитический,
словесный, рекуррентный). Свойства числовых последовательностей. Арифметическая
прогрессия. Формула n-го члена. Формула суммы членов конечной арифметической прогрессии.
Характеристическое свойство. Геометрическая прогрессия. Формула n-го члена. Формула суммы
членов конечной геометрической прогрессии. Характеристическое свойство. Прогрессии и
банковские расчёты.
Комбинаторные задачи. Правило умножения. Факториал. Перестановки.
Группировка информации. Общий ряд данных. Кратность варианты измерения. Табличное
представление информации. Частота варианты. Графическое представление информации.
Полигон распределения данных. Гистограмма. Числовые характеристики данных измерения
Вероятность. Событие (случайное, достоверное, невозможное). Классическая вероятностная
схема. Противоположные события. Несовместные события. Вероятность суммы двух событий.
Вероятность противоположного события. Статистическая устойчивость. Статистическая
вероятность.
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число.
Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в
координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
понятие вектора, правила сложения, вычитания векторов, правило умножения вектора на число, правило разложения вектора по двум неколлинеарным векторам, уравнение прямой, уравнение окружности.
Строить векторы, складывать и вычитать векторы, строить равные веторы находить координаты вектора, решать простейшие задачи в координатах, составлять уравнение окружности и уравнение прямой , уравнение окружности и уравнение прямой
Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное
произведение векторов и его применение в геометрических задачах.
Понятия синуса, косинуса и тангенса угла, формулу для вычисления координаты точки, теорему синуспов, теорему косинусов, понятие скалярного произведения векторов.
Решать задачи, применяя формулы для вычисления координаты точки, теоремы синусов и косинусов, находить скалярное произведение векторов.
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
многоугольника и описанного около него, формулы для вычисления площади правильного многоугольника, формулы длины окружности и дуги окружности, формулы площади круга и кругового сектора.
Строить правильные многоугольники вписанные в окружность и описанные около неё, решать задачи, применяя формулы для вычисления площади правильного многоугольника, формулы длины окружности и дуги окружности, формулы площади круга и кругового сектора.
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.
Понятие движения, виды движения: параллельный перенос, поворот.
Строить фигуры, полученные из данных параллельным переносом и поворотом вокруг точки.
Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.
1. Мордкович, А. Г. Алгебра. 9 класс : в 2 ч. Ч. 1 : учеб. для учащихся общеобразоват. учреждений / А. Г. Мордкович. – М. : Мнемозина, 2010.
2. Мордкович, А. Г. Алгебра. 9 класс : в 2 ч. Ч. 2 : задачник для учащихся общеобразоват. учреждений / А. Г. Мордкович [и др.] ; под ред. А. Г. Мордковича. – М. : Мнемозина, 2010.
3. Мордкович, А. Г. Алгебра. 9 класс : метод. пособие для учителя / А. Г. Мордкович. – М. : Мнемозина, 2010.
4. Мордкович, А. Г. Алгебра. 7–9 классы : тесты / А. Г. Мордкович, Е. Е. Тульчинская. – М. : Мнемозина, 2011.
5. Александрова, Л. А. Алгебра. 8 класс : контрольные работы / Л. А. Александрова ; под ред. А. Г. Мордковича. – М. : Мнемозина, 2010.
6. Александрова, Л. А. Алгебра. 9 класс : самостоятельные работы / Л. А. Александрова ; под ред. А. Г. Мордковича. – М. : Мнемозина, 2010.
7. Геометрия: учебник для 7—9 кл. / [Л. С. Атанасян, В. Ф. Бутузов, С. В. Кадомцев и др.]. — М.: Просвещение, 2009 г.
8. Изучение геометрии в 7, 8, 9 классах: метод, рекомендации: кн. для учителя / [Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др.]. - М.: Просвещение, 2003 — 2008.
9. Зив Б.Г. Геометрия: Дидакт. материалы для 9 кл. / Б.Г. Зив, В.М. Мейлер. — М.: Просвещение, 2004—2008.
10. Гаврилова Н.Ф. Поурочные разработки по геометрии. 9 класс. М.: ВАКО, 2004 – (В помощь школьному учителю)
11. Рабочая тетрадь по геометрии для 9 класса общеобразовательных учреждений М: «Просвещение» 2008 г Авторы: Л. С. Атанасян, В. Ф. Бутузов;
12. А.В. Фарков / Контрольные работы, тесты, диктанты по геометрии к учебнику Л. С. Атанасяна, В. Ф. Бутузова
1. Арутюнян, Е. Б. Математические диктанты для 5–9 классов / Е. Б. Арутюнян. – М. : Просвещение, 2007.
2. Кострикина, Н. П. Задачи повышенной трудности в курсе алгебры 7–9 классов / Н. П. Кострикина. – М. : Просвещение, 2007.
3. Дудницын, Ю. Алгебра. Карточки с заданиями для 9 класса / Ю. Дудницын, В. Кронгауз. – М. : Просвещение, 2007.
1. Мантуленко, В. Г. Математика : кроссворды для школьников / В. Г. Мантуленко, О. Г. Гетманенко. – Ярославль : Академия развития, 2004.
2. Пичурин, Л. Ф. За страницами учебника алгебры : книга для учащихся 7–9 классов средней школы / Л. Ф. Пичурин. – М. : Просвещение, 1990.
3. Черкасов, О. Ю. Математика : справочник для старшеклассников и поступающих в вузы / О. Ю. Черкасов, А. Г. Якушев. – М. : АСТ-Пресс Школа, 2006.
4. Энциклопедия для детей. Т. 11. Математика / под ред. М. Аксеновой. – М. : Аванта+, 2007.
5. Я познаю мир. Великие ученые : энциклопедия.– М. : АСТ : Астрель : Ермак, 2004.
6. Я познаю мир. Математика : энциклопедия.– М. : АСТ : Астрель : Хранитель : Харвест, 2007.
1. Министерство образования РФ. – Режим доступа : http://www.informika.ru; http://www.ed.gov.ru; http://www.edu.ru
2. Тестирование online: 5–11 классы. – Режим доступа : http://www.kokch.kts.ru/cdo
3. Педагогическая мастерская, уроки в Интернет и многое другое. – Режим доступа : http:// teacher.fio.ru
4. Новые технологии в образовании. – Режим доступа : http://edu.secna.ru/main
5. Путеводитель «В мире науки» для школьников. – Режим доступа : http://www.uic.ssu. samara.ru/~nauka
6. Мегаэнциклопедия Кирилла и Мефодия. – Режим доступа : http://mega.km.ru
7. Сайты энциклопедий, например: http://www.rubricon.ru; http. – Режим доступа ://www. encyclopedia.ru
8. Единая коллекция цифровых образовательных ресурсов по математике. – Режим доступа : http://school-collection.edu.ru/collection
методическим советом. Директор МОАУ Гимназия №1
Протокол от__ ________ №____ _____________ Н.В. Николаева
управляющим советом.
| № | Дата | Тема урока | Кол-во часов | Тип (вид) урока | Основные ЗУН соответствующие ГСО |
| план | факт |
|
|
| Вводное повторение по курсу алгебры
| 6 |
|
|
|
|
| Вводное повторение геометрии
| 2 |
|
-
|
|
| Инструктаж по ТБ при проведении уроков в кабинете математики. Алгебраические дроби | 1 | Тип: комбинированный Вид: смешанный | Уметь выполнять все действия с алгебраическими дробями, сокращать дроби. |
-
|
|
| Квадратичная функция. Функция 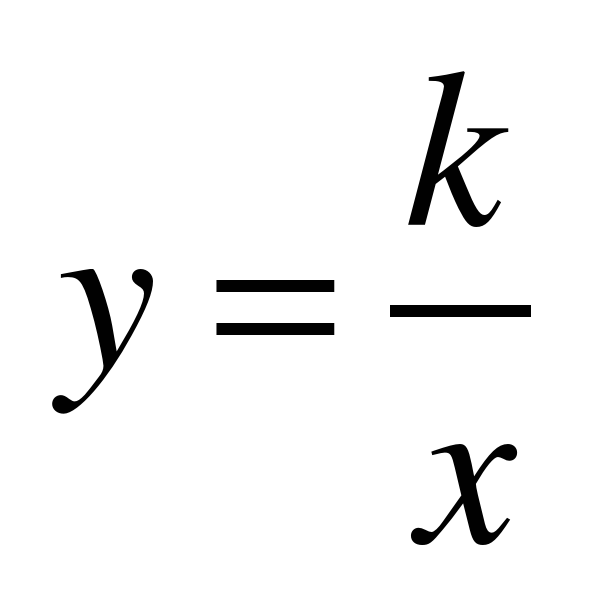 . Функция 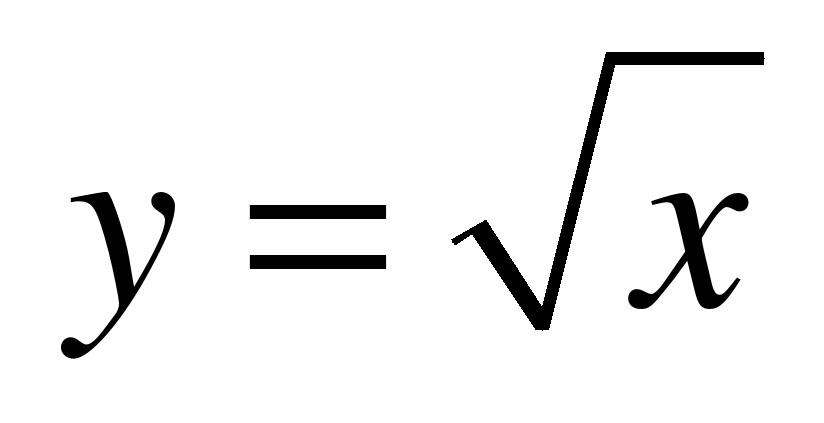 . Свойства квадратного корня | 1 | Тип: комбинированный Вид: смешанный | Знать свойства функци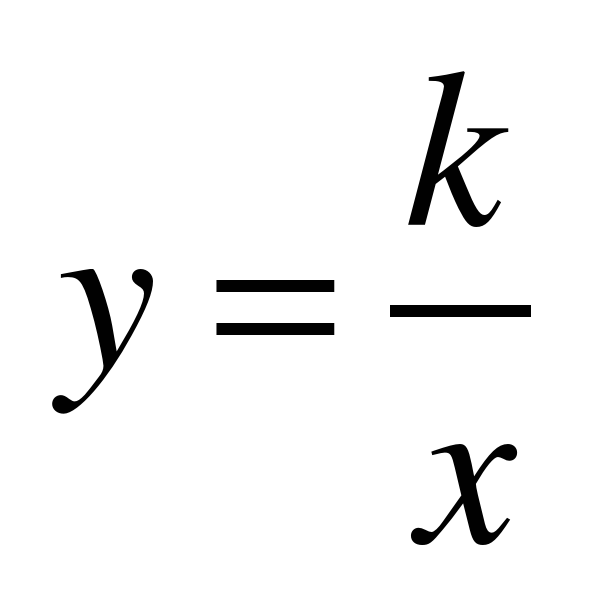й и 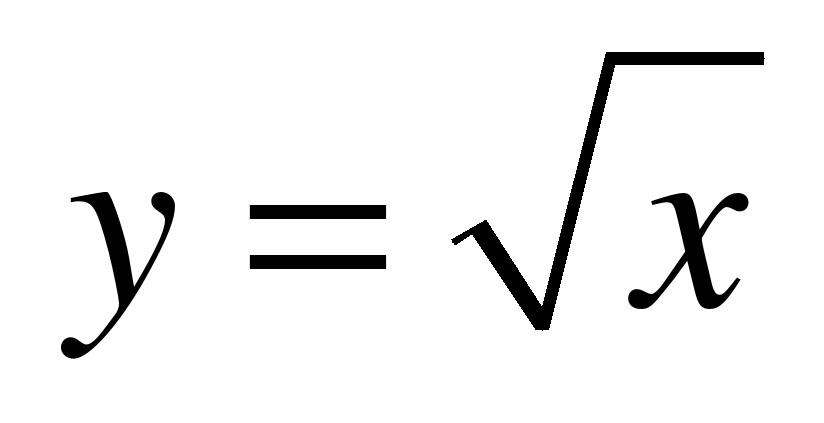. Уметь: – строить графики функций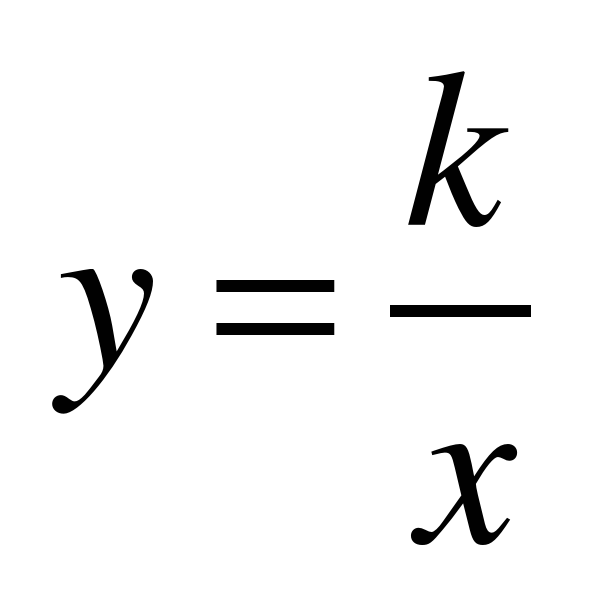
и 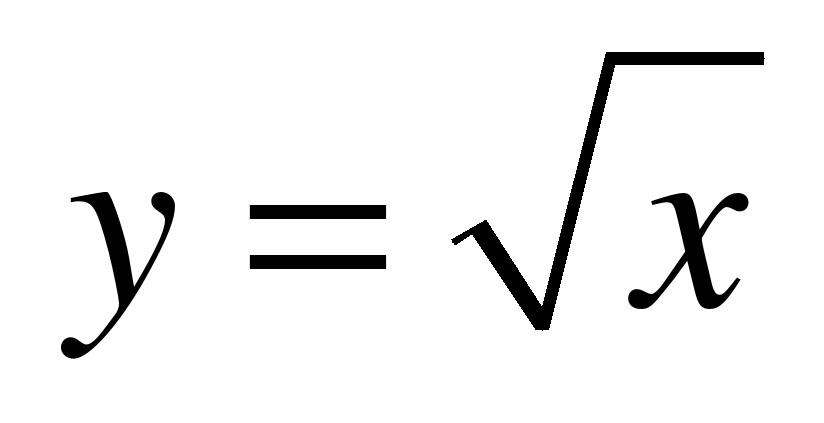; – адекватно воспринимать устную речь, проводить информационно-смысловой анализ текста, приводить примеры |
-
|
|
| Действительные числа. Квадратные уравнения | 1 | Тип: комбинированный Вид: смешанный | Знать понятие действительного числа. Уметь: – использовать формулы корней квадратного уравнения, преобразовывать формулы; – заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц |
-
|
|
| Теорема Пифагора. Свойства медиан, биссектрис и высот треугольника. | 1 | Тип: комбинированный Вид: практикум | Знать и понимать: понятия: медиана, биссектриса, высота, треугольника, параллелограмм, трапеция, ромб, квадрат. Уметь: выполнять задачи из разделов курса VIII класса, используя теорию: теорема Пифагора, свойство средней линии треугольника, формулы вычисления площади треугольника; свойства, признаки параллелограмма, ромба, прямоугольника. |
-
|
|
| Четырехугольники. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Неравенства и их свойства | 1 | Тип: комбинированный Вид: практикум | Уметь: – решать простейшие линейные и квадратные неравенства с одной переменной; – отмечать на числовой прямой решение неравенства; – аргументированно отвечать на поставленные вопросы, осмыслить ошибки и устранить их. |
-
|
|
| Неравенства и их свойства | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Вводный контроль | 1 | Тип: обобщение и систематизация знаний Вид: контрольная работа | Уметь: – владеть навыками самоанализа
и самоконтроля; – обобщать и систематизировать знания по основным темам курса алгебры 8 класса; – предвидеть возможные последствия своих действий |
|
|
|
| Векторы. | 8 |
|
-
|
|
| Понятие вектора. Откладывание вектора от данной точки. | 1 | Тип: изучение нового материала Вид: беседа | Уметь изображать и обозначать векторы; определять сонаправленные и противоположно-направленные вектора, сравнивать вектора. Уметь откладывать от любой точки плоскости вектор, равный данному. |
-
|
|
| Сумма двух векторов. Сумма нескольких векторов. | 1 | Тип: изучение нового материала Вид: смешанный | Знать законы сложения векторов, уметь строить сумму двух и более векторов, пользоваться правилом треугольника, параллелограмма, многоугольника |
|
|
|
| Рациональные неравенства и их системы.
| 14 |
|
-
|
|
| Линейные и квадратные неравенства | 1 | Тип: изучение нового материала Вид: смешанный | Иметь представление о решении линейных и квадратных неравенств с одной переменной. Знать, как проводить исследование функции на монотонность. Уметь: – решать линейные и квадратные неравенства с одной переменной, содержащие модуль; – решать неравенства, используя графики; – составлять текст научного стиля |
-
|
|
| Линейные и квадратные неравенства. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Рациональные неравенства. | 1 | Тип: изучение нового материала Вид: смешанный | Иметь представление о решении рациональных неравенств методом интервалов. Знать и применять правила равносильного преобразования неравенств. Уметь решать дробно-рациональные неравенства методом интервалов, передавать информацию сжато, полно, выборочно. |
-
|
|
| Вычитание векторов. | 1 | Тип: комбинированный Вид: практикум | Знать правило построения разности векторов, уметь строить разность векторов |
-
|
|
| Решение задач по теме «Сложение и вычитание векторов». | 1 | Тип: комбинированный Вид: самостоятельная работа | Знать законы сложения и вычитания векторов, уметь строить сумму и разность двух и более векторов, пользоваться правилом треугольника, параллелограмма, многоугольника |
-
|
|
| Рациональные неравенства. | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о решении рациональных неравенств методом интервалов. Знать и применять правила равносильного преобразования неравенств. Уметь решать дробно-рациональные неравенства методом интервалов, передавать информацию сжато, полно, выборочно. |
-
|
|
| Рациональные неравенства. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Рациональные неравенства. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Умножение вектора на число. | 1 | Тип: изучение нового материала Вид: смешанный | Знать свойства умножения вектора на число, уметь решать задачи на умножение вектора на число |
-
|
|
| Применение векторов к решению задач. | 1 | Тип: комбинированный Вид: практикум | Уметь решать задачи на применение законов сложения, вычитания векторов, умножения вектора на число |
-
|
|
| Множества и операции над ними
| 1 | Тип: изучение нового материала Вид: смешанный | Уметь - приводить примеры конечных и бесконечных множеств; - находить объединение и пересечение конкретных множеств, разность множеств; - приводить примеры несложных классификаций; - иллюстрировать теоретико- множественные понятия с помощью кругов Эйлера. |
-
|
|
| Множества и операции над ними | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Множества и операции над ними | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Средняя линия трапеции. Решение задач по теме «Векторы». | 1 | Тип: изучение нового материала Вид: смешанный | Знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции. Уметь решать задачи на применение векторов |
-
|
|
| Контрольная работа по теме «Векторы». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь самостоятельно применять полученные теоретические знания на практике |
-
|
|
| Системы рациональных неравенств.
| 1 | Тип: изучение нового материала Вид: смешанный | Иметь представление о решении систем рациональных неравенств. Знать о способах решения систем рациональных неравенств. Уметь: – решать системы квадратных неравенств, используя графический метод; – решать двойные неравенства; – решать системы простых рациональных неравенств методом интервалов; – объяснить изученные положения на самостоятельно подобранных конкретных примерах; – извлекать необходимую информацию из учебно-научных текстов. |
-
|
|
| Системы рациональных неравенств. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Системы рациональных неравенств. | 1 | Тип: комбинированный Вид: практикум |
|
|
|
| Метод координат.
| 10 |
|
-
|
|
| Разложение вектора по двум неколлинеарным векторам. | 1 | Тип: изучение нового материала Вид: смешанный | Уметь применять теорему о разложении вектора по двум неколлинеарным векторам, знать правила действий над векторами с заданными координатами.. |
-
|
|
| Координаты вектора. | 1 | Тип: изучение нового материала Вид: смешанный | Раскладывать вектор по двум неколлинеарным векторам, находить координаты вектора, выполнять действия над векторами, заданными координатами |
-
|
|
| Решение рациональных неравенств и их систем. | 1 | Тип: повторительно-обобщающий Вид: самостоятельная работа | Уметь: – решать рациональные неравенства и системы рациональных неравенств; |
-
|
|
| Контрольная работа по теме «Рациональные неравенства и их системы». | 1 | Тип: контроль знаний и умений Вид: контрольная работа
| Уметь: – решать рациональные неравенства и системы рациональных неравенств; – владеть навыками самоанализа и самоконтроля Дифференцированные контрольно-измерительные материалы |
|
|
|
| Системы уравнений
| 18 |
|
-
|
|
| Основные понятия. | 1 | Тип: изучение нового материала Вид: лекция | Иметь понятие
о решении системы уравнений и неравенств. Знать равносильные преобразования уравнений и неравенств с двумя переменными. Уметь определять понятия, приводить доказательства |
-
|
|
| Простейшие задачи в координатах. | 1 | Тип: комбинированный Вид: смешанный | Уметь выводить формулы координат вектора через координаты его конца и начала координат середины отрезка, длины вектора и расстояния между двумя точками. |
-
|
|
| Простейшие задачи в координатах. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Основные понятия. | 1 | Тип: комбинированный Вид: практикум | Иметь понятие о решении системы уравнений и неравенств. Знать равносильные преобразования уравнений и неравенств с двумя переменными. Уметь определять понятия, приводить доказательства |
-
|
|
| Основные понятия. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Основные понятия. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Решение задач методом координат. | 1 | Тип: комбинированный Вид: смешанный | Решать задачи с помощью формул координат вектора через координаты его начала и конца, координат середины отрезка, длины вектора и расстояния между двумя точками. |
-
|
|
| Уравнения окружности. | 1 | Тип: изучение нового материала Вид: беседа | Записывать уравнения прямых и окружностей, использовать уравнения при решении задач, строить окружности и прямые, заданные уравнениями. |
-
|
|
| Основные понятия. | 1 | Тип: комбинированный Вид: консультация | Иметь понятие
о решении системы уравнений и неравенств. Знать равносильные преобразования уравнений и неравенств с двумя переменными. Уметь определять понятия, приводить доказательства |
-
|
|
| Методы решения систем уравнений. | 1 | Тип: изучение нового материала Вид: беседа | Знать алгоритм метода подстановки. Уметь использовать графики при решении системы уравнений, использовать для решения познавательных задач справочную литературу. Уметь: – при решении систем уравнений применять метод алгебраического сложения и метод введения новой переменной; – объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
-
|
|
| Методы решения систем уравнений. | 1 | Тип: комбинированный Вид: практикум | Знать алгоритм метода подстановки. Уметь использовать графики при решении системы уравнений, использовать для решения познавательных задач справочную литературу. Уметь: – при решении систем уравнений применять метод алгебраического сложения и метод введения новой переменной; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Уравнение прямой. | 1 | Тип: изучение нового материала Вид: беседа | Записывать уравнения прямых и окружностей, использовать уравнения при решении задач, строить окружности и прямые, заданные уравнениями. |
-
|
|
| Решение задач на метод координат. | 1 | Тип: комбинированный Вид: смешанный | Записывать уравнения прямых и окружностей, использовать уравнения при решении задач, строить окружности и прямые, заданные уравнениями, строить окружности и прямые заданные уравнениями |
-
|
|
| Методы решения систем уравнений. | 1 | Тип: комбинированный Вид: смешанный | Знать алгоритм метода подстановки. Уметь использовать графики при решении системы уравнений, использовать для решения познавательных задач справочную литературу. Уметь: – при решении систем уравнений применять метод алгебраического сложения и метод введения новой переменной; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Методы решения систем уравнений. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Методы решения систем уравнений. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Решение задач на метод координат. | 1 | Тип: комбинированный Вид: практикум | Записывать уравнения прямых и окружностей, использовать уравнения при решении задач, строить окружности и прямые, заданные уравнениями, строить окружности и прямые заданные уравнениями |
-
|
|
| Контрольная работа по теме «Метод координат». | 1 | Тип: контроль знаний и умений Вид: контрольная работа |
|
-
|
|
| Методы решения систем уравнений. | 1 | Тип: комбинированный Вид: смешанный | Знать алгоритм метода подстановки. Уметь использовать графики при решении системы уравнений, использовать для решения познавательных задач справочную литературу. Уметь: – при решении систем уравнений применять метод алгебраического сложения и метод введения новой переменной; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Системы уравнений как математические модели реальных ситуаций | 1 | Тип: изучение нового материала Вид: беседа | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь: – составлять математические модели реальных ситуаций
и работать с составленной моделью; – приводить примеры, подбирать аргументы, формулировать выводы; – воспроизводить прочитанную информацию с заданной степенью свернутости; – извлекать необходимую информацию из учебно-научных текстов; – аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их. |
-
|
|
| Решение задач на движение с помощью систем уравнений. | 1 | Тип: комбинированный Вид: смешанный |
|
|
|
| Соотношения между сторонами и углами треугольника.
| 11 |
|
-
|
|
| Синус, косинус и тангенс угла. | 1 | Тип: комбинированный Вид: смешанный | Знать, как вычисляется синус, косинус, тангенс для углов от 0 до 180, уметь доказывать основное тригонометрическое тождество, знать формулу для вычисления координат точки, уметь решать задачи |
-
|
|
| Синус, косинус и тангенс угла. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Решение задач на совместную работу. | 1 | Тип: комбинированный Вид: практикум | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь: – составлять математические модели реальных ситуаций и работать с составленной моделью; – приводить примеры, подбирать аргументы, формулировать выводы; – воспроизводить прочитанную информацию с заданной степенью свернутости; – извлекать необходимую информацию из учебно-научных текстов; – аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их |
-
|
|
| Решение задач на совместную работу. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Системы уравнений как математические модели реальных ситуаций. | 1 | Тип: комбинированный Вид: консультация |
-
|
|
| Синус, косинус и тангенс угла. | 1 | Тип: комбинированный Вид: смешанный | Знать, как вычисляется синус, косинус, тангенс для углов от 0 до 180, уметь доказывать основное тригонометрическое тождество, знать формулу для вычисления координат точки, уметь решать задачи |
-
|
|
| Теорема о площади треугольника. Теоремы синусов и косинусов.
| 1 | Тип: комбинированный Вид: смешанный | Знать, как вычисляется синус, косинус, тангенс для углов от 0 до 180, уметь доказывать основное тригонометрическое тождество, знать формулу для вычисления координат точки, уметь решать задачи |
-
|
|
| Системы уравнений как математические модели реальных ситуаций. | 1 | Тип: повторительно-обобщающий Вид: семинар | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь: – составлять математические модели реальных ситуаций и работать с составленной моделью; – приводить примеры, подбирать аргументы, формулировать выводы; – воспроизводить прочитанную информацию с заданной степенью свернутости; – извлекать необходимую информацию из учебно-научных текстов; – аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их |
-
|
|
| Контрольная работа по теме «Системы уравнений». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь: – решать нелинейные системы уравнений двух переменных различными методами; – владеть навыками самоанализа и самоконтроля, контроля и оценки своей деятельности. |
|
|
|
| Числовые функции.
| 24 |
|
-
|
|
| Определение числовой функции. Область определения. Область значений функции. | 1 | Тип: изучение нового материала Вид: беседа | Знать определение числовой функции, области определения и области значения функции. Уметь: - находить область определения функции, объяснить изученные положения на самостоятельно подобранных конкретных примерах; – пользоваться навыками нахождения области определения функции, решая задания повышенной сложности |
-
|
|
| Решение треугольников. | 1 | Тип: комбинированный Вид: смешанный | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. |
-
|
|
| Решение треугольников. Измерительные работы. | 1 | Тип: комбинированный Вид: практикум
|
-
|
|
| Нахождение области определения и области значения функции. | 1 | Тип: изучение нового материала Вид: беседа | Знать определение числовой функции, области определения и области значения функции. Уметь: - находить область определения функции, объяснить изученные положения на самостоятельно подобранных конкретных примерах; – пользоваться навыками нахождения области определения функции, решая задания повышенной сложности |
-
|
|
| Кусочно-заданные функции. | 1 | Тип: изучение нового материала Вид: беседа |
-
|
|
| Решение упражнений на числовые функции. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Соотношения между сторонами и углами треугольника. | 1 | Тип: комбинированный Вид: смешанный | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами |
-
|
|
| Скалярное произведение векторов. | 1 | Тип: изучение нового материала Вид: беседа | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. |
-
|
|
| Способы задания функции. | 1 | Тип: изучение нового материала Вид: беседа | Иметь представление о способах задания функции: аналитическом, графическом, табличном, словесном. Уметь: – при задании функции применять различные способы: аналитический, графический, табличный, словесный; – отбирать и структурировать материал; – проводить анализ данного задания, аргументировать решение, презентовать решения |
-
|
|
| Способы задания функции. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Свойства функций. | 1 | Тип: изучение нового материала Вид: беседа | Иметь представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции,
ограниченности, выпуклости и непрерывности. Уметь: – исследовать функции на: монотонность, наибольшее
и наименьшее значение, ограниченность, выпуклость и непрерывность; – отбирать и структурировать материал; – аргументировано отвечать на поставленные вопросы, участвовать в диалоге |
-
|
|
| Скалярное произведение в координатах. | 1 | Тип: комбинированный Вид: смешанный | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. |
-
|
|
| Применение скалярного произведения векторов при решении задач. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Свойства функций | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции,
ограниченности, выпуклости и непрерывности. Уметь: – исследовать функции на: монотонность, наибольшее
и наименьшее значение, ограниченность, выпуклость и непрерывность; – отбирать и структурировать материал; – аргументировано отвечать на поставленные вопросы, участвовать в диалоге |
-
|
|
| Свойства функций. Чтение графиков функций. | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Свойства функций. | 1 | Тип: комбинированный Вид: практикум | Иметь представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции, ограниченности, выпуклости и непрерывности. Уметь: – исследовать функции на: монотонность, наибольшее
и наименьшее значение, ограниченность, выпуклость и непрерывность; – отбирать и структурировать материал; – аргументировано отвечать на поставленные вопросы, участвовать в диалоге |
-
|
|
| Контрольная работа по теме «Соотношения между сторонами и углами треугольника». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь применять полученные теоретические знания на практике |
|
|
|
| Длина окружности и площадь круга.
| 12 |
|
-
|
|
| Правильный многоугольник. | 1 | Тип: изучение нового материала Вид: беседа | Знать определение правильного многоугольника |
-
|
|
| Четные и нечетные функции. | 1 | Тип: изучение нового материала Вид: беседа | Иметь представление о понятии четной и нечетной функции, об алгоритме исследования функции на четность и нечетность. Уметь: – применять алгоритм исследования функции на четность и строить графики четных и нечетных функций; – приводить примеры, подбирать аргументы, формулировать выводы; – классифицировать и проводить сравнительный анализ |
-
|
|
| Четные и нечетные функции. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Четные и нечетные функции. | 1 | Тип: повторительно-обобщающий Вид: семинар |
-
|
|
| Окружность, описанная около правильного многоугольника и вписанная в правильный многоугольник. | 1 | Тип: комбинированный Вид: смешанный | Знать и уметь применять на практике теорему об окружности, описанной около правильного многоугольника и окружности, вписанной в правильный многоугольник |
-
|
|
| Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности | 1 | Тип: изучение нового материала Вид: лекция | Знать формулы для вычисления угла, площади и стороны правильного многоугольника и радиуса вписанной в него окружности, уметь их выводить и применять при решении задач типа |
-
|
|
| Контрольная работа по теме «Числовые функции. Способы задания функций и их свойства». | 1 | Тип: комбинированный Тип: контроль знаний и умений Вид: контрольная работа | Уметь: самостоятельно находить область определения функции, объяснить изученные положения на самостоятельно подобранных конкретных примерах; – пользоваться навыками нахождения области определения функции, решая задания повышенной сложности |
-
|
|
| Функции у=хn( nєN), их свойства и графики. | 1 | Тип: изучение нового материала Вид: беседа | Иметь представление о понятии степенной функции
с натуральным показателем, о свойствах и графике функции. Знать о понятии степенной функции с натуральным показателем, о свойствах и графике функции. Уметь: – определять графики функций с четным и нечетным показателем; – оформлять решения или сокращать решения, в зависимости от ситуации |
-
|
|
| Функции у=хn( nєN), их свойства и графики. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Решение задач по теме «Правильный многоугольник». | 1 | Тип: комбинированный Вид: смешанный | Доказывать теоремы об окружности вписанной и описанной. Выводить и применять при решении задач формулы площади. Строить правильные многоугольники |
-
|
|
| Длина окружности. | 1 | Тип: комбинированный Вид: смешанный | Знать формулы длины окружности и дуги окружности, уметь применять их при решении задач |
-
|
|
| Функции у=хn( nєN), их свойства и графики. | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о понятии степенной функции
с натуральным показателем, о свойствах и графике функции. Знать о понятии степенной функции с натуральным показателем, о свойствах и графике функции. Уметь: – определять графики функций с четным и нечетным показателем; – оформлять решения или сокращать решения, в зависимости от ситуации |
-
|
|
| Функции у=х - n( nєN), их свойства и графики. | 1 | Тип: изучение нового материала Вид: беседа |
-
|
|
| Функции у=х - n( nєN), их свойства и графики. | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о понятии степенной функции с отрицательным целым показателем, о свойствах и графике функции. Знать о понятии степенной функции с отрицательным целым показателем, о свойствах
и графике функции. Уметь: – определять графики функций с четным и нечетным отрицательным целым показателем; – оформлять решения, выполнять задания по заданному алгоритму, участие в диалоге; – строить графики степенных функций с любым показателем степени; – читать свойства по графику функции; – строить графики функций по описанным свойствам |
-
|
|
| Длина окружности. Решение задач. | 1 | Тип: комбинированный Вид: практикум | Знать формулы длины окружности и дуги окружности, уметь применять их при решении задач |
-
|
|
| Площадь круга и кругового сектора. | 1 | Тип: изучение нового материала Вид: беседа | Знать формулы площади круга и кругового сектора, уметь применять их при решении задач |
-
|
|
| Функции у=х - n( nєN), их свойства и графики. | 1 | Тип: комбинированный Вид: практикум | Иметь представление о понятии степенной функции с отрицательным целым показателем, о свойствах и графике функции. Знать о понятии степенной функции с отрицательным целым показателем, о свойствах
и графике функции. Уметь: – определять графики функций с четным и нечетным отрицательным целым показателем; – оформлять решения, выполнять задания по заданному алгоритму, участие в диалоге; – строить графики степенных функций с любым показателем степени; – читать свойства по графику функции; – строить графики функций по описанным свойствам |
-
|
|
| Функция у =  , её свойства и график | 1 | Тип: изучение нового материала Вид: беседа |
-
|
|
| Функция у = 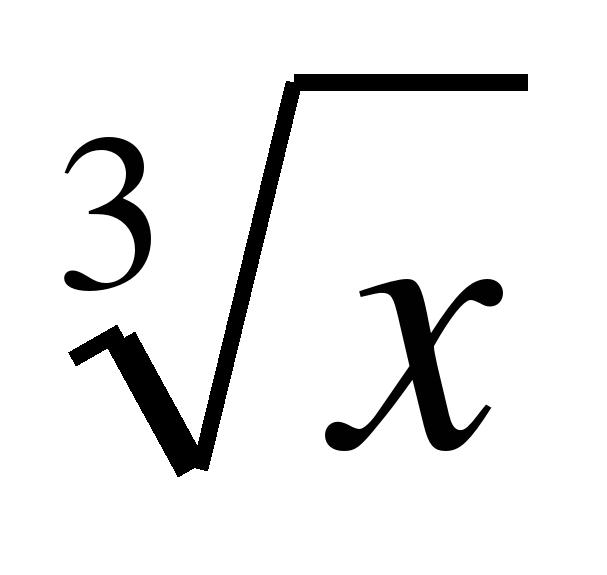 , её свойства и график | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Площадь круга и кругового сектора. | 1 | Тип: комбинированный Вид: смешанный | Знать формулы площади круга и кругового сектора, уметь применять их при решении задач |
-
|
|
| Длина окружности. Площадь круга. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Функция у = 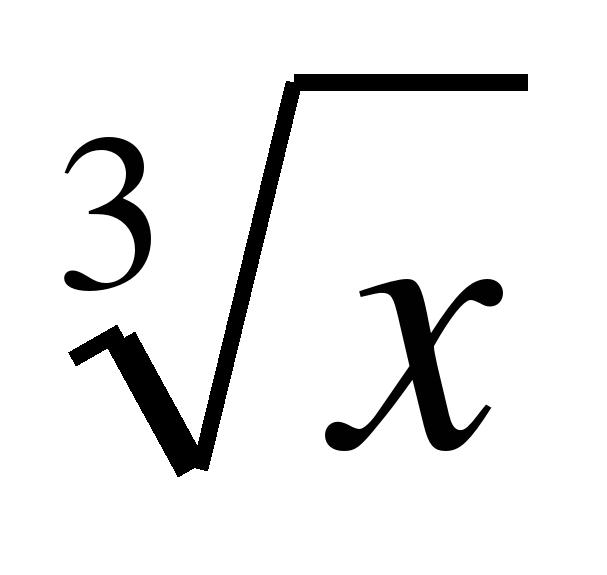, её свойства и график | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о понятии степенной функции с отрицательным целым показателем, о свойствах и графике функции. Знать о понятии степенной функции с отрицательным целым показателем, о свойствах
и графике функции. Уметь: – определять графики функций с четным и нечетным отрицательным целым показателем; – оформлять решения, выполнять задания по заданному алгоритму, участие в диалоге; – строить графики степенных функций с любым показателем степени; – читать свойства по графику функции; – строить графики функций по описанным свойствам |
-
|
|
| Контрольная работа по теме «Функции у=хn( nєN), их свойства и графики». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь: – строить и описывать свойства элементарных функций; – владеть навыками самоанализа
и самоконтроля; – предвидеть возможные последствия своих действий |
|
|
|
| Прогрессии. | 14 |
|
-
|
|
| Определение числовой последовательности | 1 | Тип: изучение нового материала Вид: беседа | Иметь представление о способах задания числовой последовательности. Знать определение числовой последовательности. Уметь: – задавать числовую последовательность аналитически, словесно, рекуррентно; – привести примеры числовых последовательностей; – определять понятия, приводить доказательства; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Решение задач на длину окружности и площадь круга. | 1 | Тип: комбинированный Вид: практикум | Знать формулы площади круга и кругового сектора, уметь применять их при решении задач |
-
|
|
| Решение задач на длину окружности и площадь круга. | 1 | Тип: комбинированный Вид: консультация |
-
|
|
| Числовые последовательности и способы их задания. | 1 | Тип: изучение нового материала Вид: беседа | Иметь представление о способах задания числовой последовательности. Знать определение числовой последовательности. Уметь: – задавать числовую последовательность аналитически, словесно, рекуррентно; – привести примеры числовых последовательностей; – определять понятия, приводить доказательства; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Числовые последовательности и их свойства. | 1 | Тип: комбинированный Вид: смешанный |
-
|
|
| Арифметическая прогрессия | 1 | Тип: изучение нового материала Вид: беседа | Иметь представление о правиле задания арифметической прогрессии, формуле n-го члена арифметической прогрессии, формуле суммы членов конечной арифметической прогрессии. Знать правило
и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; характеристическое свойство арифметической прогрессии и применение его при решении математических задач. Уметь: – применять формулы при решении задач; – обосновывать суждения |
-
|
|
| Контрольная работа по теме «Длина окружности и площадь круга». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь применять полученные теоретические знания на практике |
|
|
|
| Движения.
| 8 |
|
-
|
|
| Понятие движения. | 1 | Тип: изучение нового материала Вид: беседа | Уметь объяснить, что такое отображение плоскости на себя, знать определение движения плоскости Знать, уметь применять свойства движений на практике; доказывать, что осевая и центральная симметрия являются движениями. Уметь решать задачи с применением движений. |
-
|
|
| Арифметическая прогрессия. | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о правиле задания арифметической прогрессии, формуле n-го члена арифметической прогрессии, формуле суммы членов конечной арифметической прогрессии. Знать правило
и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; характеристическое свойство арифметической прогрессии и применение его при решении математических задач. Уметь: – применять формулы при решении задач; – обосновывать суждения |
-
|
|
| Формула суммы членов конечной арифметической прогрессии. | 1 | Тип: изучение нового материала Вид: беседа |
-
|
|
| Характеристическое свойство арифметической прогрессии. | 1 | Тип: изучение нового материала Вид: беседа |
-
|
|
| Свойства движений. | 1 | Тип: комбинированный Вид: смешанный | Уметь объяснить, что такое отображение плоскости на себя, знать определение движения плоскости Знать, уметь применять свойства движений на практике; доказывать, что осевая и центральная симметрия являются движениями. Уметь решать задачи с применением движений. |
-
|
|
| Решение задач по теме «Понятие движения. Осевая и центральная симметрии». | 1 | Тип: комбинированный Вид: практикум |
-
|
|
| Арифметическая прогрессия. | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о правиле задания арифметической прогрессии, формуле n-го члена арифметической прогрессии, формуле суммы членов конечной арифметической прогрессии. Знать правило
и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; характеристическое свойство арифметической прогрессии и применение его при решении математических задач. Уметь: – применять формулы при решении задач; – обосновывать суждения |
-
|
|
| Определение геометрической прогрессии. | 1 | Тип: изучение нового материала Вид: беседа | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии; характеристическое свойство геометрической прогрессии и применение его при решении математических задач. Уметь: – применять формулы при решении задач; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Формула n- го члена геометрической прогрессии. | 1 | Тип: изучение нового материала Вид: беседа |
-
|
|
| Параллельный перенос. | 1 | Тип: изучение нового материала Вид: смешанный | Уметь объяснять, что такое параллельный перенос и поворот, доказывать, что параллельный перенос и поворот являются движениями плоскости; строить образы фигур при симметриях, параллельном переносе и повороте. |
-
|
|
| Поворот. | 1 | Тип: изучение нового материала Вид: смешанный |
-
|
|
| Формула суммы членов геометрической прогрессии. | 1 | Тип: изучение нового материала Вид: смешанный | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии; характеристическое свойство геометрической прогрессии и применение его при решении математических задач. Уметь: – применять формулы при решении задач; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Характеристическое свойство геометрической прогрессии. | 1 | Тип: изучение нового материала Вид: смешанный |
-
|
|
| Геометрическая прогрессия. | 1 | Тип: комбинированный Вид: смешанный | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии; характеристическое свойство геометрической прогрессии и применение его при решении математических задач. Уметь: – применять формулы при решении задач; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Решение задач по теме «Параллельный перенос. Поворот». | 1 | Тип: комбинированный Вид: практикум | Уметь решать задачи с применением движений. |
-
|
|
| Решение задач на движение. | 1 | Тип: комбинированный Вид: консультация | Уметь решать задачи с применением движений. |
-
|
|
| Контрольная работа по теме «Прогрессии». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь: – решать задания на применение свойств арифметической
и геометрической прогрессии; – владеть навыками самоанализа и самоконтроля; – владеть навыками контроля и оценки своей деятельности |
|
|
|
| Элементы комбинаторики, статистики и теории вероятности. | 20 |
|
-
|
|
| Комбинаторные задачи
| 1 | Тип: комбинированный Вид: смешанный | Иметь представление о понятии перебора вариантов. Уметь приводить примеры, подбирать аргументы, формулировать выводы |
-
|
|
| Комбинаторные задачи | 1 | Тип: комбинированный Вид: практикум | Знать, как построить дерево возможных вариантов для небольшого количества вариантов. Уметь составить таблицу значений, обосновывать суждения Иметь представление о правиле умножения. Уметь выбрать
и выполнить задание по своим силам и знаниям, применить знания для решения практических задач |
-
|
|
| Контрольная работа по теме «Движение». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь решать задачи с применением движений. |
|
|
|
| Начальные сведения из стереометрии.
| 8 |
|
-
|
|
| Многогранники | 1 | Тип: комбинированный Вид: смешанный | Знать определения геометрического тела; границы тела; уметь находить и называть на моделях и чертежах элементы геом. тел; изображать объемные фигуры и их развертки на клетч. бумаге |
-
|
|
| Комбинаторные задачи
| 1 | Тип: комбинированный Вид: проблемное изложение | Иметь представление о треугольнике Паскаля, о событиях достоверных, невозможных, случайных; о классической вероятностной схеме, классическим определением вероятности. Уметь пользоваться формулой вычисления вероятности, решать задачи на характеристику событий. |
-
|
|
| Комбинаторные задачи | 1 | Тип: комбинированный Вид: практикум | Иметь представление о факториале, используя правило умножения. Уметь отбирать
и структурировать материал, передавать, информацию сжато, полно, выборочно |
-
|
|
| Комбинаторные задачи | 1 | Тип: комбинированный Вид: практикум с элементами исследования | Знать, как на конкретных примерах рассмотреть основные методы решения простейших комбинаторных задач. Уметь вывести некоторые свойства синуса, косинуса, тангенса, определять понятия, приводить доказательства |
-
|
|
| Многогранники | 1 | Тип: комбинированный Вид: смешанный | Знать определение призмы; формулы площади поверхности и объема; применять эти формулы к решению задач |
-
|
|
| Многогранники | 1 | Тип: комбинированный Вид: смешанный | Знать определения прямоуг. параллелепипеда и куба; свойства прямоуг. параллелепипеда и куба; решать задачи на вычисление площади поверхности и объема и нахождение элементов многогранников |
-
|
|
| Комбинаторные задачи | 1 | Тип: комбинированный Вид: практикум |
|
-
|
|
| Статистика – дизайн информации | 1 | Тип: изучение нового материала Вид: смешанный | Иметь представление об основных понятиях статистического исследования; приводить примеры, подбирать аргументы, формулировать выводы, передавать информацию сжато, полно, выборочно |
-
|
|
| Статистика – дизайн информации |
| Тип: комбинированный Вид: практикум | Иметь представление о группировке информации. Уметь отбирать и структурировать материал, использовать для решения познавательных задач справочную литературу, выбрать и выполнить задание по своим силам и знаниям |
-
|
|
| Многогранники | 1 | Тип: комбинированный Вид: смешанный | Знать определения прямоуг. параллелепипеда и куба; свойства прямоуг. параллелепипеда и куба; решать задачи на вычисление площади поверхности и объема и нахождение элементов многогранников |
-
|
|
| Тела и поверхности вращения | 1 | Тип: комбинированный Вид: смешанный | Знать определения цилиндра и конуса и их элементы; решать задачи на вычисление площади поверхности и объема и нахождение элементов тел вращения. Определять понятия шара и сферы; знать определения шарового сектора и сегмента; знать формулы площади поверхности и объема и применять их при решении задач |
-
|
|
| Статистика – дизайн информации | 1 | Тип: комбинированный Вид: смешанный | Уметь представлять информацию о распределении данных таблично, объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Статистика – дизайн информации | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о графическом представлении информации.
Уметь работать по заданному алгоритму, выполнять и оформлять тестовые задания, сопоставлять предмет и окружающий мир, применить знания для решения практических задач |
-
|
|
| Статистика – дизайн информации | 1 | Тип: комбинированный Вид: практикум | Иметь представление о простейших числовых характеристиках информации, полученной при проведении эксперимента, которые вместе с другими данными образуют своего рода паспорт результатов этого эксперимента |
-
|
|
| Тела и поверхности вращения | 1 | Тип: комбинированный Вид: смешанный | Знать определения цилиндра и конуса и их элементы; решать задачи на вычисление площади поверхности и объема и нахождение элементов тел вращения. Определять понятия шара и сферы; знать определения шарового сектора и сегмента; знать формулы площади поверхности и объема и применять их при решении задач |
-
|
|
| Тела и поверхности вращения | 1 | Тип: комбинированный Вид: смешанный | Знать определения цилиндра и конуса и их элементы; решать задачи на вычисление площади поверхности и объема и нахождение элементов тел вращения. Определять понятия шара и сферы; знать определения шарового сектора и сегмента; знать формулы площади поверхности и объема и применять их при решении задач |
-
|
|
| Решение заданий по теме «Элементы комбинаторики и статистики» | 1 | Тип: комбинированный Вид: практикум | Уметь на конкретных примерах использовать основные методы решения простейших комбинаторных задач, приводить примеры, подбирать аргументы, формулировать выводы, составлять текст научного стиля |
-
|
|
| Простейшие вероятностные задачи | 1 | Тип: комбинированный Вид: смешанный | Иметь представление об основных видах случайных событий: достоверное, невозможное, несовместимое события. Уметь выбрать и выполнить задание по своим силам |
-
|
|
| Простейшие вероятностные задачи | 1 | Тип: комбинированный Вид: практикум | Иметь представление о событии, противоположном данному событию, о сумме двух случайных событий. Уметь обосновывать суждения, выполнять и оформлять тестовые задания, подбирать аргументы для обоснования найденной ошибки |
-
|
|
| Тела и поверхности вращения | 1 | Тип: обобщения и систематизации знаний Вид: семинар | Применять ЗУН для решения задач повыш. уровня и с практическим содержанием |
-
|
|
| Простейшие вероятностные задачи | 1 | Тип: комбинированный Вид: смешанный | Уметь вычислять достоверное, невозможное, несовместимое события, объяснять изученные положения на самостоятельно подобранных примерах |
-
|
|
| Экспериментальные данные и вероятности событий | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о модели реальности, о статистической устойчивости и о статистической вероятности события. Уметь объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Экспериментальные данные и вероятности событий | 1 | Тип: комбинированный Вид: смешанный | Иметь представление об эмпирических испытаниях, о частотных таблицах. Уметь воспринимать устную речь, участвовать в диалоге, проводить сравнительный анализ, сопоставлять, рассуждать |
-
|
|
| Экспериментальные данные и вероятности событий | 1 | Тип: комбинированный Вид: смешанный | Иметь представление о теоретической вероятности. Уметь извлекать необходимую информацию из учебно-научных текстов, объяснить изученные положения на самостоятельно подобранных примерах |
-
|
|
| Решение заданий по теме «Элементы теории вероятностей» | 1 | Тип: комбинированный Вид: практикум | Уметь решать простейшие вероятностные задачи, объяснить изученные положения на самостоятельно подобранных примерах |
-
|
|
| Контрольная работа по теме «События, вероятности, статистическая обработка данных». | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Уметь решать самостоятельно простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения. |
-
|
|
| Об аксиомах планиметрии. | 1 | Тип: комбинированный Вид: смешанный | Знать аксиомы планиметрии |
-
|
|
| Об аксиомах планиметрии. | 1 | Тип: комбинированный Вид: смешанный | Знать аксиомы планиметрии |
|
|
|
| Повторение.
| 13 |
|
-
|
|
| Неравенства и системы неравенств. | 1 | Тип: повторительно-обобщающий Вид: практикум | Уметь: – решать рациональные неравенства и системы рациональных неравенств; – приводить примеры, подбирать аргументы, формулировать выводы; – составлять текст научного стиля |
-
|
|
| Неравенства и системы неравенств. | 1 | Тип: повторительно-обобщающий Вид: практикум |
-
|
|
| Системы уравнений. | 1 | Тип: повторительно-обобщающий Вид: практикум | Уметь: – решать нелинейные системы уравнений двух переменных различными методами; – объяснить изученные положения на самостоятельно подобранных конкретных примерах |
-
|
|
| Числовые функции. | 1 | Тип: повторительно-обобщающий Вид: семинар | Уметь: – строить и описывать свойства элементарных функций; – определять понятия, приводить доказательства; – найти и устранить причины возникших трудностей |
-
|
|
| Прогрессии. | 1 | Тип: комбинированный Вид: смешанный | Уметь: – решать задания на применение свойств арифметической и геометрической прогрессии; – извлекать необходимую информацию из учебно-научных текстов; – отделить основную информацию от второстепенной. |
-
|
|
| Прогрессии. | 1 | Тип: повторительно-обобщающий Вид: практикум |
-
|
|
| Треугольники | 1 | Тип: повторительно-обобщающий Вид: практикум | Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. |
-
|
|
| Окружность. | 1 | Тип: комбинированный Вид: смешанный | Уметь применять формулы длины окружности и дуги окружности и формулы площади круга и кругового сектора при решении задач |
-
|
|
| Векторы. Метод координат. | 1 | Тип: комбинированный Вид: смешанный | Уметь решать задачи на применение законов сложения, вычитания векторов, умножения вектора на число |
-
|
|
| Итоговая контрольная работа | 1 | Тип: контроль знаний и умений Вид: контрольная работа | Учащиеся демонстрируют умение обобщения и систематизации знаний по основным темам курса алгебры 9 класса. Владеют навыками самоанализа и самоконтроля |
-
|
|
| Векторы. Метод координат. | 1 | Тип: комбинированный Вид: смешанный | Уметь решать задачи на применение законов сложения, вычитания векторов, умножения вектора на число |
-
|
|
| Соотношения между сторонами и углами треугольника | 1 | Тип: комбинированный Вид: смешанный | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами |
-
|
|
| Соотношения между сторонами и углами треугольника | 1 | Тип: комбинированный Вид: смешанный |
Получите свидетельство
Вход
, 
.
Рабочая программа по учебному предмету "Математика" (9 класс) (0.57 MB)
0
519
15
Нравится
0
