Рабочая программа
по математике за курс 8 класса
базовый уровень на 2015-2016 уч.г.
Структура программы
Рабочая программа содержит следующие разделы:
Титульный лист.
Пояснительную записку;
Статус документа (на основе чего составлена программа);
Место в базисном учебном плане (сколько часов в неделю, в год);
Цели и задачи;
Общая характеристика предмета;
Требования к уровню подготовки обучающихся.
Содержание образования по предмету.
Тематическое планирование.
Контрольно-измерительные материалы.
Календарно-тематическое планирование.
Учебно-методический комплекс.
Нормы оценок.
Материально-техническое обеспечение.
Пояснительная записка
Статус документа
Рабочая программа учебного предмета «Математика – 8» (далее Рабочая программа) составлена на основании:
- Программы. Математика. 5-6 классы Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы/ авт.-сост. И.И. Зубарева, А.Г, Мордкович. – 2-е изд., испр. и доп.. – М.: Мнемозина, 2009. – 63 с.).,
- Программы общеобразовательных учреждений по геометрии 7–9 классы, к учебному комплексу для 7-9 классов, авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др., составитель Т.А. Бурмистрова – М: «Просвещение», 2008 – М: «Просвещение», 2008. – с. 19-21.
Программа соответствует учебникам:
- Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Н. П. Николаев. — М. : Мнемозина, 2009. — 191 с., Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — 13-е изд., испр. и доп. — М.: Мнемозина, 2009. — 270 с.,
- Геометрия, 7—9 классы: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и д. — М.: Просвещение, 2009
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса.
Программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Место предмета в базисном учебном плане
Программа составлена на основе Базисного учебного плана 2004 г. и рассчитана на 175 часов в год (5 часов в неделю), из них 105 часов (3 часа в неделю) – «Алгебра», 70 часов (2 часа в неделю) – «Геометрия».
С учетом требований Федерального государственного образовательного стандарта основного общего образования в содержании рабочей программы предполагается реализовать компетентностный, личностно ориентированный и деятельностный подходы, которые определяют задачи обучения: приобретение математических знаний и умений; освоение универсальных учебных действий.
Компетентностный подход определяет следующие особенности предъявления содержания образования: оно представлено в виде трех тематических блоков, обеспечивающих формирование компетенций. В первом блоке представлены дидактические единицы, обеспечивающие совершенствование математических навыков. Во втором – дидактические единицы, которые содержат сведения из истории математики. Это содержание обучения является базой для развития коммуникативной компетенции учащихся. В третьем блоке представлены дидактические единицы, отражающие информационную компетенцию и обеспечивающие развитие учебно-познавательной и рефлексивной компетенций. Таким образом, рабочая программа обеспечивает взаимосвязанное развитие и совершенствование ключевых, общепредметных и предметных компетенций.
Принципы отбора содержания связаны с преемственностью целей образования на различных ступенях и уровнях обучения, логикой внутрипредметных связей, а также с возрастными особенностями развития учащихся.
Личностная ориентация образовательного процесса выявляет приоритет воспитательных и развивающих целей обучения. Способность учащихся понимать причины и логику развития математических процессов открывает возможность для осмысленного восприятия всего разнообразия мировоззренческих, социокультурных систем, существующих в современном мире. Система учебных занятий призвана способствовать развитию личностной самоидентификации, гуманитарной культуры школьников, их приобщению к естественно-математической культуре, усилению мотивации к социальному познанию и творчеству, воспитанию личностно и общественно востребованных качеств, в том числе гражданственности, толерантности.
Деятельностный подход отражает стратегию современной образовательной политики: необходимость воспитания человека и гражданина, интегрированного в современное ему общество, нацеленного на совершенствование этого общества. Система уроков сориентирована не столько на передачу готовых знаний, сколько на формирование активной личности, мотивированной к самообразованию, обладающей достаточными навыками и психологическими установками к самостоятельному поиску, отбору, анализу и использованию информации. Это поможет выпускнику адаптироваться в мире, где объем информации растет в геометрической прогрессии, где социальная и профессиональная успешность напрямую зависят от позитивного отношения к новациям, самостоятельности мышления и инициативности, от готовности проявлять творческий подход к делу, искать нестандартные способы решения проблем, конструктивно взаимодействовать с людьми.
Основой целеполагания является обновление требований к уровню подготовки выпускников в системе естественно-математического образования, отражающее важнейшую особенность педагогической концепции государственного стандарта – переход от суммы «предметных результатов» ( то есть образовательных результатов, достигаемых в рамках отдельных учебных предметов), к межпредметным и интегративным результатам. Такие результаты представляют собой обобщенные способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как универсальные учебные действия, что предполагает повышенное внимание к развитию межпредметных связей курса математики.
Дидактическая модель обучения и педагогические средства отражают модернизацию основ учебного процесса, их переориентацию на достижение конкретных результатов в виде сформированных регулятивных, коммуникативных и познавательных учебных умений. Формирование целостных представлений о математике будет осуществляться в ходе творческой деятельности учащихся на основе личностного осмысления математических фактов и явлений. Особое внимание уделяется познавательной активности учащихся, их мотивированности к самостоятельной учебной работе. Это предполагает все более широкое использование нетрадиционных форм уроков, в том числе методики деловых и ролевых игр, проблемных дискуссий, межпредметных интегрированных уроков и т.д.
Планируется использование следующих технологий в преподавании предмета:
Технологии полного усвоения;
Технологии обучения на основе решения задач;
Технологии обучения на основе схематических и новых знаковых моделей.
Для естественно – математического образования приоритетным можно считать развитие умений самостоятельно и мотивированно организовывать свою познавательную деятельность, использовать элементы причинно-следственного и структурно-функционального анализа, определять сущностные характеристики изучаемого объекта, самостоятельно выбирать критерии для сравнения, сопоставления, оценки и классификации объектов – в программе это является основой для целеполагания.
На ступени основной школы задачи учебных занятий (в схеме – планируемый результат) определены как закрепление умений разделять процессы на этапы, звенья, выделять характерные причинно – следственные связи, определять структуру объекта познания, значимые функциональные связи и отношения между частями целого, сравнивать, сопоставлять, классифицировать, ранжировать объекты по одному или нескольким предложенным основаниям, критериям. Принципиальное значение в рамках курса приобретает умение различать факты, мнения, доказательства, гипотезы, аксиомы.
При выполнении творческих работ формируется умение определять адекватные способы решения учебных задач на основе заданных алгоритмов, комбинировать известные алгоритмы деятельности в ситуациях, не предполагающих стандартного применения одного из них, мотивированно отказываться от образца деятельности, искать оригинальные решения.
Учащиеся должны приобрести умения по формированию собственного алгоритма решения познавательных задач, уметь формулировать проблему и цели своей работы, определять адекватные способы и методы решения задачи, прогнозировать ожидаемый результат и сопоставлять его с собственными математическими знаниями. Учащиеся должны научиться представлять результаты индивидуальной и групповой познавательной деятельности в формах конспекта, реферата, рецензии.
Реализация рабочей программы обеспечивает освоение коммуникативных учебных действий, в том числе способностей передавать содержание текста в сжатом и развернутом виде в соответствии с целью учебного задания, проводить информационно-смысловой анализ текста, составлять план, тезисы, конспект. На уроках учащиеся более уверенно овладеют монологической и диалогической речью, умением вступать в речевое общение, участвовать в диалоге ( понимать точку зрения собеседника, признавать право на иное мнение), научатся приводить примеры, подбирать аргументы, перефразировать мысль, формулировать выводы. Для решения познавательных и коммуникативных задач учащимся предлагается использовать различные источники информации, включая энциклопедии, словари, Интернет-ресурсы и другие базы данных, в соответствии с коммуникативной задачей, сферой и ситуацией общения осознанно выбирать выразительные средства языка и знаковые системы.
В процессе обучения должно быть сформировано умение формулировать свои мировоззренческие взгляды как основа духовно-нравственного развития школьника.
Цели и задачи изучения
Изучение математики в основной школе направлено на достижение следующих целей:
В направлении личностного развития:
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
Формирование качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
Развитие интереса к математическому творчеству и математических способностей;
В метапредметном направлении:
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
Развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
В предметном направлении:
Овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, для изучения смежных дисциплин, применения в повседневной жизни;
Создание фундамента математического развития, формирования механизмов мышления, характерных для математической деятельности.
Общая характеристика учебного предмета.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
В ходе освоения содержания курса учащиеся получают возможность:
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить логическое мышление и речь — умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В ходе преподавания алгебры в 8 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Требования к уровню подготовки учащихся 8 класса
В результате изучения алгебры ученик должен
Знать/понимать:
значение математической науки для решения задач, возникающих в теории и практике;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа;
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени;
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные выражения рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним системы двух линейных уравнений и несложные нелинейные уравнения;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученные результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
В результате изучения геометрии ученик должен
Уметь:
распознавать геометрические фигуры, различать их взаимное расположение;
выполнять чертежи по условиям задач;
изображать геометрические фигуры; осуществлять преобразования фигур;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения,
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования несложных практических ситуаций на основе изученных формул и свойств фигур;
вычислений площадей фигур при решении практических задач.
Требования к ЗУН представлены и в тематическом плане по каждой теме.
решать следующие жизненно-практические задачи:
самостоятельно приобретать и применять знания в различных ситуациях;
работать в группах;
аргументировать и отстаивать свою точку зрения;
уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем энциклопедий и справочников для нахождения информации
Владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной;
Быть способным решать следующие жизненно-практические задачи: самостоятельно приобретать и применять знания в различных ситуациях, работать в группе, аргументировать и отстаивать свою точку зрения, уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов; пользоваться предметным указателем, энциклопедией и справочником для нахождения информации; самостоятельно действовать в ситуации неопределенности при решении актуальных для учащихся проблем.
Содержание программы направлено на освоение учащимися знаний, умений и навыков на базовом уровне, что соответствует Образовательной программе школы.
Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике и авторской программой учебного курса.
Промежуточная аттестация проводится в форме контрольных, самостоятельных работ, математических диктантов, тестов.
Итоговая аттестация предусмотрена в виде административной контрольной работы.
Содержание тем учебного курса 8 класса
Алгебраические дроби
В результате изучения главы учащиеся должны:
Знать и уметь:
Понятие алгебраической дроби; Уметь находить допустимые значения дробных выражений; применять основное свойство дроби при любых значениях переменной, при которых знаменатель дроби отличен от нуля; Уметь складывать, умножать, делить и вычитать дробные выражения, возводить дробь в степень, применяя при необходимости формулы сокращенного умножения;
Уметь преобразовывать рациональные выражения, применяя формулы сокращенного умножения;
Уметь решать простейшие рациональные уравнения.
Повторить:
Формулы сокращенного умножения;
Способы разложения многочлена на множители; понятие тождества, тождественного преобразования, способ группировки;
Основное свойство дроби для обыкновенных дробей, правило сложения, умножения, деления и вычитания дробей.
Квадратичная функция. Функция у= к\х
В результате изучения главы учащиеся должны:
Знать и уметь:
Функцию у= кх2 , ее свойства, график, Понятие обратной пропорциональности, ее области определения; Уметь находить значение функции и аргумента по формуле y=k/x, строить график обратной пропорциональности и читать его; Построение графиков функций с помощью параллельного переноса по известному графику у= кх2 Квадратный трехчлен, квадратичная функция, ее свойства и график. Понятие ограниченной функции, построение и чтение графиков кусочных функций; Уметь графически решать квадратные уравнения.
Повторить:
Понятие функции, графика функции.
Функция у = √х. Свойства квадратного корня
В результате изучения главы учащиеся должны:
Знать и уметь:
Понятие квадратного корня из числа а и арифметического корня из числа а; знать его свойства и уметь применять их к нахождению значений квадратного корня из произведения, дроби и степени;
Уметь решать уравнение х2= а; Уметь строить график функции у = √х, знать некоторые свойства (выпуклость, область значений) этой функции, уметь по графику функции находить значения у и х, сравнивать числа, используя свойства функции; Знать тождество √х2=\х\ и уметь доказывать его;
Уметь выносить множитель из-под знака корня и вносить множитель под знак корня, применять эти умения при тождественных преобразованиях выражений, содержащих квадратные корни;
Уметь сокращать дроби, используя преобразование квадратных корней.
Повторить:
Построение графиков функции по координатам точек;
Правила умножения одночлена на многочлен и умножения многочлена на многочлен;
Формулы сокращенного умножения.
Квадратные уравнения
В результате изучения главы учащиеся должны:
Знать и уметь:
Определение квадратного уравнения, приведенного и неприведенного, полного и неполного квадратного уравнения и их решения; Уметь решать неполные квадратные уравнения методом разложения на множители, методом выделения полного квадрата; Знать формулу корней для решения квадратного уравнения и формулу для решения квадратных уравнений с четным вторым коэффициентом и решать полные квадратные уравнения с помощью формул;
Решать простейшие уравнения с параметром; Составлять математические модели реальных ситуаций с помощью квадратных уравнений, рациональных уравнений и дробных рациональных уравнений; Знать теорему Виета и обратную теореме Виета для решения приведенных квадратных уравнений; Понятие иррациональных уравнений и уметь их решать методом возведения в квадрат;
Понятие рациональных уравнений и их решения; Понятие биквадратного уравнения и его решение методом введения новой переменной.
Повторить:
Решение линейных уравнений.
Действительные числа
В результате изучения главы учащиеся должны:
Знать и уметь:
Понятие множества рациональных чисел и иррациональных чисел, понятие множества действительных чисел; Уметь представлять рациональное число в виде бесконечной десятичной периодической дроби, сравнивать рациональные числа;
Неравенства
В результате изучения главы учащиеся должны:
Знать и уметь:
Понятие числовых неравенств и использовать это определение при доказательстве неравенств;
Знать теоремы, выражающие свойства числовых неравенств, уметь применять их при выполнении упражнений, при оценке значений выражений; Теоремы о почленном сложении и умножении числовых неравенств, применять их для оценки суммы, разности, произведения и частного числовых неравенств; Понятие числового промежутка, уметь их изображать на координатной прямой, уметь изображать промежуток и множество чисел, удовлетворяющих неравенству, находить пересечение и объединение промежутков, используя координатную прямую;
Определение решения неравенства с одной переменной, равносильных неравенств; Знать свойства неравенств, используемых при решении неравенств и уметь их применять при решении неравенств;
Определение решения системы неравенств с одной переменной и уметь решать системы неравенств и двойные неравенства.
Повторить:
Правила сравнения любых чисел.
Четырехугольники.
В результате изучения главы учащиеся должны:
Знать и уметь:
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии. Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости состоится в 9 классе.
Повторить:
Признаки равенства треугольников.
Площадь.
В результате изучения главы учащиеся должны:
Знать и уметь:
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора, обратная теореме Пифагора.
Повторить: понятие площади, формулы нахождения площади прямоугольника, квадрата, треугольника.
3. Подобные треугольники.
В результате изучения главы учащиеся должны:
Знать и уметь:
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Повторить: признаки равенства треугольниов, понятие равных по площади фигур и углов, соотношения в прямоугльном треугольнике
4. Окружность.
В результате изучения главы учащиеся должны:
Знать и уметь:
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Повторить: основные понятия окружности: радиус, диаметр, хорда
5. Повторение. Решение задач
Учебно-тематическое планирование курса
математики 8 класс.
Количество часов по программе -175ч, в неделю - 5 часов, что соответствует федеральному компоненту базисного учебного плана.
Плановых контрольных работ - 14.
Учебно–тематический план:
| № | Темы программы | Кол-во часов | К/Р |
| 1. | Повторение курса математики 7 класса | 5 | 1 |
| 2. | Алгебраические дроби | 20 | 2 |
| 3. | Четырехугольники | 14 | 1 |
| 4. | Функция y=√x. Свойства квадратного корня | 19 | 1 |
| 5. | Площади фигур | 16 | 1 |
| 6. | Квадратичная функция. Функция у = к/х | 18 | 2 |
| 7. | Подобные треугольники | 20 | 2 |
| 8. | Квадратные уравнения | 21 | 2 |
| 9. | Окружность | 17 | 1 |
| 10 | Неравенства | 15 | 1 |
|
| Итоговое повторение курса 8 класса | 10 | 1 |
| ИТОГО 175 | 14 |
Учебно-тематическое планирование
по математике 8 класс
Условные обозначения
Тип урока:
УИНМ – урок изучения нового материала
КУ – комбинированный урок
УЗЗ – урок закрепления знаний (комплексного применения знаний)
УК – урок контроля
УОИСЗУ– урок обобщения и систематизации знаний и умений
| №п/п | Тема урока
| Тип урока | Элементы содержания |
Планируемые результаты освоения системы знаний обучающимися | Примечание |
| 1-5 | Повторение курса математики 7 класса 5ч |
|
| Раздел 1. Алгебраические дроби 20ч |
| 6 | Основные понятия алгебраической дроби | УИНМ | Понятие алгебраической дроби, множество допустимых значений переменной алгебраические дроби | Уметь распознать алгебраические дроби, находить множество допустимых значений переменной алгебраической дроби |
|
| 7 | Основное свойство алгебраической дроби | УИНМ | Основное свойство алгебраической дроби. Правило сокращение дробей. Правило приведение дробей к общему знаменателю. | Знать основное свойство алгебраической дроби Иметь представление о действиях сокращение дробей приведение дроби к общему знаменателю Уметь применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении Преобразовывать алгебраические дроби к дроби с одинаковыми знаменателями раскладывать числитель и знаменатель дроби на простые множители |
|
| 8 | Основное свойство алгебраической дроби | УЗЗ |
|
| 9 | Сложение алгебраических дробей с одинаковыми знаменателями | УИНМ | Алгоритм сложения и вычитания дробей одинаковыми знаменателями
| Иметь представление сложении и вычитании дробей с одинаковыми знаменателями Знать алгоритм сложения и вычитания дробей с одинаковыми знаменателями Уметь складывать и вычитать дроби с одинаковыми знаменателями ,находить общий знаменатель нескольких дробей |
|
| 10 | Вычитание алгебраических дробей с одинаковыми знаменателями | УЗЗ |
|
| 11 | Сложение алгебраических дробей с разными знаменателями | УИНМ | Правило приведения алгебраических дробей к общему знаменателю; алгоритм сложения и вычитания дробей с разными знаменателями.
| Знать понятие наименьший общий знаменатель, дополнительный множитель, правило приведения алгебраических дробей к общему знаменателю, алгоритм сложения и вычитания дробей с разными знаменателями Уметь находить общий знаменатель нескольких дробей, упрощать выражения наиболее рациональным способом |
|
| 12 | Вычитание алгебраических дробей с разными знаменателями | УЗЗ |
|
| 13 | Сложение и вычитание алгебраических дробей с разными знаменателями | УЗЗ |
|
| 14
| Сложение и вычитание алгебраических дробей с разными знаменателями | УЗЗ |
|
| 15 | Контрольная работа № 1 «Сложение и вычитание алгебраических дробей » | УК | Уметь применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении; преобразовывать алгебраические дроби; складывать и вычитать дроби; упрощать выражения наиболее рациональным способом. |
|
| 16 | Умножение и деление алгебраических дробей. | УИНМ | Правило выполнения действий умножения и деления алгебраических дробей.
| Знать правило выполнения действий умножения и деления алгебраических дробей Уметь пользоваться алгоритмами умножения и деления дробей, возведение дроби в степень упрощая выражения |
|
| 17 | Возведение алгебраической дроби в степень | УЗЗ | Правило выполнения возведение дроби в степень.
|
|
| 18 | Действия с алгебраическими дробями | УИНМ | Преобразования рациональных выражений, используя все действия с алгебраическими дробями. | Знать как преобразовывают рациональные выражения используя все действия с алгебраическими дробями Уметь выполнять преобразования рациональных выражений используя все действия с алгебраическими дробями |
|
| 19 | Преобразование рациональных выражений | УЗЗ |
|
| 20 | Первые представления о решении рациональных уравнений | УИНМ | Определение рациональных уравнений, об освобождении от знаменателя при решении уравнений | Знать определение рациональных уравнений, о освобождении от знаменателя при решении уравнений, как решать рациональные уравнения и как составлять математические модели реальных ситуаций Уметь решать рациональные уравнения |
|
| 21 | Первые представления о решении рациональных уравнений | УЗЗ | Рациональные уравнения и как составлять математические модели реальных ситуаций. |
|
| 22 | Степень с отрицательным целым показателем | УИНМ | Определение степени с натуральным показателем, степени с отрицательным показателем, Умножение, деление и возведение в степень степени числа
| Знать определение степени с натуральным показателем, степени с отрицательным показателем, умножение, деление и возведение в степень степени числа Уметь выполнять упрощение выражений со степенями с отрицательным показателем |
|
| 23 | Степень с отрицательным целым показателем | УЗЗ |
|
| 24 | Степень с отрицательным целым показателем | УЗЗ |
|
| 25 | Контрольная работа № 2 «Алгебраические дроби » | УК | Уметь преобразовывать рациональные выражения, используя все действия с алгебраическими дробями |
|
| Раздел 2. Четырехугольники 14 часов |
| 26 | Многоугольники | УИНМ | Многоугольники, выпуклые многоугольники. сумма углов выпуклого многоугольника, элементы многоугольника | Знать определение многоугольника Формулу суммы углов выпуклого многоугольника Уметь распознавать на чертежах многоугольники используя определение Применять формулу суммы углов выпуклого многоугольника при нахождении элементов многоугольника |
|
| 27 | Сумма углов выпуклого многоугольника | УЗЗ |
|
| 28 | Параллелограмм.Свойства параллелограмма. | УИНМ | Определение параллелограмма Свойства параллелограмма Признаки параллелограмма
| Знать определение параллелограмма и его свойства, формулировки признаков Уметь распознавать на чертежах среди четырёхугольников параллелограммы. Доказывать что данный четырёхугольник параллелограмм Выполнять чертежи по условию задачи, находить углы и стороны параллелограмма используя свойство углов и сторон
|
|
| 29 | Параллелограмм. Свойства параллелограмма | УЗЗ |
|
| 30 | Признаки параллелограмма | УИНМ |
|
| 31 | Признаки параллелограмма | УЗЗ |
|
| 32 | Трапеция. Средняя линия трапеции | УИНМ | понятие трапеции, средняя линия трапеции, равнобедренная трапеция и её свойства.
| Знать: определение трапеции, свойства равнобедренной трапеции. Уметь: распознавать трапецию, её элементы, виды на чертежах, находить углы и стороны равнобедренной трапеции, используя её свойства. |
|
| 33 | Трапеция. Решение задач | УИНМ | Теорема Фалеса
Задачи на построения | Знать: формулировку теоремы Фалеса. Уметь: применять теорему Фалеса в процессе решения задач. Знать: основные типы задач на построения. Уметь: делить отрезок на n равных частей, выполнять необходимые построения. |
|
| 34 | Прямоугольник. | УИНМ | Прямоугольник, его элементы, свойства и признаки. | Знать: определение прямоугольника, его элементы, свойства и признаки. Уметь: распознавать на чертежах прямоугольники, находить их стороны и углы, выполнять чертёж по условию задачи; применять признаки при решении задач. |
|
| 35 | Квадрат. | УИНМ | Понятие ромба квадрата их свойства и признаки | Знать определения квадрата ромба их элементы свойства и признаки Уметь распознавать на чертежах рассматриваемые четырехугольники находить их стороны и углы, используя свойства, выполнять чертёж по условию задачи, применять признаки при решении задач, находить стороны квадрата, если известны части сторон, используя свойства прямоугольного треугольника |
|
| 36 | Ромб и квадрат. | УЗЗ |
|
| 37 | Осевая и центральная симметрии | КУ | Осевая и центральная симметрии, как свойства фигур. | Знать: виды симметрии в многоугольниках. Уметь: строить симметричные точки и распознавать фигуры, обладающие симметрией. |
|
| 38 | Решение задач
| УЗЗ | прямоугольник, его элементы, свойства и признаки; понятие ромба, квадрата, их свойства и признаки; осевая и центральная симметрии, как свойства фигур. | Знать: определения прямоугольника, квадрата, ромба, их элементы, свойства и признаки; виды симметрии в многоугольниках. Уметь: распознавать на чертежах рассматриваемые 4-хугольники, находить их стороны и углы, используя свойства; строить симметричные точки и распознавать фигуры, обладающие симметрией; выполнять чертёж по условию задачи; применять признаки при решении задач; находить стороны квадрата, если известны части сторон, используя свойства прямоугольного треугольника. |
|
| 39 | Контрольная работа №3 «Четырёхугольники» | УК | Уметь находить: в прямоугольнике угол между диагоналями. Используя свойство диагоналей, углы в прямоугольной и равнобедренной трапециях, используя свойства трапеции и сторон параллелограмма. |
|
| 40 |
| 40 | Рациональные числа
| УИНМ | Понятие рациональные числа, бесконечная десятичная дробь | Знать понятие рациональные числа бесконечная десятичная дробь |
|
| 41 | Рациональные числа
| УЗЗ | Понятие рациональные числа, бесконечная десятичная дробь |
|
| 42 | Понятие квадратного корня из неотрицательного числа | УИНМ | Понятие квадратного корня из неотрицательного числа.
| Знать понятие квадратного корня из неотрицательного числа Уметь извлекать квадратные корни из неотрицательного числа |
|
| 43 | Понятие квадратного корня из неотрицательного числа | УЗЗ |
|
| 44 | Иррациональные числа
| КУ | Понятие иррационального числа | Знать понятие иррациональное число |
|
| 45 | Множество действительных чисел | КУ | Делимость целых чисел; деление с остатком | Знать о делимости целых чисел; о делении с остатком |
|
| 46 | Функция у =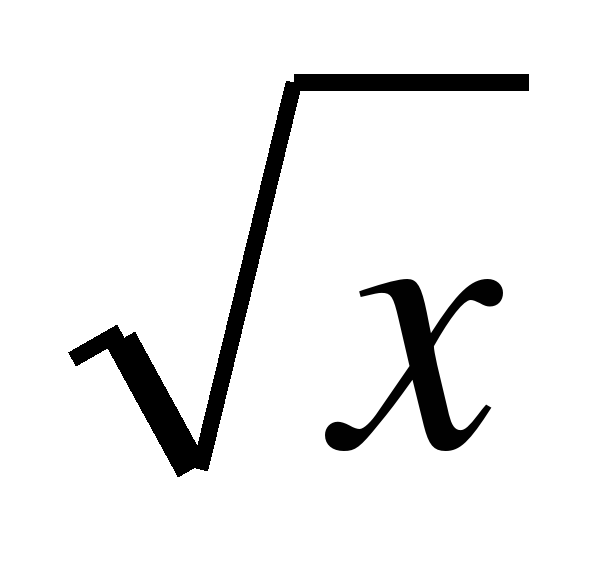 , ее свойства и , ее свойства и график | УИНМ | Функция у =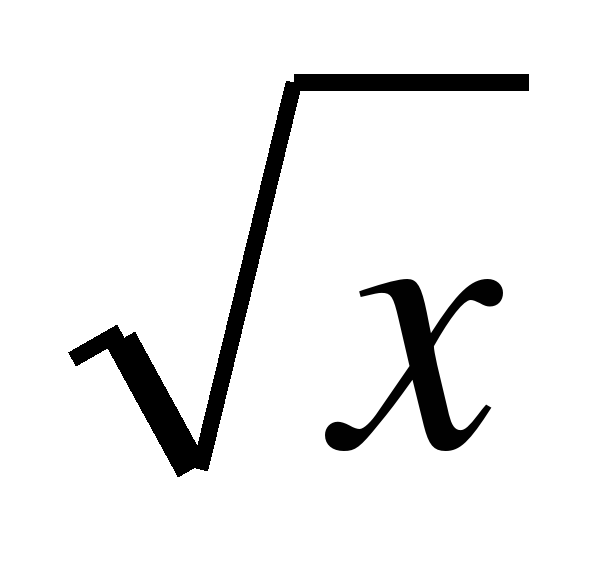 , ее свойства и , ее свойства и график | Знать понятие о функции У=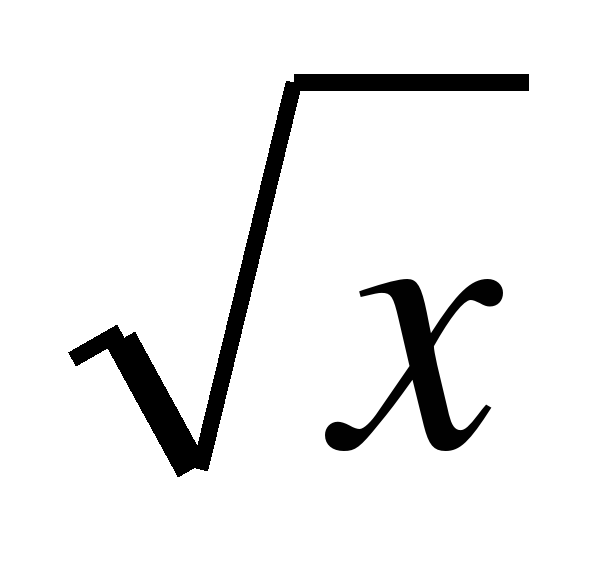 знать её свойства и график знать её свойства и график Уметь строить и читать график функции у=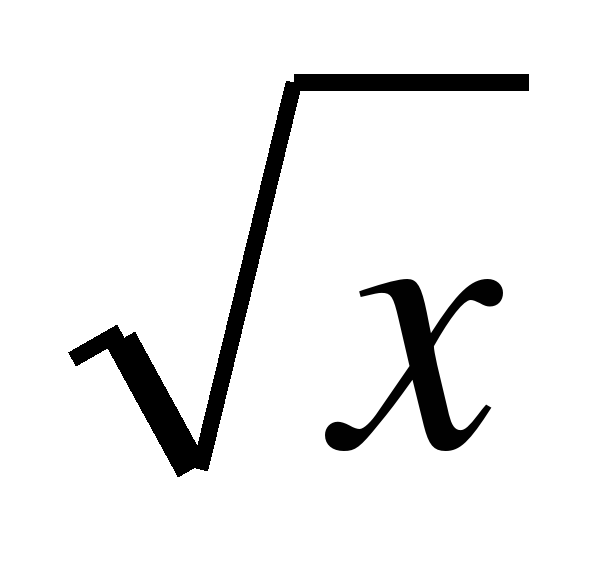
|
|
| 47 | Функция у =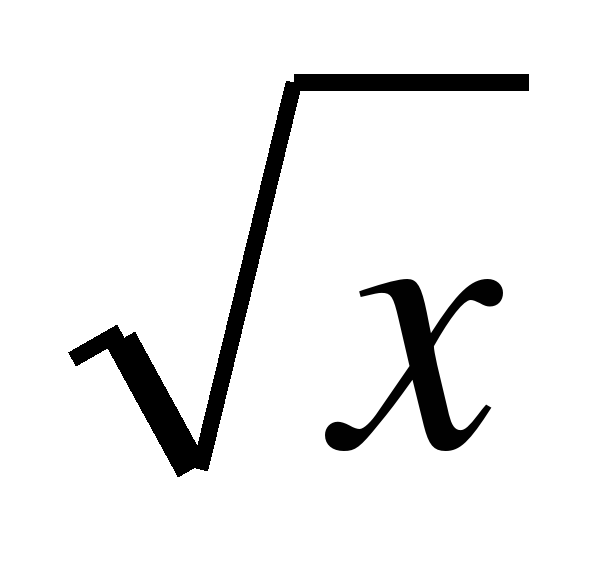 , ее свойства и , ее свойства и график | УЗЗ | Функция у =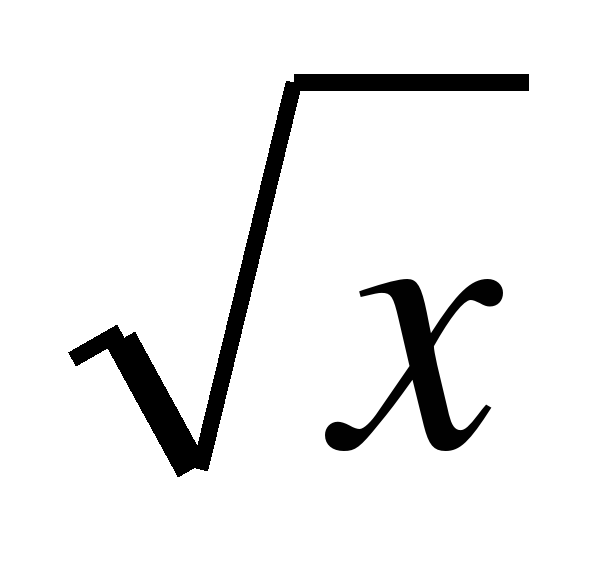 , ее свойства и , ее свойства и график |
|
| 48 | Свойства квадратных корней | УИНМ | Свойства квадратных корней | Знать свойства квадратных корней Уметь применять свойства квадратных корней для упрощения выражений и вычисления корней |
|
| 49 | Применение свойств в вычислениях. | УЗЗ | Свойства квадратных корней |
|
| 50 | Преобразование выражений, содержащих операцию извлечения квадратного корня | УИНМ | Преобразование выражений, содержащих операцию извлечения квадратного корня | Знать о преобразовании выражений об операциях извлечения квадратного корня и освобождение от иррациональности в знаменателе Уметь упрощать выражения с помощью извлечения квадратного корня и освобождение от иррациональности в знаменателе |
|
| 51 | Преобразование выражений, содержащих операцию извлечения квадратного корня | УЗЗ |
|
| 52 | Преобразование выражений, содержащих операцию извлечения квадратного корня | УЗЗ |
|
| 53 | Преобразование выражений, содержащих операцию извлечения квадратного корня | УЗЗ |
|
| 54 | Повторение по теме « Свойства квадратного корня»
| УОСИЗУ | Преобразование выражений, содержащих операцию извлечения квадратного корня |
|
|
|
| 55 | Контрольная работа №4 «Функция 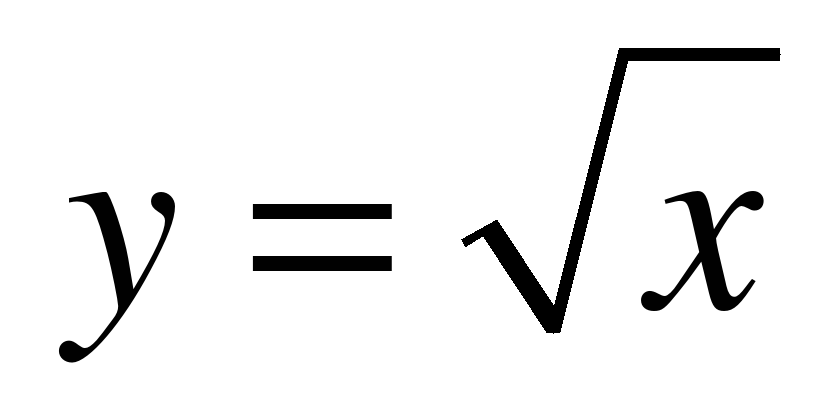 . Свойства квадратного корня » . Свойства квадратного корня » | УК | Уметь строить график функции 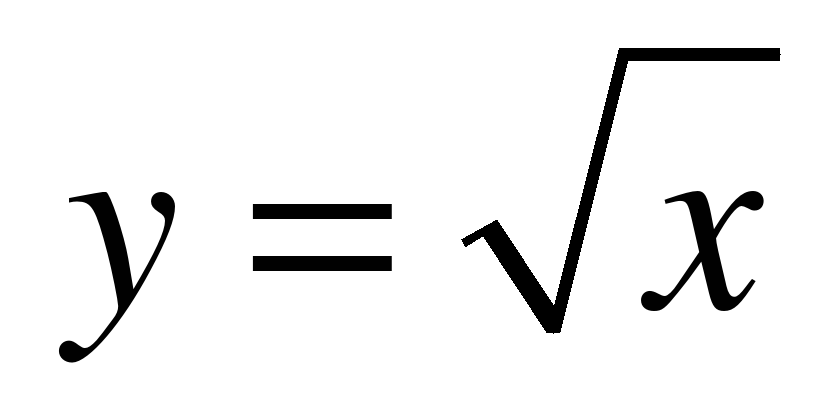 и описывать ее свойства; применять свойства квадратных корней для упрощения выражений и вычисления корней; упрощать выражения, с помощью извлечения квадратного корня и освобождение от иррациональности в знаменателе. и описывать ее свойства; применять свойства квадратных корней для упрощения выражений и вычисления корней; упрощать выражения, с помощью извлечения квадратного корня и освобождение от иррациональности в знаменателе. |
|
| 56 | Модуль действительного числа
| КУ | Определение и свойства модуля действительного числа. | Знать определение модуля действительного числа Уметь применять свойства модуля |
|
| 57 | Модуль действительного числа. График функции модуль.
| УЗЗ | Определение и свойства модуля действительного числа. |
|
| 58 | Модуль действительного числа
| УЗЗ | Определение и свойства модуля действительного числа. |
|
| Раздел 4. Площади фигур 16ч |
| 59 | Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. | КУ | Единицы измерения площадей, площадь прямоугольника, основные свойства площадей | Знать представление о способе измерения площадей многоугольников свойства площадей Формулу площади прямоугольника Уметь вычислять площади квадрата прямоугольника используя формулы |
|
| 60 | Площадь прямоугольника. | УЗЗ |
|
| 61 | Площадь параллелограмма. | УИНМ | Параллелограмм, основание и высота параллелограмма, площадь параллелограмма | Знать формулу площади параллелограмма Уметь вычислять площадь параллелограмма используя формулу Выводить формулу площади параллелограмма Решать задачи на вычисление площадей |
|
| 62 | Площадь параллелограмма. | УЗЗ |
|
| 63 | Площадь треугольника. Формула Герона
| УИНМ | Треугольник, основание и высота, площадь треугольника, соотношение площадей (Формула Герона) | Знать формулу площади треугольника; уметь находить площадь прямоугольного треугольника; находить площадь треугольника в случае, если равны их высоты или угол |
|
| 64 | Площадь треугольника. Формулы, выражающие площадь треугольника: через две стороны и угол между ними | УЗЗ | Площадь треугольника. Формулы, выражающие площадь треугольника: через две стороны и угол между ними | Знать формулу площади треугольника; уметь находить площадь прямоугольного треугольника через две стороны и угол между ними |
|
| 65 | Площадь трапеции | УИНМ | Трапеция, высота трапеции, площадь трапеции | Знать формулу вычисления площади трапеции Уметь доказывать формулу площади трапеции, находить площадь трапеции, используя формулу |
|
| 66 | Площадь трапеции | УЗЗ |
|
| 67 | Решение задач по теме «Площади фигур».
| УЗЗ | Формулы площадей прямоугольника, параллелограмма, треугольника, трапеции | Знать и уметь применять формулы площадей при решении задач |
|
| 68 | Решение задач по теме «Площади фигур»
| УЗЗ | Уметь решать задачи на вычисления площадей |
|
| 69 | Теорема Пифагора.
| УИНМ | Теорема Пифагора. | Знать формулировку теоремы Пифагора. Уметь доказывать теорему Пифагора; решать задачи на нахождение гипотенузы или катета в прямоугольном треугольнике |
|
| 70 | Теорема Пифагора и теорема ей обратная.
| КУ | Теорема Пифагора и теорема ей обратная. | Знать: формулировку теоремы Пифагора и основные этапы её доказательства и формулировку обратной ей теоремы. Уметь: находить стороны треугольника, используя теорему Пифагора; Доказывать обратную теорему и применять её при решении задач.
|
|
| 71 | Решение задач на применение теоремы Пифагора
| УЗЗ | Применение теоремы Пифагора и обратной ей при решении задач | Знать формулировку теоремы Пифагора и формулировку обратной ей теоремы Уметь выполнять чертёж по условию задачи, находить элементы треугольника, используя теорему Пифагора, определять вид треугольника, используя теорему обратную теореме Пифагора |
|
| 72 | Решение задач
| УЗЗ |
|
| 73 | Решение задач
| УОИСЗН | Площадь параллелограмма, треугольника, трапеции, теорема Пифагора | Уметь находить площадь параллелограмма, треугольника, трапеции по формулам; Уметь применять теорему Пифагора при решении задач |
|
| 74 | Контрольная работа №5 «Площади фигур» | УК | Уметь: находить площадь треугольника по известной стороне и высоте, проведённой к ней; находить элементы прямоугольного треугольника, используя теорему Пифагора; площадь и периметр ромба по его диагоналям, используя теорему Пифагора. |
|
| Раздел 5. Квадратичная функция. Функция у = к/х 18 часов |
| 75 | Функция у = kx2, ее свойства и График, парабола | УИНЗ | Функция у = kx2, ее свойства и график Строить графики кусочно заданных функций, Решать графически уравнения и системы уравнений | Знать определение функции вида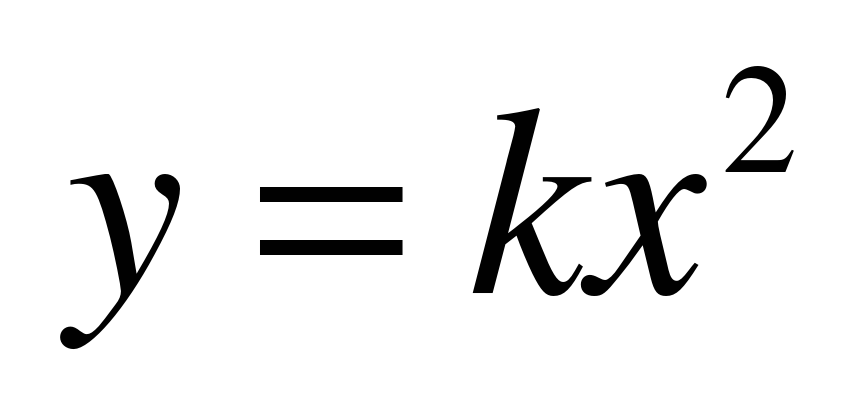 о ее графике и свойствах о ее графике и свойствах Уметь строить график функции строить графики кусочно заданных функций Решать графически уравнения и системы уравнений определять число решений системы уравнений с помощью графического метода |
|
| 76 | Функция у = kx2, ее свойства и график | УЗЗ |
|
| 77 | Функция у = kx2, ее свойства и график | УЗЗ |
|
| 78 | Функция, описывающая обратную пропорциональную зависимости, её график, гипербола. | УИНЗ | Функция у = к/х, ее свойства и График. Строить графики кусочно-заданных функций; решать графически уравнения и системы уравнений. | Знать определение функции вида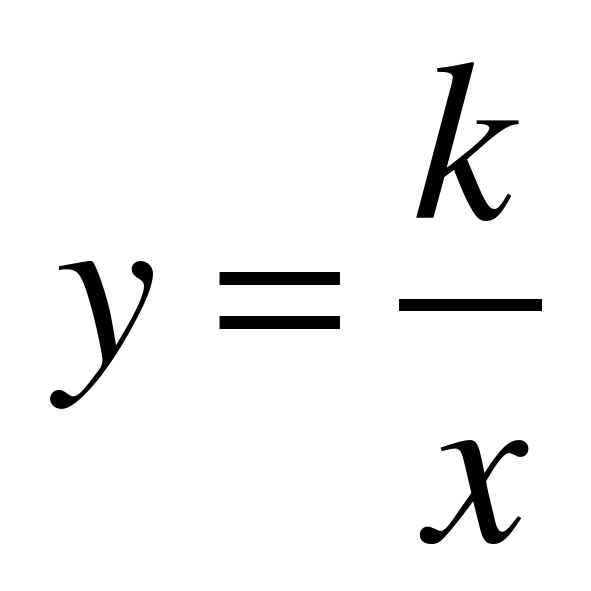 , о ее графике и свойствах , о ее графике и свойствах Уметь строить графикфункции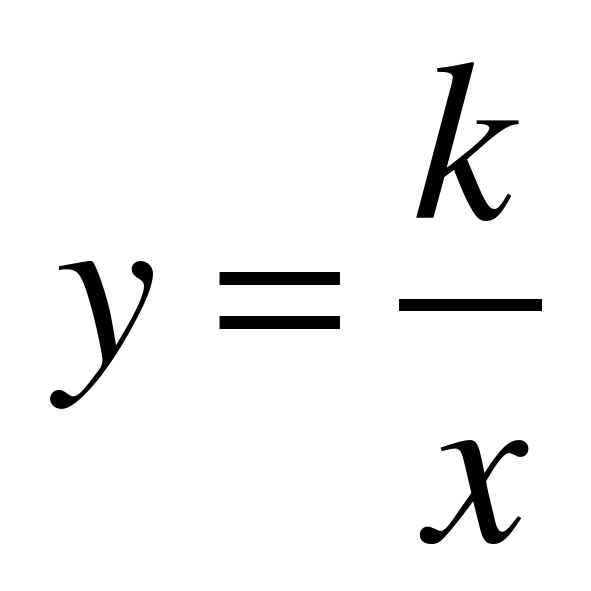 строить графики кусочно заданных функций, решать графически уравнения и системы уравнений, определять число решений системы уравнений с помощью графического метода строить графики кусочно заданных функций, решать графически уравнения и системы уравнений, определять число решений системы уравнений с помощью графического метода |
|
| 79 | Функция, описывающая обратную пропорциональную зависимости, её график, гипербола. | УЗЗ |
|
| 80 | Контрольная работа №6 «Квадратичная функция. Функция 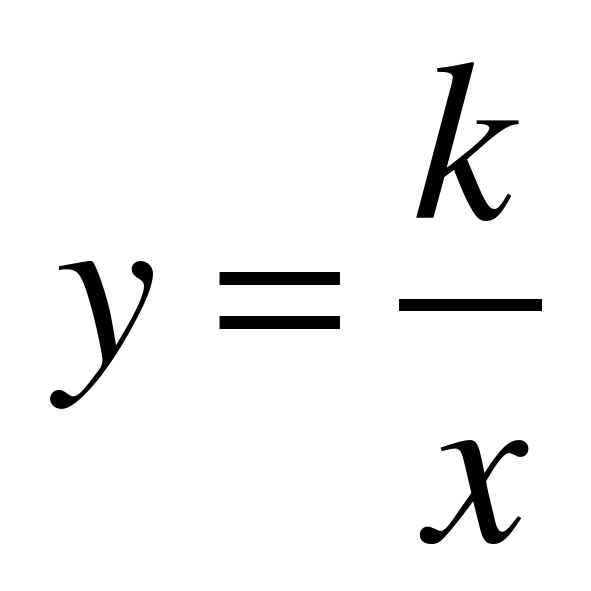 » » | УК | Уметь строить график функции у = kx2 и 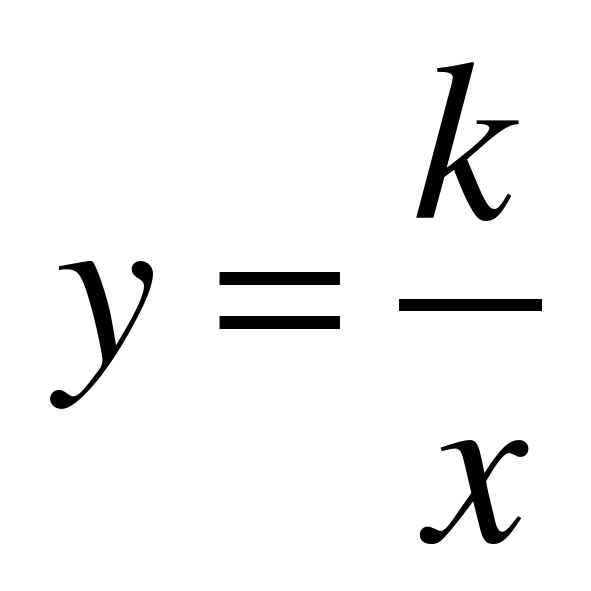 ; строить графики кусочно-заданных функций; решать графически уравнения и системы уравнений, определять число решений системы уравнений с помощью графического метода. ; строить графики кусочно-заданных функций; решать графически уравнения и системы уравнений, определять число решений системы уравнений с помощью графического метода. |
|
| 81 | Как построить график функции у = f(x+l), если известен график функции у = f(x) | УИНЗ | Алгоритм построения графика функции у = f(x+l), если известен график функции у = f(x) | Знать как с помощью параллельного переноса вправо или влево построить график функции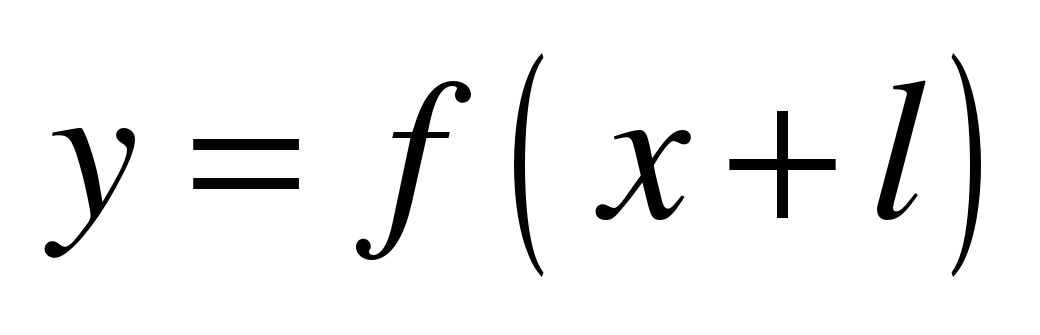 Уметь по алгоритму построить график функции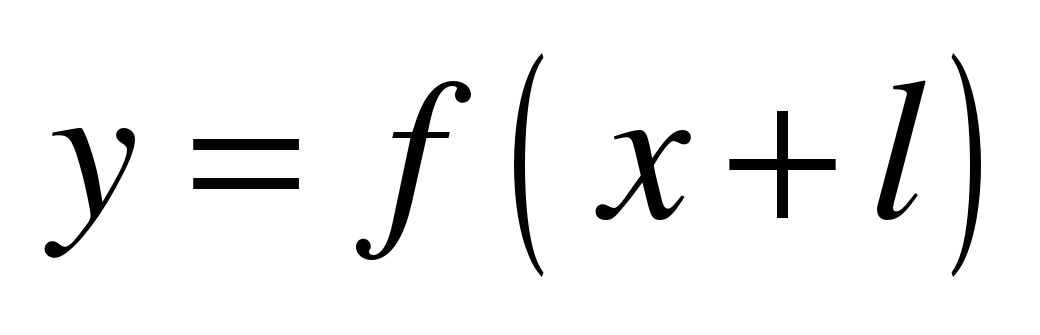 его прочитать и описать свойства его прочитать и описать свойства |
|
| 82 | Как построить график функции у = f(x+l), если известен график функции у = f(x) | УЗЗ |
|
| 83 | Как построить график функции у = f(x) + m, если известен график функции у = f(x) | УИНЗ | Алгоритм построения графика функции у = f(x) + m , если известен график функции у = f(x) | Знать как с помощью параллельного переноса вверх или вниз построить график функции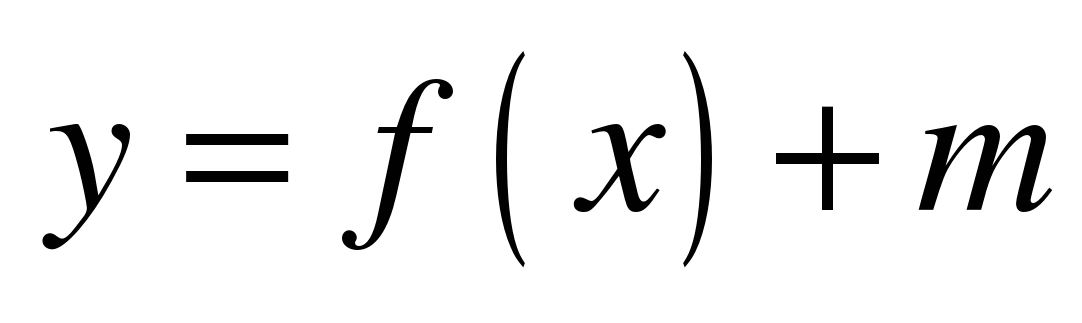 Уметь по алгоритму построить график функции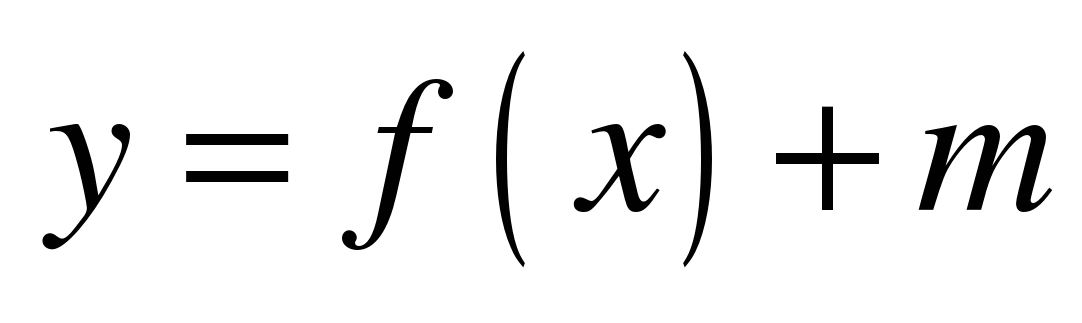 его прочитать и описать свойства его прочитать и описать свойства |
|
| 84 | Как построить график функции у = f(x) + m, если известен график функции у = f(x) | УЗЗ |
|
| 85 | Как построить график функции у = f(x + 1) + m, если известен график функции у = f(x) | УИНЗ | Алгоритм построения графика у = f(x + 1) + m, , если известен график функции у = f(x) | Знать как с помощью параллельного переноса вверх или вниз построить график функции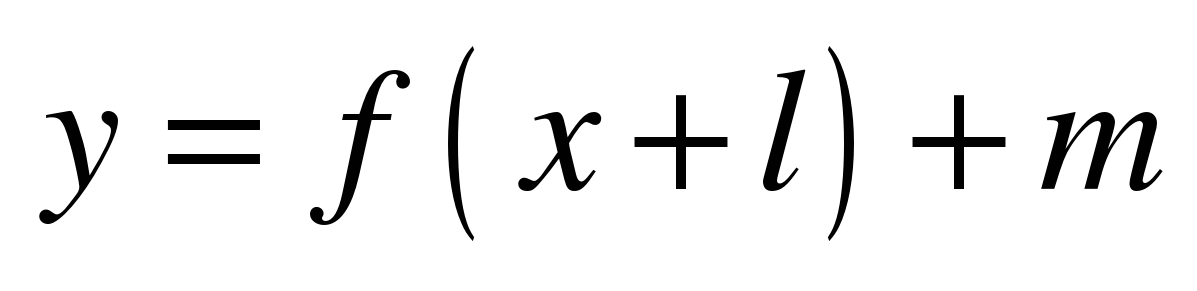 Уметь по алгоритму построить график функции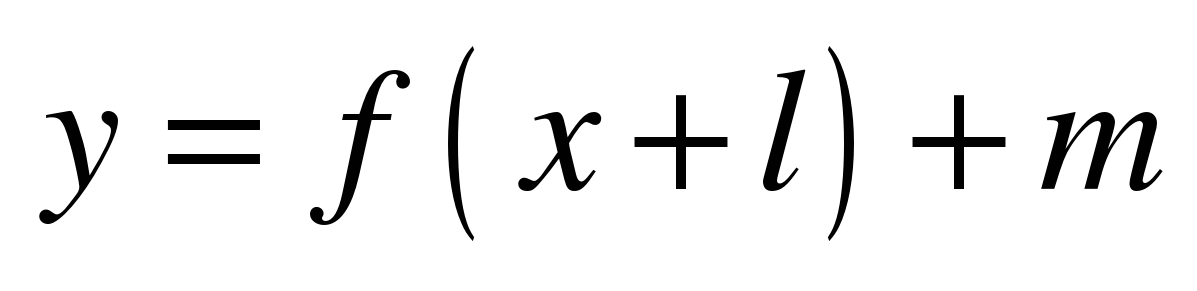 его прочитать и описать свойства его прочитать и описать свойства |
|
| 86 | Параллельный перенос графиков вдоль осей координат и симметрия относительно осей | УЗЗ |
|
| 87 | Функция у = ах2 + bх + с, ее свойства и график | УИНЗ | Алгоритм построения графика функции у = ах2 + bх + с, если известен график функции у = f(x) | Знать иметь представление о функции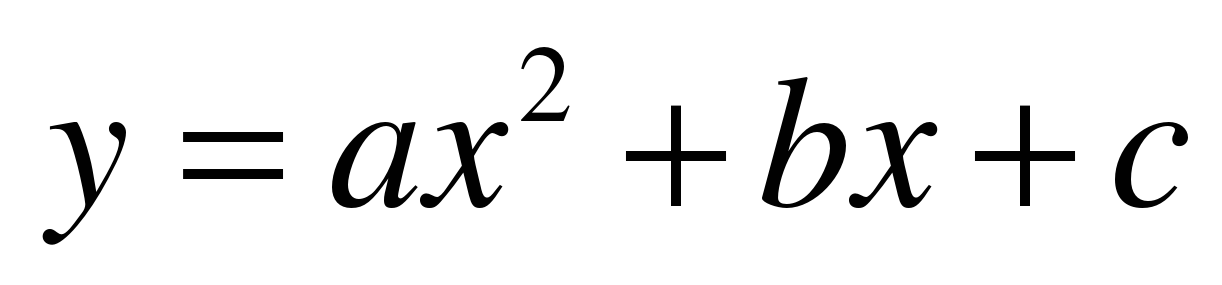 о ее графике и свойствах о ее графике и свойствах Уметь строить график функции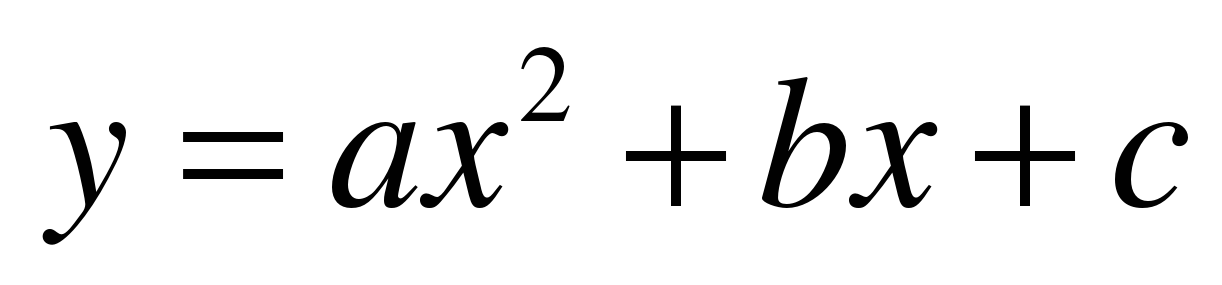 описывать свойства по графику описывать свойства по графику
|
|
| 88 | Функция у = ах2 + bх + с, ее свойства и график. | УЗЗ |
|
| 89 | Функция у = ах2 + bх + с, ее свойства и график | УЗЗ |
|
| 90 | Графическое решение квадратных уравнений | КУ | Графический способ решения квадратных уравнений | Знать способы решения квадратных уравнений. Уметь решать квадратные уравнения графическим способом. |
|
| 91 | Графическое решение квадратных уравнений | КУ | Знать способы решения квадратных уравнений. Уметь решать квадратные уравнения графическим способом. |
|
| 92 | Контрольная работа №7 «Графики функций. Решение уравнений и их систем графическим способом » | УК | Уметь строить графики с помощью параллельного переноса; решать уравнения и системы графическим способом. |
|
| Раздел 6. Подобные треугольники 20ч |
| 93 | Подобие треугольников; коэффициент подобия. | КУ | Подобие треугольников, коэффициент подобия. | Знать: определение пропорциональных отрезков подобных треугольников, свойство биссектрисы треугольника. Уметь: находить элементы треугольника. Используя свойство биссектрисы. |
|
| 94 | Отношение площадей подобных фигур. | УИНМ | Связь между площадями подобных фигур | Знать: формулировку теоремы об отношении площадей подобных треугольников. Уметь: находить отношение площадей, составлять уравнения по условию задачи. |
|
| 95 | Первый признак подобия треугольников
| УИНМ | Первый признак подобия треугольников | Знать формулировку первого признака подобия треугольников и его доказательство Уметь применять при решении задач, выполнять чертёж по условию задачи |
|
| 96 | Первый признак подобия треугольников
| УЗЗ |
|
| 97 | Второй признак подобия треугольников
| УИНЗ | Второй и третий признаки подобия треугольников | Знать формулировки признаков подобия треугольников Уметь доказывать признаки, применять их при решении задач |
|
| 98 | Третий признак подобия треугольников
| УЗЗ |
|
| 99 | Решение задач «Признаки подобия треугольников»
| УОИСЗН | Применение признаков подобия при решении задач | Уметь: доказывать подобия треугольников и находить элементы треугольника, используя признаки подобия. |
|
| 100 | Контрольная работа №8 «Признаки подобия треугольников» | УК | Уметь: находить стороны, углы, отношения сторон, периметров и площадей подобных треугольников, используя признаки подобия; доказывать подобия треугольников, используя наиболее эффективные признаки подобия. |
|
| 101 | Средняя линия треугольника | КУ | Средняя линия треугольника | Знать: формулировку о средней линии треугольника. Уметь проводить доказательство теоремы о средней линии треугольника и находить её. |
|
| 102 | Свойство медианы треугольника
| УИНЗ | Свойство медианы треугольника | Знать: формулировку свойства медианы треугольника; Уметь: находить элементы треугольника, используя свойство медианы. |
|
| 103 | Пропорциональные отрезки
| УИНЗ | Среднее пропорциональное | Знать: понятие среднего пропорционального, Свойство высоты, проведённой из вершины прямого угла треугольника; Уметь: находить элементы прямоугольного треугольника, используя свойство высоты. |
|
| 104 | Пропорциональные отрезки в прямоугольном треугольнике | УЗЗ | Пропорциональные отрезки в прямоугольном треугольнике | Знать: теоремы о пропорциональности отрезков в прямоугольном треугольнике. Уметь: использовать теоремы при решении задач. |
|
| 105 | Связь между площадями подобных фигур. Измерительные работы на местности | КУ | Применение подобия треугольников в измерительных работах на местности | Знать: как находить расстояние до недоступной точки. Уметь: использовать подобие треугольников в измерительных работах на местности, описывать реальные ситуации на языке геометрии. |
|
| 106 | Задачи на построение
| КУ | Задачи на построение | Знать: знать этапы построений. Уметь: строить биссектрису, высоту, медиану треугольника, угол, равный данному, прямую, параллельную данной. |
|
| 107 | Задачи на построение методом подобных треугольников | УЗЗ | Метод подобия | Знать: метод подобия. Уметь: применять метод подобия при решении задач на построение |
|
| 108 | Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
| УИНЗ | Понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника; основное тригонометрическое тождество | Знать: понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника; основное тригонометрическое тождество. Уметь: находить значение одной из тригонометрических функций по значению другой. |
|
| 109 | Значения синуса, косинуса, тангенса для углов 30ْ, 45ْ, 60ْ, 90ْ
| КУ | Значения синуса, косинуса, тангенса для углов 30ْ, 45ْ, 60ْ, 90.ْ | Знать: значения синуса, косинуса, тангенса для углов 30ْ, 45ْ, 60ْ, 90.ْ Уметь определять значения синуса, косинуса, тангенса по заданному значению углов. |
|
| 110 | Соотношения между сторонами и углами прямоугольного треугольника
| УИНЗ | Решение прямоугольных треугольников | Знать: соотношения между сторонами и углами прямоугольного треугольника; Уметь: решать прямоугольные треугольники, используя понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника |
|
| 111 | Решение задач на применение подобия треугольников
| УЗЗ | Задачи на применение подобия треугольников и соотношения между сторонами и углами прям-го треугольника | Знать: теорию подобия треугольников и соотношения между сторонами и углами прям-го треугольника. Уметь: выполнять чертёж по условию задачи, решать задачи с использованием тригонометрии.
|
|
| 112 | Контрольная работа №9 «Подобие треугольников и соотношение между сторонами и углами прямоугольного треугольника» | УК | средняя линия треугольника; свойство медиан; соотношения между сторонами и углами прямоугольного треугольника | Уметь: находить стороны треугольника по отношению средних линий и периметру, а также используя свойство точки пересечения медиан, Решать прямоугольный треугольник, используя соотношения между сторонами и углами.
|
|
| Раздел 7. Квадратные уравнения 21 ч |
| 113 | Квадратное уравнение: основные понятия | УИНМ | Полное и неполное квадратные уравнении решения неполных квадратных уравнений | Иметь представление о полном и неполном квадратном уравнении о решении неполных квадратных уравнений Уметь решать неполное квадратное уравнение |
|
| 114 | Неполные квадратные уравнения
| УЗЗ |
|
| 115 | Формула корней квадратного уравнения
| УИНМ | Формулы корней квадратного уравнения дискриминанта алгоритм решения квадратного уравнения
| Знать формулы корней квадратного уравнения дискриминанта алгоритм решения квадратного уравнения Уметь используя дискриминант решать квадратные уравнения по алгоритму решать задачи на составление квадратных уравнений |
|
| 116 | Формула корней квадратного уравнения
| УЗЗ |
|
| 117 | Формула корней квадратного уравнения
| УЗЗ |
|
| 118 | Рациональные уравнения
| УИНМ | Алгоритм решения рациональных уравнений используя метод введения новой переменной решать уравнения
| Знать алгоритм решения рациональных уравнений, используя метод введения новой переменной, Уметь решать рациональные уравнения, используя метод введения новой переменной, биквадратные уравнения, уравнения с применением нескольких способов упрощения выражений, входящих в уравнение |
|
| 119 | Решение рациональных уравнений. | УЗЗ |
|
| 120 | Решение рациональных уравнений. | УЗЗ |
|
| 121 | Контрольная работа №10 «Квадратные уравнения» | УК | Уметь решать неполное квадратное уравнение; используя дискриминант, решать квадратные уравнения по алгоритму; решать задачи на составление квадратных уравнений; решать рациональные уравнения, используя метод введения новой переменной; биквадратные уравнения; уравнения с применением нескольких способов упрощения выражений входящих в уравнение. |
|
| 122 | Рациональные уравнения как математические модели реальных ситуаций | УИНМ | Рациональные уравнения как математические модели реальных ситуаций | Уметь решать задачи на числа на движение по дороге на движение по воде выделяя основные этапы математического моделирования |
|
| 123 | Решение текстовых задач алгебраическим способом | УЗЗ |
|
| 124 | Решение текстовых задач алгебраическим способом | УЗЗ |
|
| 125 | Решение текстовых задач алгебраическим способом | УЗЗ |
|
| 126 | Еще одна формула корней квадратного уравнения | УИНМ | Еще одна формула корней квадратного уравнения | Знать алгоритм вычисления корней квадратного уравнения с четным вторым коэффициентом, используя дискриминант Уметь решать квадратные уравнения с четным вторым коэффициентом по формулам корней квадратного уравнения с четным вторым коэффициентом через дискриминант |
|
| 127 | Еще одна формула корней квадратного уравнения | УЗЗ |
|
| 128 | Теорема Виета | УИНМ | Теорема Виета и теорема обратная ей | Знать теорему Виета и обратную теорему Виета Уметь применять теорему Виета и обратную теорему Виета, решая квадратные уравнения, составлять квадратные уравнения по его корням |
|
| 129 | Теорема Виета. Разложение квадратного трехчлена на линейные множители | УЗЗ |
|
| 130 | Контрольная работа №11 «Квадратные уравнения» | УК | Уметь решать задачи на числа, на движение по дороге, на движение по воде, выделяя основные этапы математического моделирования; применять теорему Виета и об обратную теорему Виета, решая квадратные уравнения. |
|
| 131 | Иррациональные уравнения
| УИНМ | Понятие иррационального уравнения, Его решение методом возведения обеих частей в квадрат | Знать понятия иррациональных уравнениях, о равносильных уравнениях, о равносильных преобразованиях уравнений, о неравносильных преобразованиях уравнения, методы возведения в квадрат обеих частей уравнения Уметь решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований |
|
| 132 | Иррациональные уравнения
| УЗЗ |
|
| 133 | Иррациональные уравнения
| УЗЗ |
|
| Раздел 8. Окружность 17ч |
| 134 | Взаимное расположение прямой и окружности, двух окружностей. | КУ | Взаимное расположение прямой и окружности. | Знать: случаи взаимного расположение прямой и окружности. Уметь: определять взаимное расположение прямой и окружности и выполнять чертёж по условию задачи. |
|
| 135 | Касательная и секущая к окружности, равенство касательных, проведенных из одной точки. | УИНМ | касательная и секущая к окружности, точка касания | Знать: понятия касательной, секущей, точек касания, свойство касательной и её признак.
Уметь: доказывать теорему о свойстве касательной ей обратную, проводить касательную к окружности. |
|
| 136 | Решение задач по теме «Окружность». Метрические соотношения в окружности: свойства секущих и касательных.
| УЗЗ | касательная и секущая к окружности, равенство отрезков касательных, проведённых из одной точки, свойство касательной и её признак. | Знать: взаимное расположение прямой и окружности; формулировку свойства касательной о её перпендикулярности радиусу, формулировку свойства отрезков касательных, проведённых из одной точки. Уметь: находить радиус, проведённый в точку касания, по касательной и наоборот. |
|
| 137 | Центральный угол. Центральный, вписанный угол.
| КУ | центральные и вписанные углы, градусная мера длины дуги окружности. | Знать: понятие градусной меры дуги, центрального угла. Уметь: решать простейшие задачи на вычисление градусной меры дуги. |
|
| 138 | Величина вписанного угла.
| КУ | понятие вписанного угла, теорема о вписанном угле и следствие из неё | Знать: определение вписанного угла, теорему о вписанном угле и следствие из неё. Уметь: распознавать на чертежах вписанные углы, находить величину вписанного угла. |
|
| 139 | Теорема об отрезках пересекающихся хорд. | КУ | Теорема об отрезках пересекающихся хорд | Знать: формулировку теоремы, Уметь: доказывать и применять теорему при решении задач, выполнять чертёж по условию задачи. |
|
| 140 | Решение задач по теме «центральные и вписанные углы»
| УЗЗ | центральные и вписанные углы,
| Знать: формулировки определений вписанного и центрального углов, теорему об отрезках пересекающихся хорд. Уметь: находить величину вписанного и центрального углов. |
|
| 141 | Свойство биссектрисы
| КУ | Теорема о свойстве биссектрисы угла | Знать: формулировку теоремы о свойстве равноудалённости каждой точки биссектрисы угла и этапы её доказательства. Уметь: находить элементы треугольника, используя свойство биссектрисы, выполнять чертёж по условию задачи |
|
| 142 | Серединный перпендикуляр. Свойство серединного перпендикуляра к отрезку. | КУ | понятие серединного перпендикуляра, теорема о серединном перпендикуляре. | Знать: понятие серединного перпендикуляра, формулировку теоремы о нём. Уметь: доказывать и применять теорему для решения задач на нахождение элементов треугольника. |
|
| 143 | Замечательные точки треугольника
| КУ | Теорема о точке пересечения высот треугольника, четыре замечательные точки треугольника | Знать: четыре замечательные точки треугольника, формулировку теоремы о пересечении высот треугольника. Уметь: находить элементы треугольника
|
|
| 144 | Окружность, вписанная в треугольник
| КУ | понятие вписанной окружности. теорема об окружности, вписанной в треугольник | Знать: понятие вписанной окружности, теорему об окружности, вписанной в треугольник. Уметь: распознавать на чертежах вписанные окружности, находить элементы треугольника, используя свойства вписанной окружности. |
|
| 145 | Описанные четырехугольники. Свойство описанного четырёхугольника
| КУ | Теорема о свойстве описанного четырёхугольника | Знать: теорему о свойстве описанного четырёхугольника и этапы её доказательства. Уметь: применять свойство описанного 4-хугольника при решении задач, выполнять чертёж по условию задачи |
|
| 146 | Описанная окружность. Окружность, описанная около треугольника
| КУ | описанная окружность, теорема об описанной окружности около треугольника | Знать: определение описанной окружности, формулировку теоремы об окружности, описанной около треугольника. Уметь: доказывать теорему и применять её при решении задач, различать на чертежах описанные окружности. |
|
| 147 | Вписанные четырехугольники. Свойство вписанного четырёхугольника | УЗЗ | Свойство углов вписанного четырёхугольника | Знать: формулировку теоремы о вписанном четырёхугольнике, Уметь: выполнять чертёж по условию задачи, опираясь на указанное свойство |
|
| 148 | Решение задач по теме «Окружность»
| УЗЗ | Вписанная и описанная окружности, вписанные и описанные 4-хугольники | Знать: формулировки определений и свойств; Уметь: находить один из отрезков касательных, проведённых из одной точки по заданному радиусу окружности; центральные и вписанные углы по отношению дуг окружностей; отрезки, пересекающихся хорд окружности. Используя теорему о произведении отрезков пересекающихся хорд. |
|
| 149 | Решение задач по теме «Окружность»
| УОИСЗН | Вписанные и центральные углы; вписанная и описанная окружности | Уметь: распознавать на чертежах вписанные и центральные углы, находить их величину; находить один из отрезков касательных, проведённых из одной точки по заданному радиусу окружности; центральные и вписанные углы по отношению дуг окружностей; отрезки, пересекающихся хорд окружности. Используя теорему о произведении отрезков пересекающихся хорд.. Взаимопроверка |
|
| 150 | Контрольная работа №12 «Окружность» | УК | Уметь: находить один из отрезков касательных, проведённых из одной точки по заданному радиусу окружности; центральные и вписанные углы по отношению дуг окружностей; отрезки, пересекающихся хорд окружности. Используя теорему о произведении отрезков пересекающихся хорд. Карточки |
|
| Раздел 9. Неравенства 15ч |
| 151 | Числовые неравенства и их свойства | УИНМ | Свойства числовых неравенств | Знать свойства числовых неравенств Уметь применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств |
|
| 152 | Свойства числовых неравенств. | УЗЗ |
|
| 153 | Свойства числовых неравенств. | УЗЗ |
|
| 154 | График функции, возрастание и убывание функции, промежутки знакопостоянства | УИНМ | Понятие возрастающей убывающей монотонной функции на промежутке Построение и исследование графиков различных функций | Знать понятие возрастающей убывающей монотонной функции на промежутке Уметь построить и исследовать н а монотонность функции линейную квадратную обратной пропорциональности функцию корень
|
|
| 155 | Исследование функций на монотонность | УЗЗ |
|
| 156 | Исследование функций на монотонность | УЗЗ |
|
| 157 | Решение линейных неравенств. | УИНМ | Решение линейных неравенств | Знать о неравенстве с переменной о системе линейных неравенств пересечение решений неравенств системы Уметь изобразить на координатной плоскости точки, координаты которых удовлетворяют неравенству решать неравенства с переменной и системы неравенств с переменной |
|
| 158 | Линейные неравенства с одной переменной и их системы. | УЗЗ | Решение линейных неравенств |
|
| 159 | Квадратные неравенства и их решение | УИНЗ | Решение квадратных неравенств | Знать понятие квадратного неравенства о знаке объединения множества алгоритм решения квадратного неравенства методе интервалов Уметь решать квадратные неравенства по алгоритму и методом интервалов |
|
| 160 | Решение квадратных неравенств | УЗЗ |
|
| 161 | Решение квадратных неравенств | УЗЗ |
|
| 162 | Контрольная работа №13 «Неравенства» | УК | Уметь изобразить на координатной плоскости точки, координаты которых удовлетворяют неравенству; - решать неравенства с переменной и системы неравенств с переменной; решать квадратные неравенства по алгоритму и методом интервалов. |
|
| 163 | Приближенные значения действительных чисел | КУ | Приближенные значения Действительных чисел по недостатку по избытку, округлении чисел погрешности приближения, абсолютной и относительной погрешностях | Знать о приближенном значение по недостатку по избытку округлении чисел погрешности приближения абсолютной и относительной погрешностях Уметь использовать знания о приближенном значение по недостатку по избытку округлении чисел погрешности приближения абсолютной и относительной погрешностях при решении задач |
|
| 164 | Приближенные значения действительных чисел
| УЗЗ |
|
| 165 | Стандартный вид положительного числа
| УИНЗ | Стандартный вид положительного числа | Знать о стандартном виде положительного числа, о порядке числа, о записи числа в стандартной форме. Уметь записывать числа в стандартном виде. |
|
| Раздел 9. Повторение 10 ч |
| 166 | Четырёхугольники и их площади | УОИСЗУ | Формулы площадей прямоугольника квадрата параллелограмма треугольника трапеции | Уметь решать задачи на вычисление площадей |
|
| 167 | Решение задач «Признаки подобия треугольников» | УОИСЗН | Применение признаков подобия при решении задач | Уметь доказывать подобия треугольников и находить элементы треугольника используя признаки подобия |
|
| 168 | Решение задач по теме «Окружность» | УОИСЗУ | Вписанные и центральные углы; вписанная и описанная окружности | Уметь: распознавать на чертежах вписанные и центральные углы, находить их величину; находить один из отрезков касательных, проведённых из одной точки по заданному радиусу окружности; центральные и вписанные углы по отношению дуг окружностей; отрезки, пересекающихся хорд окружности. Используя теорему о произведении отрезков пересекающихся хорд.. |
|
| 169 | Преобразование рациональных выражений | УОИСЗУ | преобразования рациональных выражений, используя все действия с алгебраическими дробями. | Уметь выполнять преобразования рациональных выражений, используя все действия с алгебраическими дробями. |
|
| 170 | Преобразование выражений, содержащих операцию извлечения квадратного корня | УОИСЗУ | Преобразование выражений, содержащих операцию извлечения квадратного корня | Уметь упрощать выражения, с помощью извлечения квадратного корня и освобождение от иррациональности в знаменателе. |
|
| 171 | Квадратные уравнения | УОИСЗУ | Решение квадратных уравнений | Уметь решать неполное квадратное уравнение, используя дискриминант решать квадратные уравнения по алгоритму, решать задачи на составление квадратных уравнений. решать рациональные уравнения, используя метод введения новой переменной. биквадратные уравнения, уравнения с применением нескольких способов упрощения выражений, входящих в уравнение |
|
| 172 | Решение квадратных неравенств | УОИСЗУ | Решение квадратных неравенств | Уметь решать квадратные неравенства по алгоритму и методом интервалов
|
|
| 173 | Контрольная работа №14 «Итоговая контрольная работа» | УК | Проверить умение обобщения и систематизации знаний по основным темам курса математики 8 класса. Уметь проводить самооценку собственных действий |
|
| 174 | Анализ контрольной работы | УОИСЗУ |
|
|
|
| 175 | Заключительный урок |
|
|
|
|
Контрольно-измерительные материалы.
| № | Темы программы | Вид контроля | К/Р |
| 1. | Повторение курса математики 7 класса | Входной тестовый контроль | Входной тест |
| 2. | Алгебраические дроби | Тематический контроль | Контрольная работа №1 Контрольная работа №2 |
| 3. | Четырехугольники | Тематический контроль | Контрольная работа №3 |
| 4. | Функция y=√x. Свойства квадратного корня | Тематический контроль | Контрольная работа №4
|
| 5. | Площади фигур | Тематический контроль | Контрольная работа №5 |
| 6. | Квадратичная функция. Функция у = к/х | Тематический контроль | Контрольная работа №6 Контрольная работа №7 |
| 7. | Подобные треугольники | Тематический контроль | Контрольная работа №8 Контрольная работа №9 |
| 8. | Квадратные уравнения | Тематический контроль | Контрольная работа №10 Контрольная работа №11 |
| 9. | Окружность | Тематический контроль | Контрольная работа №12
|
| 10 | Неравенства | Тематический контроль | Контрольная работа №13
|
| 11 | Итоговое повторение курса 8 класса | Тематический контроль | Итоговая контрольная работа |
|
|
|
Календарно-тематическое планирование
| № п/п | Тема |
|
| Дата |
| 1 | Повторение. Буквенные выражения. |
|
| 2 | Повторение. Параллельные прямые, признаки равенства треугольников. |
|
| 3 | Повторение. Линейная функция. | |
| 4 | Повторение. Свойства прямоугольного треугольника. | |
| 5 | Входная контрольная работа. | |
| 6 | Основные понятия алгебраической дроби. | |
| 7 | Многоугольники. |
|
| 8 | Основное свойство алгебраической дроби. | |
| 9 | Сумма углов выпуклого многоугольника. |
|
| 10 | Основное свойство алгебраической дроби. | |
| 11 | Сложение алгебраических дробей с одинаковыми знаменателями | |
| 12 | Параллелограмм. Свойства параллелограмма. |
|
| 13 | Вычитание алгебраических дробей с одинаковыми знаменателями | |
| 14 | Параллелограмм. Свойства параллелограмма |
|
| 15 | Сложение алгебраических дробей с разными знаменателями | |
| 16 | Вычитание алгебраических дробей с разными знаменателями |
|
| 17 | Признаки параллелограмма |
|
| 18 | Сложение и вычитание дробей с разными знаменателями | |
| 19 | Признаки параллелограмма |
|
| 20 | Сложение и вычитание дробей с разными знаменателями |
|
| 21 | Контрольная работа № 1 «Сложение и вычитание алгебраических дробей » | |
| 22 | Трапеция. Средняя линия трапеции |
|
| 23 | Умножение и деление алгебраических дробей. | |
| 24 | Трапеция. Решение задач |
|
| 25 | Возведение алгебраической дроби в степень | |
| 26 | Действия с алгебраическими дробями | |
| 27 | Прямоугольник. |
|
| 28 | Преобразование рациональных выражений |
|
| 29 | Квадрат. |
|
| 30 | Первые представления о решении рациональных уравнений |
|
| 31 | Первые представления о решении рациональных уравнений |
|
| 32 | Ромб и квадрат. |
|
| 33 | Степень с отрицательным целым показателем |
|
| 34 | Осевая и центральная симметрии |
|
| 35 | Степень с отрицательным целым показателем |
|
| 36 | Степень с отрицательным целым показателем | |
| 37 | Решение задач по теме «Четырехугольники» |
|
| 38 | Контрольная работа № 2 «Алгебраические дроби » | |
| 39 | Контрольная работа №3 «Четырёхугольники» | |
| 40 | Рациональные числа | |
| 41 | Рациональные числа | |
| 42 | Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. | |
| 43 | Понятие квадратного корня из неотрицательного числа | |
| 44 | Площадь прямоугольника. | |
| 45 | Понятие квадратного корня из неотрицательного числа | |
| 46 | Иррациональные числа | |
| 47 | Площадь параллелограмма. | |
| 48 | Множество действительных чисел | |
| 49 | Площадь параллелограмма. | |
| 50 | Функция у =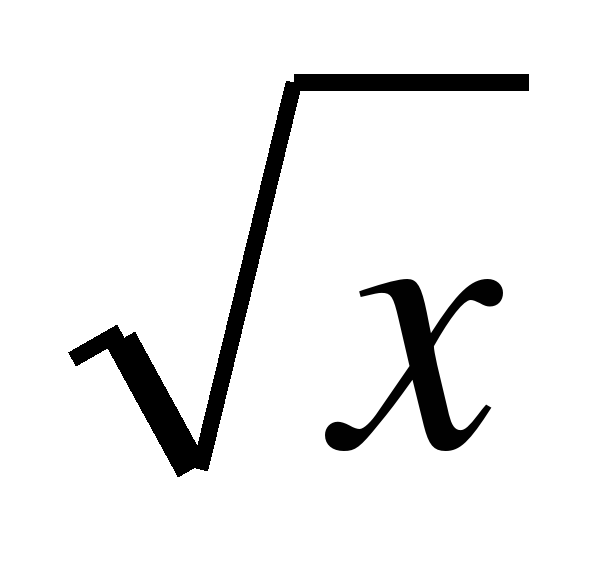 , ее свойства и график , ее свойства и график | |
| 51 | Функция у =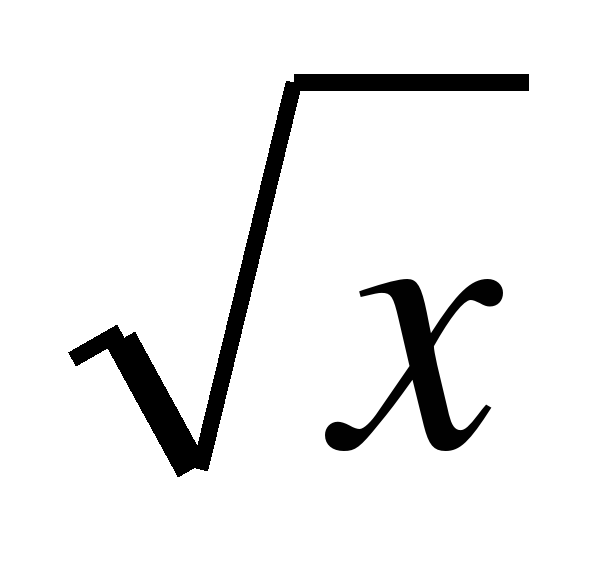 , ее свойства и график , ее свойства и график | |
| 52 | Площадь треугольника. Формула Герона |
|
| 53 | Свойства квадратных корней | |
| 54 | Площадь треугольника. Формулы, выражающие площадь треугольника: через две стороны и угол между ними |
|
| 55 | Применение свойств в вычислениях. | |
| 56 | Преобразование выражений, содержащих операцию извлечения квадратного корня | |
| 57 | Площадь трапеции |
|
| 58 | Преобразование выражений, содержащих операцию извлечения квадратного корня | |
| 59 | Площадь трапеции |
|
| 60 | Преобразование выражений, содержащих операцию извлечения квадратного корня | |
| 61 | Преобразование выражений, содержащих операцию извлечения квадратного корня | |
| 62 | Решение задач по теме «Площади фигур». |
|
| 63 | Повторение по теме « Свойства квадратного корня» | |
| 64 | Решение задач по теме «Площади фигур» |
|
| 65 | Контрольная работа №4 «Функция 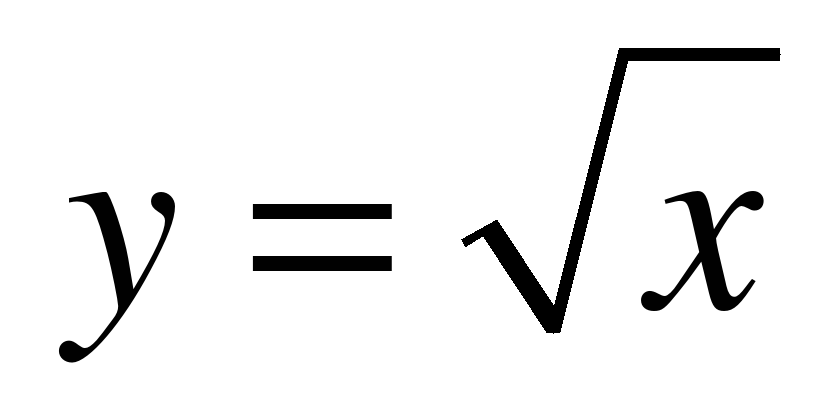 . Свойства квадратного корня» . Свойства квадратного корня» | |
| 66 | Модуль действительного числа | |
| 67 | Теорема Пифагора. |
|
| 68 | Модуль действительного числа. График функции модуль. | |
| 69 | Теорема Пифагора и теорема ей обратная. |
|
| 70 | Модуль действительного числа | |
| 71 | Функция у = kx2, ее свойства и график, парабола | |
| 72 | Решение задач на применение теоремы Пифагора | |
| 73 | Функция у = kx2, ее свойства и график | |
| 74 | Решение задач на применение теоремы Пифагора | |
| 75 | Функция у = kx2, ее свойства и график | |
| 76 | Функция, описывающая обратную пропорциональную зависимости, её график, гипербола. | |
| 77 | Решение задач на применение обратной теоремы Пифагора | |
| 78 | Функция, описывающая обратную пропорциональную зависимости, её график, гипербола. | |
| 79 | Контрольная работа №5 «Площади фигур» | |
| 80 | Контрольная работа №6 «Квадратичная функция. Функция 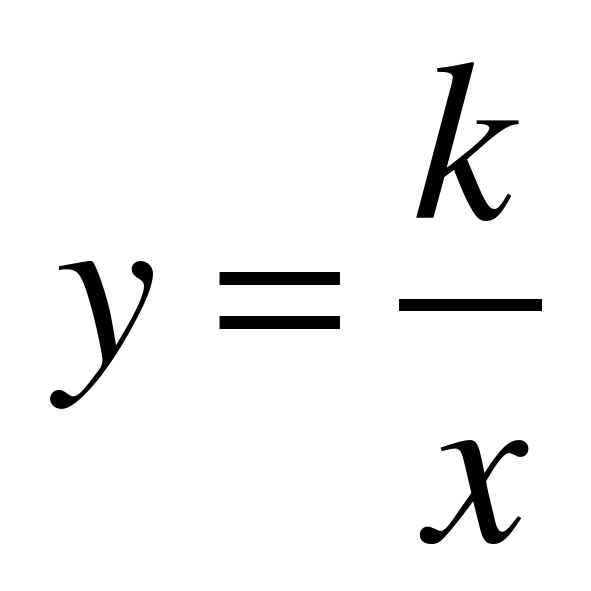 » » | |
| 81 | Как построить график функции у = f(x+l), если известен график функции у = f(x) |
|
| 82 | Подобие треугольников; коэффициент подобия. | |
| 83 | Как построить график функции у = f(x+l), если известен график функции у = f(x) | |
| 84 | Отношение площадей подобных фигур. | |
| 85 | Как построить график функции у = f(x) + m, если известен график функции у = f(x) | |
| 86 | Как построить график функции у = f(x) + m, если известен график функции у = f(x) | |
| 87 | Первый признак подобия треугольников | |
| 88 | Как построить график функции у = f(x + 1) + m, если известен график функции у = f(x) | |
| 89 | Первый признак подобия треугольников | |
| 90 | Параллельный перенос графиков вдоль осей координат и симметрия относительно осей | |
| 91 | Второй признак подобия треугольников | |
| 92 | Функция у = ах2 + bх + с, ее свойства и график | |
| 93 | Функция у = ах2 + bх + с, ее свойства и график. | |
| 94 | Третий признак подобия треугольников | |
| 95 | Функция у = ах2 + bх + с, ее свойства и график | |
| 96 | Решение задач «Признаки подобия треугольников» | |
| 97 | Графическое решение квадратных уравнений |
|
| 98 | Графическое решение квадратных уравнений | |
| 99 | Контрольная работа №8 «Признаки подобия треугольников» | |
| 100 | Контрольная работа №7 «Графики функций. Решение уравнений и их систем графическим способом » | |
| 101 | Средняя линия треугольника | |
| 102 | Квадратное уравнение: основные понятия | |
| 103 | Неполные квадратные уравнения | |
| 104 | Свойство медианы треугольника | |
| 105 | Формула корней квадратного уравнения | |
| 106 | Пропорциональные отрезки | |
| 107 | Формула корней квадратного уравнения | |
| 108 | Формула корней квадратного уравнения |
|
| 109 | Пропорциональные отрезки в прямоугольном треугольнике | |
| 110 | Рациональные уравнения | |
| 111 | Связь между площадями подобных фигур. Измерительные работы на местности | |
| 112 | Решение рациональных уравнений. | |
| 113 | Решение рациональных уравнений. | |
| 114 | Задачи на построение | |
| 115 | Контрольная работа №10 «Квадратные уравнения» | |
| 116 | Задачи на построение методом подобных треугольников | |
| 117 | Рациональные уравнения как математические модели реальных ситуаций |
|
| 118 | Решение текстовых задач алгебраическим способом |
|
| 119 | Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника | |
| 120 | Решение текстовых задач алгебраическим способом |
|
| 121 | Значения синуса, косинуса, тангенса для углов 30ْ, 45ْ, 60ْ, 90ْ | |
| 122 | Решение текстовых задач алгебраическим способом |
|
| 123 | Еще одна формула корней квадратного уравнения |
|
| 124 | Соотношения между сторонами и углами прямоугольного треугольника | |
| 125 | Еще одна формула корней квадратного уравнения |
|
| 126 | Решение задач на применение подобия треугольников | |
| 127 | Теорема Виета |
|
| 128 | Теорема Виета. Разложение квадратного трехчлена на линейные множители |
|
| 129 | Контрольная работа №9 «Подобие треугольников и соотношение между сторонами и углами прямоугольного треугольника» | |
| 130 | Контрольная работа №11 «Квадратные уравнения» | |
| 131 | Взаимное расположение прямой и окружности, двух окружностей. | |
| 132 | Иррациональные уравнения | |
| 133 | Иррациональные уравнения | |
| 134 | Касательная и секущая к окружности, равенство касательных, проведенных из одной точки. | |
| 135 | Иррациональные уравнения | |
| 136 | Метрические соотношения в окружности: свойства секущих и касательных. | |
| 137 | Числовые неравенства и их свойства | |
| 138 | Свойства числовых неравенств. | |
| 139 | Центральный угол. Центральный, вписанный угол. | |
| 140 | Замечательные точки треугольника |
|
| 141 | Величина вписанного угла. | |
| 142 | Свойства числовых неравенств. | |
| 143 | График функции, возрастание и убывание функции, промежутки знакопостоянства |
|
| 144 | Теорема об отрезках пересекающихся хорд. | |
| 145 | Исследование функций на монотонность | |
| 146 | Решение задач по теме «Центральные и вписанные углы» |
|
| 147 | Исследование функций на монотонность | |
| 148 | Решение линейных неравенств. |
|
| 149 | Свойство биссектрисы угла | |
| 150 | Линейные неравенства с одной переменной и их системы. | |
| 151 | Серединный перпендикуляр. Свойство серединного перпендикуляра к отрезку. | |
| 152 | Квадратные неравенства и их решение | |
| 153 | Решение квадратных неравенств | |
| 154 | Окружность, вписанная в треугольник | |
| 155 | Решение квадратных неравенств | |
| 156 | Описанные четырехугольники. Свойство описанного четырёхугольника | |
| 157 | Контрольная работа №13 «Неравенства» | |
| 158 | Приближенные значения действительных чисел. | |
| 159 | Описанная окружность. Окружность, описанная около треугольника | |
| 160 | Приближенные значения действительных чисел. | |
| 161 | Вписанные четырехугольники. Свойство вписанного четырёхугольника | |
| 162 | Стандартный вид положительного числа. |
|
| 163 | Повторение. Преобразование рациональных выражений. |
|
| 164 | Решение задач по теме «Окружность» |
|
| 165 | Повторение. Преобразование выражений, содержащих операцию извлечения квадратного корня |
|
| 166 | Решение задач по теме «Окружность» |
|
| 167 | Квадратные уравнения |
|
| 168 | Решение квадратных неравенств |
|
| 169 | Контрольная работа №12 «Окружность» | |
| 170 | Повторение. Четырёхугольники и их площади. |
|
| 171 | Повторение. Признаки подобия треугольников. | |
| 172 | Повторение. Окружность . | |
| 173 | Контрольная работа №14 «Итоговая контрольная работа» |
|
| 174 | Анализ контрольной работы | |
| 175 | Заключительный урок | |
Перечень учебно-методического обеспечения
Учебно-методический комплект по алгебре
1. «Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. -2-е изд.,испр. И доп.-М.:Мнемозина, 2009.».
3. Б.Г. Зив, В.М. Мейлер, А.П. Баханский. Задачи по геометрии для 7 – 11 классов. – М.: Просвещение, 2003.
4. С.М. Саакян, В.Ф. Бутузов. Изучение геометрии в 7-9 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2001.
5. Научно-теоретический и методический журнал «Математика в школе»
6. Еженедельное учебно-методическое приложение к газете «Первое сентября» Математика
7. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы: алгебра и геометрия 8класс. М.: ИЛЕКСА, 2005-2009
8. Алгебра. Тесты для промежуточной аттестации. 7-8 класс. Издание второе, переработанное. Под редакцией Ф.Ф. Лысенко. Ростов-на-Дону: Легион, 2007. – 160 с.
9. Дидактические материалы по алгебре для 8 класса – 5-е изд., перераб. Гусев В.А., Медяник А.И. – М.: Просвещение, 2000-2003.
10. Задачи повышенной трудности в курсе алгебры 7-9 классов: Книга для учителя. Н.П. Кострикина. – М.: Просвещение, 1991.
11. История математики в школе. VII-VIII кл. Пособие для учителей. / Г.И. Глейзер – М.: Просвещение, 1982 – 240 с.
12. Контрольные и самостоятельные работы по алгебре: 8 класс: к учебнику А.Г. Мордковича и др. "Алгебра. 7 класс" / М.А. Попов. – 2-е изд., стереотип. – М.: Издательство «Экзамен», 2008. – 63 с.
Кроме этого, используются:
Таблицы для уроков математики (Таблица «Квадратов двухзначных чисел» и т.д. из перечня таблиц);
Презентации для уроков – авторские разработки (Сайт «Математика на уроках и вне» http://matema.ucoz.ru/ )
Учебно-методический комплект по геометрии
Геометрия. Сборник рабочих программ. 7 – 9 классы: пособие для учителей общеобразовательных организаций / [автор-составитель Т.А. Бурмистрова. – М.: Просвещение, 2014
Контрольные работы по геометрии: 7 класс: к учебнику Л.С. Атанасяна и др. «Геометрия 7 – 9 классы» / Н.Б. Мельникова. – М.: Издательство «Экзамен», 2013
Тесты по геометрии: 7 класс: к учебнику Л.С. Атанасяна и др. «Геометрия 7 – 9 классы» / А.В. Фарков. – М.: Издательство «Экзамен», 2013
Дидактические материалы по геометрии: 7 класс: к учебнику Л.С. Атанасяна и др. «Геометрия 7 – 9 классы» / Н.Б. Мельникова, Г.А. Захарова. – М.: Издательство «Экзамен», 2014
Геометрия. 7 класс. Самостоятельные работ. Тематические тесты. Тесты для промежуточной аттестации. Справочник. Рабочая тетрадь / Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Издательство «Легион», 2013
Материально-техническое обеспечение.
Для учащихся
Алгебра.8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Н. П. Николаев. — М.: Мнемозина, 2009. — 191 с.\
Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — 13-е изд., испр. и доп. — М.: Мнемозина, 2009. — 270 с.
Геометрия, 7—9 классы: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и д. — М.: Просвещение, 2009.
Рабочая тетрадь по геометрии: 7 класс: к учебнику Л.С. Атанасяна и др. «Геометрия 7 – 9 классы» / Ю.А. Глазков, П.М. Камаев. – М.: Издательство «Экзамен», 2014
Кроме этого, для учащихся предоставлены:
Брошюры с печатной основой для самостоятельных и тестовых работ:
- тексты взяты из книги «Алгебра. 8 класс. Блицопрос: пособие для учащихся общеобразоват. учреждений / Е. Е. Тульчинская. — 4-е изд., испр. и доп. — М. : Мнемозина, 2008. — 128 с.»,
2). Брошюры/карточки с заданиями для контрольных работ
1. Комплект демонстрационных таблиц «Геометрия. 8 класс» к учебнику Л.С. Атанасяна / Т.Г. Ходот, Т.А. Бурмистрова, А.Ю. Ходот. – М.: Просвещение, 2014
2. Комплект таблиц «Математика. Геометрия. 7-11 класс». Наглядное пособие / М.: Спектр-М
3. CD - Диск «Уроки геометрии Кирилла и Мефодия»
4. CD - Диск «Геометрия 8 класс» / Издательство «1С», серия: «Школа»
Информационные источники
5. http://urokimatematiki.ru
6. http://intergu.ru/
7. http://karmanform.ucoz.ru
8. http://polyakova.ucoz.ru/
9. http://le-savchen.ucoz.ru/
10. http://www.it-n.ru/
11. http://www.openclass.ru/
12. http://festival.1september.ru/
Учебно-лабораторное оборудование
13. Мультимедийный компьютер
14 Мультимедиа проектор
15. Интерактивная доска
16. Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц
17. Комплект инструментов классных: линейка, транспортир, угольник (30, 60), угольник (45, 45), циркуль

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике за курс 8 класса (базовый уровень) (0.83 MB)
Рабочая программа по математике за курс 8 класса (базовый уровень) (0.83 MB)
 0
0 995
995 52
52 Нравится
0
Нравится
0



