Конспект урока по алгебре в 8 классе в рамках ФГОС ООО
Тема урока «Т. Виета»
Цель урока: сформулировать теорему Виета
Задачи:
1) организация совместной деятельности, нацеленной на предметный результат: сформулировать теорему Виета;
2) создание условий для развития умений сравнивать, выявлять закономерности, обобщать, учить думать, высказывать своё мнение;
3) воспитывать трудолюбие, аккуратность, умение работать в коллективе;
Формируемые УУД:
| личностные | познавательные | коммуникативные | регулятивные |
| *самоопределение, *смыслообразование | *общеучебные -формулирование цели -поиск и выделение информации *действия постановки и решения проблемы -формулирование проблемы -самостоятельное создание способов решения проблем поискового и творческого характера | *планирование -определение цели -способов взаимодействия партнеров *постановка вопросов -инициативное сотрудничество в поиске и сборе информации *управление поведением партнера, точностью выражать свои мысли -контроль, коррекция, оценка действий партнера, умение выражать свои мысли
| *целеполагание -постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще не известно *волевая саморегуляция -способность к волевому усилию преодоления препятствий -способность к мобилизации сил и энергии *оценка -осознание и выделение того, что уже известно и что еще подлежит усвоению -осознание качества и уровня усвоения *прогнозирование *контроль *коррекция *планирование -составление плана и последовательности действий
|
Структура урока:
1. Самоопределение к деятельности.
2. Актуализация знаний и фиксация затруднений в деятельности.
3. Выявление причин затруднений и постановка учебной цели.
4. Построение проекта выхода из затруднения.
5. Первичное закрепление во внешней речи
6. Самостоятельная работа с самопроверкой.
7. Включение новых знаний в систему знаний:
а) сравнение с текстом параграфа;
б) заучивание рассмотренного правила через его применение в простейших случаях;
в) ассоциативное запоминание
8. Домашнее задание:
9. Рефлексия урока
Начало урока.
На доске выведена пословица о математике:
«Математика-гимнастика ума»
- Но, кто такой гимнаст, и что такое гимнастика?
- Действительно, но что сегодня мы будем делать на уроке?
- Да, сегодня мы будем открывать новые знания…
- Вы любите математику? Тогда давайте вспомним прошлую тему, которую мы с вами изучали. «Квадратные уравнения»
- Полные, неполные? приведенные. Как они решаются?
- Молодцы!!!
А сейчас давайте решим уравнение х2-2087х+2086=0
- Как его решить? Можно ли не решая уравнение найти его корни?
Ребята пробуют способом подбора, с помощью калькулятора…
- Перед нами стоит задача и мы должны ее решить.
- запишите уравнение, корнями которого являются числа: 2 и 3.
Возникла проблема можно ли записать уравение, зная его корни?
На слайде уравнение х2-5х+6=0
- Давайте попытаемся определить знаки корней уравнений?
Ребята пробуют, но ничего не получается
Опять возникла проблема.
К сегодняшнему уроку вы должны были дома решить несколько приведенных уравнений . А сейчас давайте выпишем коэффициенты и корни каждого из уравнений
p q x1 x2
-3 -4 4 -1
-5 -14 -2 7
5 6 -2 -3
- давайте найдем связь между коэффициентами и корнями этих уравнений.
- действительно, х1+х2= -р, х1*х2 =q
Технологическая карта урока
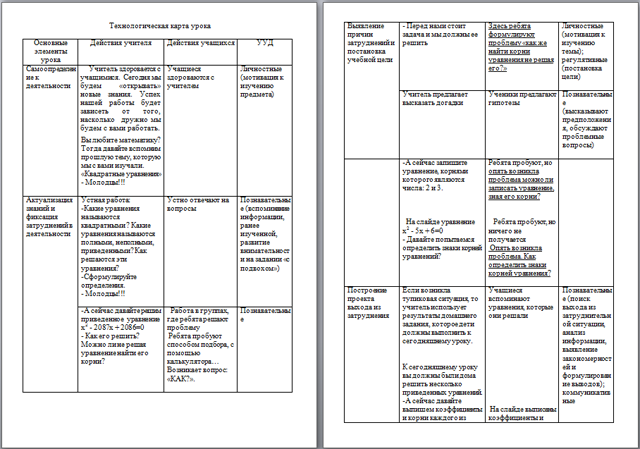
| Основные элементы урока | Действия учителя | Действия учащихся | УУД |
| Самоопределение к деятельности | Учитель здоровается с учащимися. Сегодня мы будем «открывать» новые знания. Успех нашей работы будет зависеть от того, насколько дружно мы будем с вами работать. Вы любите математику? Тогда давайте вспомним прошлую тему, которую мы с вами изучали. «Квадратные уравнения» - Молодцы!!!
| Учащиеся здороваются с учителем | Личностные (мотивация к изучению предмета) |
| Актуализация знаний и фиксация затруднений в деятельности | Устная работа: -Какие уравнения называются квадратными ? Какие уравнения называются полными, неполными, приведенными? Как решаются эти уравнения? -Сформулируйте определения. - Молодцы!!!
| Устно отвечают на вопросы | Познавательные (вспоминание информации, ранее изученной, развитие внимательности на задании «с подвохом») |
| -А сейчас давайте решим приведенное уравнение х2 - 2087х + 2086=0 - Как его решить? Можно ли не решая уравнение найти его корни?
| Работа в группах, где ребята решают проблему Ребята пробуют способом подбора, с помощью калькулятора… Возникает вопрос: «КАК?».
| Познавательные
|
| Выявление причин затруднений и постановка учебной цели
| - Перед нами стоит задача и мы должны ее решить | Здесь ребята формулируют проблему «как же найти корни уравнения не решая его?» | Личностные (мотивация к изучению темы); регулятивные (постановка цели)
|
| Учитель предлагает высказать догадки | Ученики предлагают гипотезы | Познавательные (высказывают предположения, обсуждают проблемные вопросы)
|
|
| -А сейчас запишите уравнение, корнями которого являются числа: 2 и 3.
На слайде уравнение х2 - 5х + 6=0 - Давайте попытаемся определить знаки корней уравнений?
| Ребята пробуют, но опять возникла проблема можно ли записать уравнение, зная его корни?
Ребята пробуют, но ничего не получается Опять возникла проблема. Как определить знаки корней уравнения?
|
|
| Построение проекта выхода из затруднения | Если возникла тупиковая ситуация, то учитель использует результаты домашнего задания, которое дети должны выполнить к сегодняшнему уроку.
К сегодняшнему уроку вы должны были дома решить несколько приведенных уравнений. -А сейчас давайте выпишем коэффициенты и корни каждого из уравнений, предложенных для домашнего решения: х2 – 3х – 4=0 х2 – 5х – 14 = 0 х2 + 5х – 6 = 0
- давайте найдем связь между коэффициентами и корнями этих уравнений. - действительно, х1+ х2= - р, х1* х2 = q
- А как быть, если уравнение не приведенное?
| Учащиеся вспоминают уравнения, которые они решали
На слайде выписаны коэффициенты и корни уравнений p q x1 x2 -3 -4 4 -1 -5 -14 -2 7 5 6 -2 -3
Дети ищут связь между корнями уравнений и коэффициентами уравнений
Ребята отвечают на поставленный вопрос. | Познавательные (поиск выхода из затруднительной ситуации, анализ информации, выявление закономерностей и формулирование выводов); коммуникативные |
| Формулировка темы урока |
Эту закономерность заметил знаменитый французский математик Франсуа Виет (1540–1603 г.). Теорема названа в честь этого математика. Учитель формулирует правило, а затем цель и тему урока.
Теорема Виета: «Если х1 и х2 корни приведенного квадратного уравнения х2 + px + q = 0, то х1 • х2 = q, а х1 + х2 = – p.»
| Далее учащиеся формулируют правило, которое они «открыли»: это связь между коэффициентами квадратного уравнения и его корнями. | Познавательные (анализируют новую информацию и полученные результаты, выявляют закономерности и формулируют правила умножения двух чисел с разными знаками; применяют математический язык для решения задач, изображают правило в виде схемы); коммуникативные
|
| а) сравнение с текстом параграфа;
| Предлагает сравнить сказанное с текстом параграфа в учебнике. | Работа с текстом учебника. Выделение сведений, о которых не говорилось учителем, ответы на вопросы учащихся. | Регулятивные УУД, направленные на формирование умения оценивать (сравнивать с эталоном) результаты деятельности; коммуникативные |
| б) первичное закрепление рассмотренного правила через его применение в простейших случаях | Просит решить несколько примеров из учебника
| Записывают в тетрадь примеры решают их, сразу проверяют себя, | Коммуникативные (отработка нового материала в речи и письме) Регулятивные(контроль выполненной работы) |
| Самостоятельная работа с самопроверкой
| Индивидуальная самостоятельная работа . По желанию детей выставляет отметки за работу на уроке в журнал | Решают и в парах сразу же контролируют и оценивают себя | Регулятивные (контроль выполненной работы) Личностные УУД: умение оценивать собственную учебную деятельность: свои достижения, самостоятельность, инициативу, ответственность, причины неудач
|
| Домашнее задание
| № 575 (a, в, д, е), № 577, № 586. Отвечать на контрольные вопросы 4, 5 (стр. 125). | Рассматривают, что задано, задают вопросы, записывают д.з. в дневники | Личностные, регулятивные |
| Рефлексия урока
| Что нового узнали на уроке? Как нашли выход из затруднительной ситуации? | Ученики отвечают на вопросы. | Личностные УУД: умение анализировать и характеризовать эмоциональные состояния в связи с изучением новой темы; оценивать собственную учебную деятельность: свои достижения, самостоятельность, инициативу, ответственность, причины неудач
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по алгебре на тему «Теорема Виета» (69 КB)
Конспект урока по алгебре на тему «Теорема Виета» (69 КB)
 0
0 516
516 52
52 Нравится
0
Нравится
0


