Решение логарифмических уравнений различными способами
| методы решения | образцы решения | ||||||||||||||
| по определению логарифма
| 1) Ответ: 4.
2) ОДЗ: Ответ: -1. | 3) Проверка: 1) 2) Ответ:2. | 4)
Ответ: 1, -8.
| ||||||||||||
| метод потенцирования
переход от равенства к равенству | 1) Проверка: 1)
-3 посторонний корень 2) Ответ: 2.
| 2) Проверка: 1) 2) Ответ: -1. | 3) Проверка: 1) -4 посторонний корень 2) 6 посторонний корень Ответ: уравнение корней не имеет. | ||||||||||||
| приведение логарифмического уравнения к квадратному
1) ввести новую переменную 2) решить уравнение 3) выполнить обратную подстановку и решить уравнения относительно х | 1) Ответ: | 2) Ответ: 125; | 3) Ответ: 10. | ||||||||||||
| приведение логарифмов к одному основанию
формула перехода к новому основанию | 1) Проверка: | 2) умножим всё уравнение на y Проверка: 1) Ответ: 25,
|
| ||||||||||||
| логарифмирование обеих частей уравнения
| 1) Проверка: 1) 2) Ответ: 3, | 2) Проверка: 1) 2) Ответ: 0,001 ; 10.
| 3) Проверка: 1) 2) Ответ: 100; 0,1.
| ||||||||||||
| графический метод
где Построить в одной системе координат графики функций
| 1) Y а)
б)
Ответ:
|
| |||||||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход



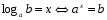
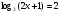
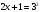
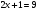
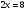
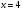
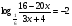
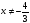
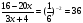
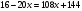
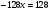
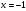
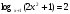
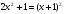
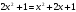
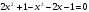
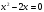
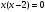
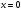 или
или 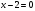
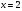
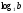 не существует
не существует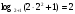









 Способы решения логарифмических уравнений (236.59 KB)
Способы решения логарифмических уравнений (236.59 KB)
 0
0 244
244 4
4 Нравится
0
Нравится
0


