
ГАОУ СПО НСО «Барабинский медицинский колледж» Решение задач по теме: «Показательная и логарифмическая функции» Преподаватель: Вашурина Т. В. Барабинск, 2015

Цель урока:
- Повторить виды показательных и логарифмических уравнений и неравенств и методы их решения.
- Закрепить навыки решения показательных и логарифмических уравнений и неравенств.

Фронтальный опрос
1. Дайте определение простейшего логарифмического неравенства
2. Дайте определение логарифмического уравнения
3. Перечислите способы решения логарифмических уравнений
 0, a≠1, х – любое число, называют показательной функцией . Свойства: Область определения показательной функции: D (y)= R – множество всех действительных чисел . Область значений показательной функции: E (y)= R + - множество всех положительных чисел . Показательная функция y=a x возрастает при a1 . Показательная функция y=a x убывает при 0 . " width="640"
0, a≠1, х – любое число, называют показательной функцией . Свойства: Область определения показательной функции: D (y)= R – множество всех действительных чисел . Область значений показательной функции: E (y)= R + - множество всех положительных чисел . Показательная функция y=a x возрастает при a1 . Показательная функция y=a x убывает при 0 . " width="640"
Определение: Функцию вида y=a x , где а0, a≠1, х – любое число, называют показательной функцией .
Свойства:
- Область определения показательной функции: D (y)= R – множество всех действительных чисел .
- Область значений показательной функции: E (y)= R + - множество всех положительных чисел .
- Показательная функция y=a x возрастает при a1 .
- Показательная функция y=a x убывает при 0 .
 0, a ≠ 1 и уравнения, сводящиеся к этому виду. " width="640"
0, a ≠ 1 и уравнения, сводящиеся к этому виду. " width="640"
Решение показательных уравнений
- Определение: Показательным уравнением называется уравнение вида а х = b, где a 0, a ≠ 1 и уравнения, сводящиеся к этому виду.

Методы решения показательных уравнений :
- а) Метод уравнивания оснований .
- б) Метод вынесения общего множителя за скобки.
- в) Метод введения вспомогательной переменной
- г) Графический метод, метод подбора
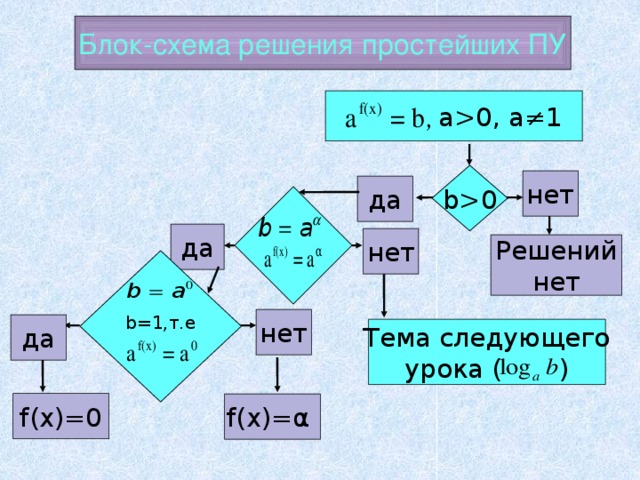 0, a≠1 b0 нет да да нет Решений нет b=1,т.е нет да Тема следующего урока ( ) f(x)=0 f(x)=α 7 " width="640"
0, a≠1 b0 нет да да нет Решений нет b=1,т.е нет да Тема следующего урока ( ) f(x)=0 f(x)=α 7 " width="640"
Блок-схема решения простейших ПУ
a0, a≠1
b0
нет
да
да
нет
Решений
нет
b=1,т.е
нет
да
Тема следующего
урока ( )
f(x)=0
f(x)=α
7
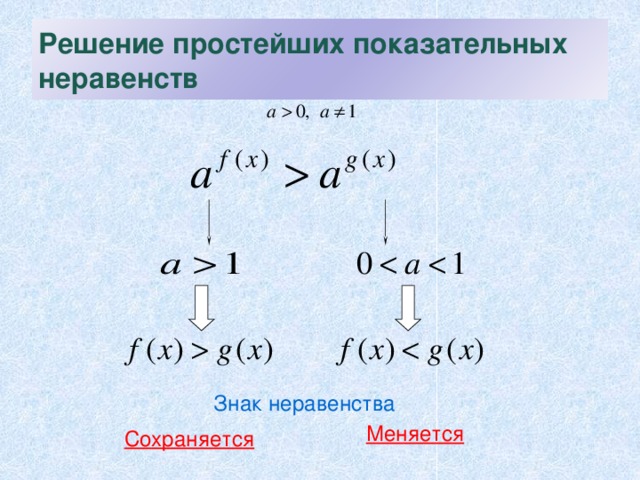
Решение простейших показательных неравенств
Знак неравенства
Меняется
Сохраняется
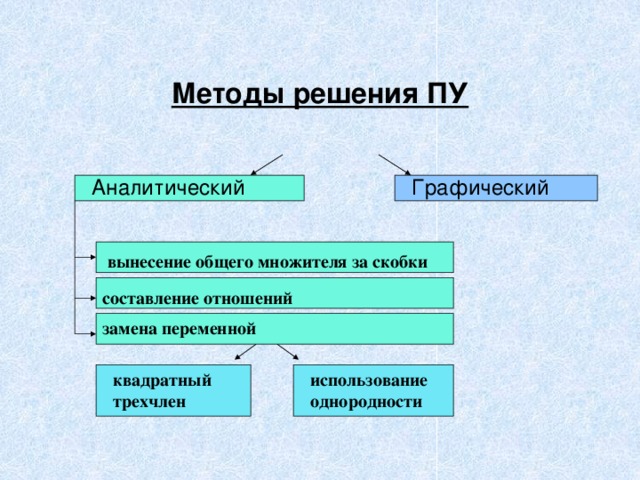
Методы решения ПУ
Аналитический
Графический
вынесение общего множителя за скобки
составление отношений
замена переменной
использование
квадратный
однородности
трехчлен

- Логарифмическая функция 1. Какая функция называется логарифмической функцией? 2. Область определения и область значения логарифмической функции. 3. Когда логарифмическая функция возрастает, когда убывает? 4. Является ли логарифмическая функция четной, нечетной.?

Логарифмические уравнения
Определение:
Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.

Методы решения ЛУ:
1.Применение определения логарифма
2. Введение
Вид уравнения
новой переменной
3. Приведение к одному и тому же основанию
4. Метод потенцирования
5. Метод логарифмирования обеих частей уравнения
6. Функционально-графический метод

Неравенство, содержащее переменную только под знаком логарифма, называется логарифмическим.
 1 x1 x2 0 1. 0 x2 x1 0 a 1 x2 x1 0 2. 0 x1 x2 0 " width="640"
1 x1 x2 0 1. 0 x2 x1 0 a 1 x2 x1 0 2. 0 x1 x2 0 " width="640"
Свойства логарифмических неравенств:
a 1
x1 x2 0
1.
0
x2 x1 0
a 1
x2 x1 0
2.
0
x1 x2 0

ПОМНИ:
При решении логарифмических неравенств следует учитывать общие свойства неравенств, свойство монотонности логарифмической функции и область её определения.

Выполнение упражнений
- учебник Алгебра и начала математического анализа. под ред. А. Н. Колмогорова:
- стр. 231 № 463 (в, г), 464 (а, б), 467 (в, г)
- стр. 244 № 519 (в, г), 520 (а, б).

Самостоятельная работа
Время выполнения: 15 минут
Критерии оценки:
- «5» баллов –5 верно выполненных заданий
- «4» балла – 4 верно выполненных задания
- «3» балла – 3 верно выполненных задания
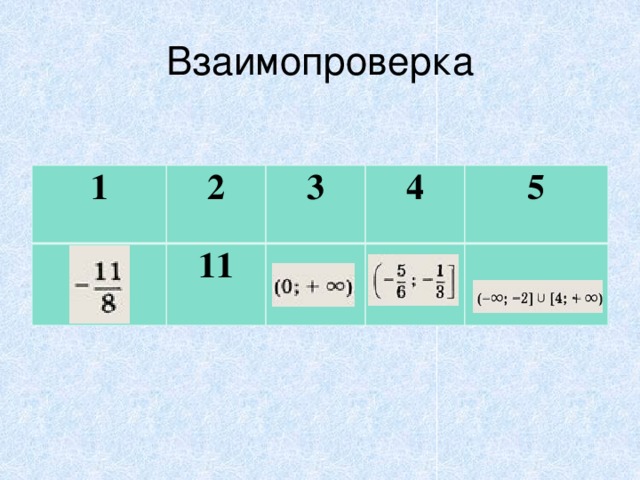
Взаимопроверка
1
2
3
11
4
5

Оценивание, выставление оценок
Критерии оценки:
- «5» баллов – 5 верно выполненных заданий
- «4» балла – 4 верно выполненных задания
- «3» балла – 3 верно выполненных задания

Домашнее задание
Учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмогорова, 10-11 классы:
стр.231 № 464 (в, г), стр. 244 № 520 (в, г)
Работа с электронным приложением к учебнику «Алгебра 10-11» , работа с конспектом лекции.

Спасибо за внимание!


 Получите свидетельство
Получите свидетельство Вход
Вход






 0, a≠1, х – любое число, называют показательной функцией . Свойства: Область определения показательной функции: D (y)= R – множество всех действительных чисел . Область значений показательной функции: E (y)= R + - множество всех положительных чисел . Показательная функция y=a x возрастает при a1 . Показательная функция y=a x убывает при 0 . " width="640"
0, a≠1, х – любое число, называют показательной функцией . Свойства: Область определения показательной функции: D (y)= R – множество всех действительных чисел . Область значений показательной функции: E (y)= R + - множество всех положительных чисел . Показательная функция y=a x возрастает при a1 . Показательная функция y=a x убывает при 0 . " width="640"
 0, a ≠ 1 и уравнения, сводящиеся к этому виду. " width="640"
0, a ≠ 1 и уравнения, сводящиеся к этому виду. " width="640"

 0, a≠1 b0 нет да да нет Решений нет b=1,т.е нет да Тема следующего урока ( ) f(x)=0 f(x)=α 7 " width="640"
0, a≠1 b0 нет да да нет Решений нет b=1,т.е нет да Тема следующего урока ( ) f(x)=0 f(x)=α 7 " width="640"






 1 x1 x2 0 1. 0 x2 x1 0 a 1 x2 x1 0 2. 0 x1 x2 0 " width="640"
1 x1 x2 0 1. 0 x2 x1 0 a 1 x2 x1 0 2. 0 x1 x2 0 " width="640"
















 Презентация по математике "Решение задач по теме «Показательная и логарифмическая функции»" (0.19 MB)
Презентация по математике "Решение задач по теме «Показательная и логарифмическая функции»" (0.19 MB)
 0
0 708
708 82
82 Нравится
0
Нравится
0


