Синус, косинус, тангенс угла

СИНУС, КОСИНУС, ТАНГЕНС, КОТАНГЕНС

27.12.21

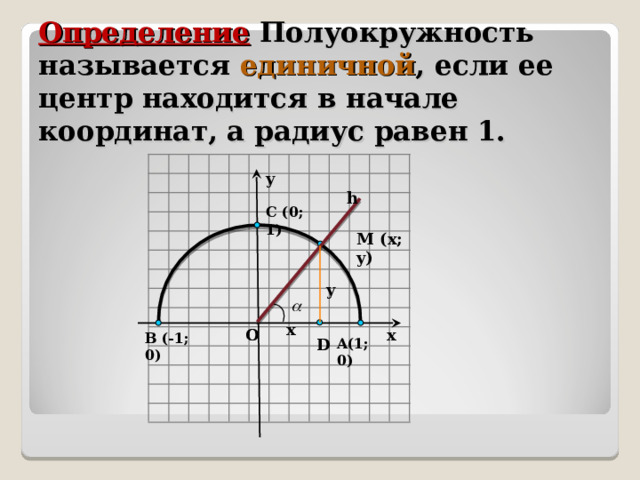
Определение Полуокружность называется единичной , если ее центр находится в начале координат, а радиус равен 1.

y

h

C (0; 1)

M (x; y)

y

x

x

O

B (-1; 0)

A(1; 0)

D

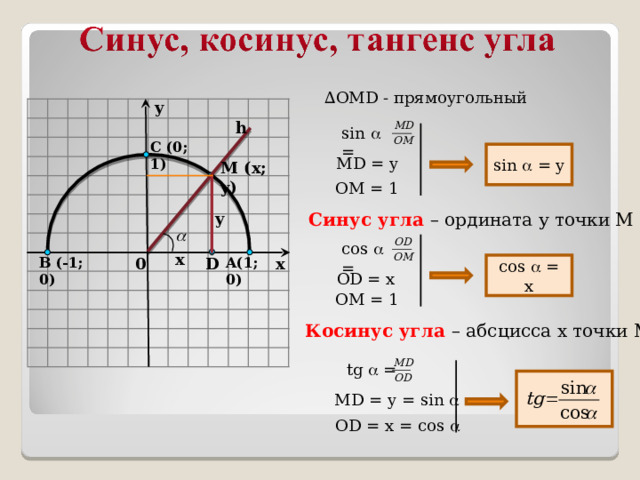
∆ OMD - прямоугольный

y

h

sin  =

C (0; 1)

sin  = y

MD = y

M (x; y)

OM = 1

Синус угла – ордината у точки М

y

cos  =

x

0

x

B (-1; 0)

D

A(1; 0)

cos  = x

OD = x

OM = 1

Косинус угла – абсцисса х точки М

tg  =

MD = y = sin 

OD = x = cos 

y

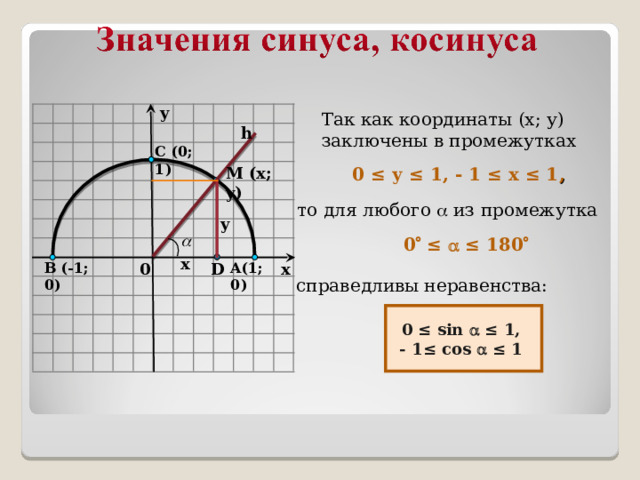
Так как координаты (х; у) заключены в промежутках

h

C (0; 1)

0 ≤ у ≤ 1, - 1 ≤ х ≤ 1 ,

M (x; y)

то для любого  из промежутка

y

0  ≤  ≤ 180 

x

D

0

x

A(1; 0)

B (-1; 0)

справедливы неравенства:

0 ≤ sin  ≤ 1,

- 1≤ cos  ≤ 1

y

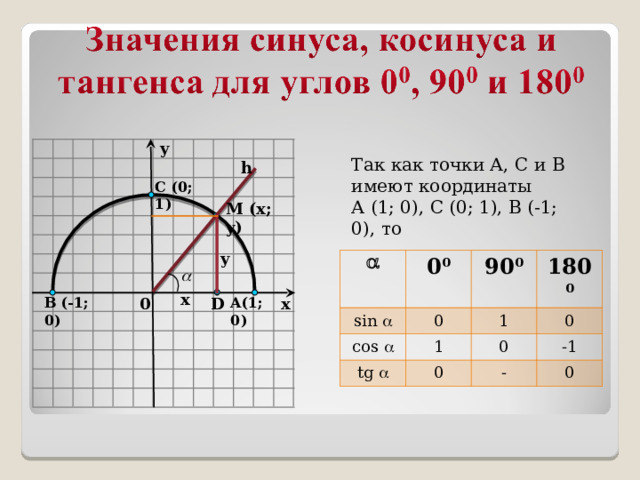
Так как точки А, С и B имеют координаты

А (1; 0), С (0; 1), В (-1; 0), то

h

C (0; 1)

M (x; y)

y



sin 

0 0

90 0

cos 

0

180 0

tg 

1

1

0

0

0

-

-1

0

x

A(1; 0)

D

B (-1; 0)

0

x

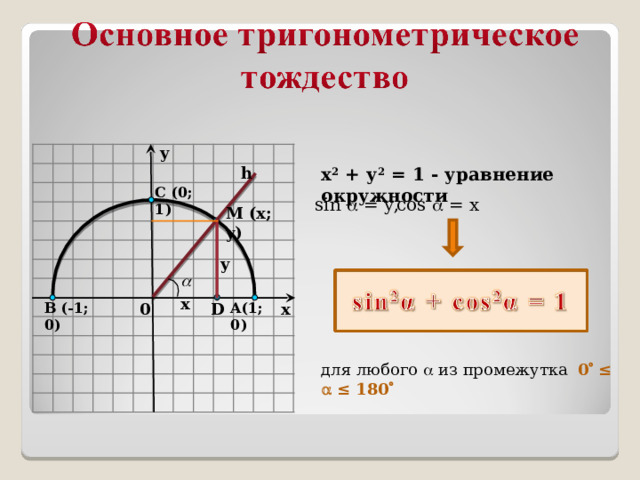
y

х 2 + у 2 = 1 - уравнение окружности

h

C (0; 1)

cos  = x

sin  = y ,

M (x; y)

y

x

D

0

x

A(1; 0)

B (-1; 0)

для любого  из промежутка 0  ≤  ≤ 180 

sin (90  -  ) = cos 

cos (90  -  ) = sin 

при 0  ≤  ≤ 90 

sin (180  -  )= sin 

cos (180  -  ) = - cos 

при 0  ≤  ≤ 180 

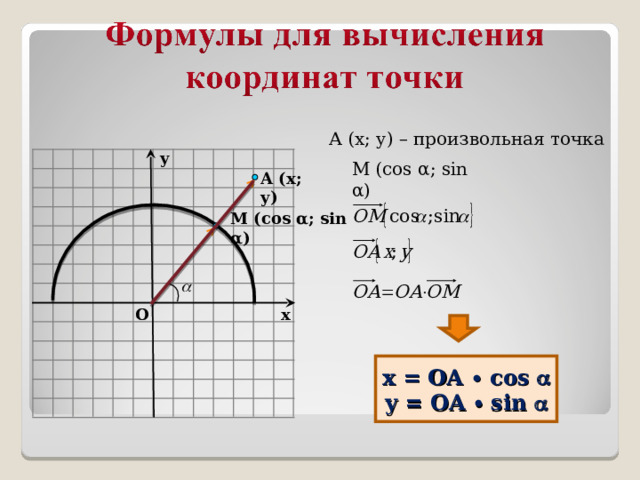
А (x; y) – произвольная точка

y

М (сos α; sin α)

A (x; y)

M (cos α ; sin α )

O

x

x = ОА ∙ cos 

y = OA ∙ sin 

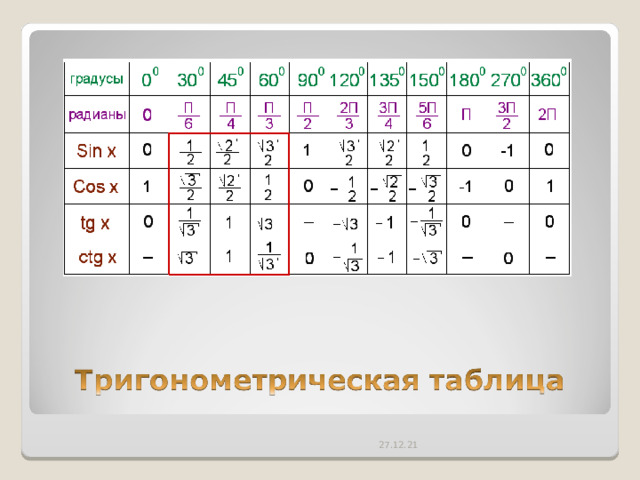
Составить таблицу:

27.12.21

27.12.21

• Решить № 1012
• № 1013

Закрепление

27.12.21

• Решение № 1012.
• Точка с координатами ( х ; у ) принадлежит единичной полуокружности, если выполняются условия: –1≤ х ≤1, –1≤ у ≤1 и х 2 + у 2 = 1.
• Точка М 1 (0; 1) удовлетворяет всем условиям → она лежит на единичной полуокружности.
• Точка М 2 удовлетворяет всем условиям → она лежит на единичной полуокружности.
• Точки М 3 , М 4 , А (1; 0), В (–1; 0) также лежат на единичной

полуокружности.

• Синус АОМ – это ордината точки М . Косинус АОМ – это абсцисса точки М . Тангенс АОМ равен отношению синуса АОМ к его косинусу.

М 1 (0; 1) → sinАОМ 1 = 1, cosАОМ 1 = 0, tgАОМ 1 = 0.

• М 2 → sinАОМ 2 = , cosАОМ 2 = , tgАОМ 2 = : = √3
• М 3 → sinАОМ 3 = , cosАОМ 3 = , tgАОМ 3 =
• М 4 → sinАОМ 4 = , cosАОМ 4 = , tgАОМ 4 =

27.12.21

Решение:

• sin 2 a + cos 2 a = 1 → sina = , но так как 0 ≤sina ≤1 → sin a = .
• а) cos a = → sina =
• б) cos a = → sina =
• в) cos a = –1 → sina = 0.
• Ответ: а) ; б) ; в) 0

№ 1013.

27.12.21

• изучить материал пунктов 97–99;
• ответить на вопросы 1–4, с. 266;
• решить задачи № 1014, 1015

Домашнее задание:

27.12.21