Презентация по математике по теме "Тригонометрические функции произвольного угла"

Цели урока:

- Образовательные – ввести понятие синус, косинус, тангенс угла от 0° до 180°, вывести основное тригонометрическое тождество и формулы для вычисления координат точки, рассмотреть формулы приведения.

- Развивающие – формирование понятия о синусе, косинусе, тангенсе как функциях от угла, области определения тригонометрических функций, развитие логического мышления, развитие правильной математической речи.

- Воспитательные – развитие навыка самостоятельной работы, культуры поведения, аккуратности в ведении записей.

Актуализация опорных знаний

- Какие могут быть углы?

- Как называются стороны прямоугольного треугольника?

- Какая сторона треугольника называется катетом?

- Какая сторона треугольника называется гипотенузой?

- Какие соотношения между сторонами и углами этого треугольника вы знаете?

Полную информацию смотрите в файле. 

Алгебра 9 класс

Урок подготовила учитель математики

общеобразовательной средней школы –гимназии №2

г.Актобе

Власова Наталья Николаевна

Урок по теме

«Тригонометрические функции произвольного угла»

Цели урока:

• Образовательные – ввести понятие синус, косинус, тангенс угла от 0° до 180°,вывести основное тригонометрическое тождество и формулы для вычисления координат точки, рассмотреть формулы приведения.
• Развивающие – формирование понятия о синусе, косинусе, тангенсе как функциях от угла, области определения тригонометрических функций, развитие логического мышления, развитие правильной математической речи.
• Воспитательные – развитие навыка самостоятельной работы, культуры поведения, аккуратности в ведении записей.

Актуализация опорных знаний

• Какие могут быть углы?
• Как называются стороны прямоугольного треугольника?
• Какая сторона треугольника называется катетом?
• Какая сторона треугольника называется

гипотенузой?

• Какие соотношения между сторонами и углами этого треугольника вы знаете?

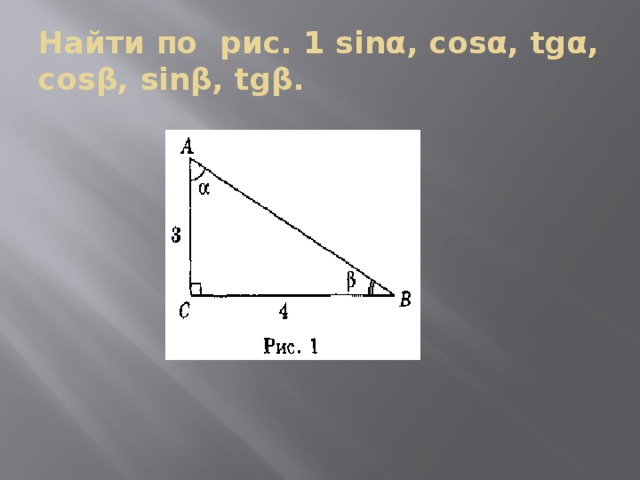
Найти по рис. 1 sinα, cosα, tgα, cosβ, sinβ, tgβ.

Изучение нового материала

• Определим значения синуса, косинуса и тангенса для любого угла от 0° до 180°.
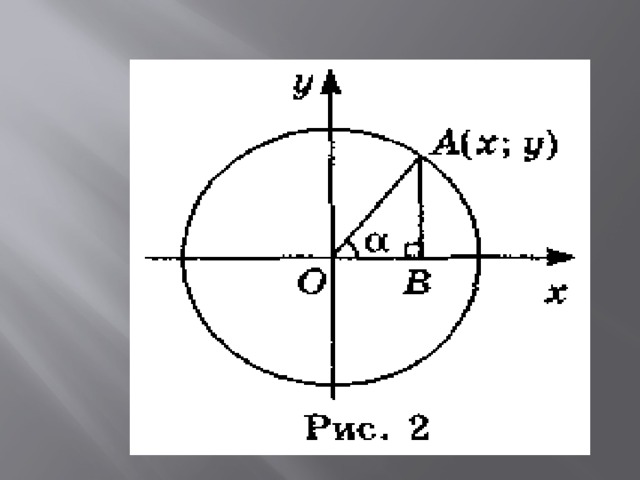
• Возьмем окружность на плоскости ху с центром в начале координат и радиусом R.

0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно: " width="640"

• Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y0) угол а.
• Пусть х и у — координаты точки А.

Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно:

• sinα = АВ⁄ОА = у⁄1= у

• cosα =ОВ/ОА = Х/1 = x ;

• tg α = АВ/ОВ = У/Х

• сtg α = ОВ/АВ = Х/у

Определения

• Синусом произвольного угла называется отношение ординаты точки А к радиусу
• Косинусом произвольного угла называется отношение абсциссы точки А к радиусу

• Пользуясь определением, для любого угла α,

0°

sin 0° = 0, cos 0° = 1, tg 0° = 0; sin 180° = 0,

cos 180° = -l, tg 180° = 0.

• Из курса геометрии известно, что для любого острого угла α:

Sin(90°- α)= cos α, cos (90°- α)= Sin α.

Основное тригонометрическое тождество

0), абсцисса — отрицательная ( cosα тогда отношение ординаты к абсциссе — отрицательное (tgα " width="640"

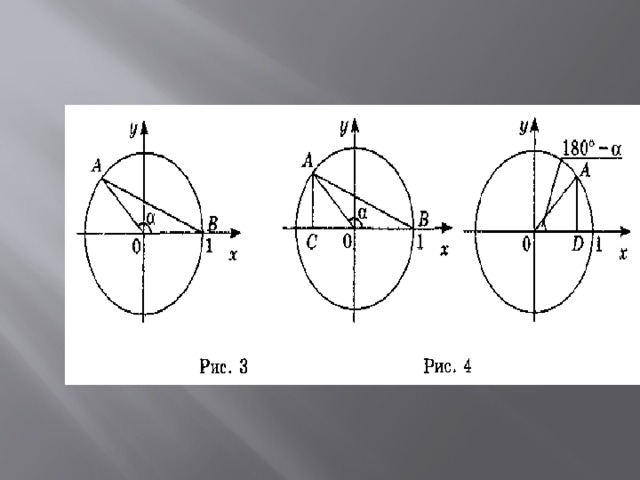
Если α — тупой (0°

• то ордината точки А (рис. 3) положительная

( sin α 0),

• абсцисса — отрицательная ( cosα

тогда отношение ординаты к абсциссе — отрицательное (tgα

• Если α – тупой угол

• cos α = -cos (180°- α),

• sinα = sin (180° - α),

• tg α = -tg(180° - α).

Например

• sin 120° = sin (180° - 120°) = sin 60° =√3/2 ,

• cos 150 o = - cos (180° - 150°) = - cos 30° = -½ ,

• tg 135° = -tg (180° - 135°) = - tg 45° = - 1.

Закрепление нового материала

Решить № 275, 278, 2 80 (а, б)

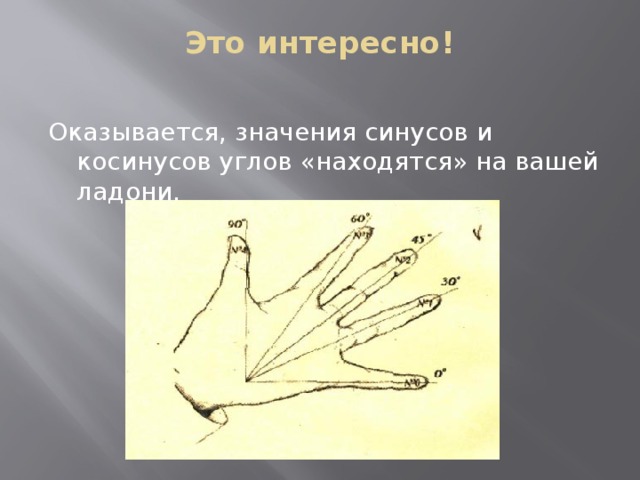
Это интересно!

Оказывается, значения синусов и косинусов углов «находятся» на вашей ладони.

Введем нумерацию пальцев:

мизинец № 0 – соответствует 0,

безымянный № 1 – соответствует 30,

средний № 2 – соответствует 45,

указательный № 3 – соответствует 60,

большой № 4 – соответствует 90.

Самостоятельная работа учащихся

1 вариант № 280 а ,286

2 вариант № 280 б ,288

Домашнее задание

Выучить § 17, решить № 282,283 Вопросы с.126.

Подготовить сообщение « Из истории тригонометрии».

Что вы узнали нового на уроке:

• вы рассматривали …
• вы анализировали …
• вы получили …
• вы сделали вывод …
• вы пополнили словарный запас следующими терминами …

Спасибо за урок!