Получите свидетельство
Вход
Цели:
Образовательные – научить учащихся сравнивать значения тригонометрических функций, если углы заданы в радианах с помощью тригонометрического круга ;
повторить определения синуса, косинуса, тангенса и котангенса; четность и нечетность тригонометрических функций; формулы приведения;
Развивающие - развитие познавательных способностей учащихся, их способностей к самообучению; расширить сферу математических знаний,
Воспитательные - формирование умений саморегулирования своей учебно - познавательной деятельности.
Оборудование:
- компьютер, интерактивная доска, тригонометрический круг,
- презентация,
- раздаточный материал: листы А4 с заданиями к уроку
Ход урока.
1. Подготовка к восприятию нового материала.
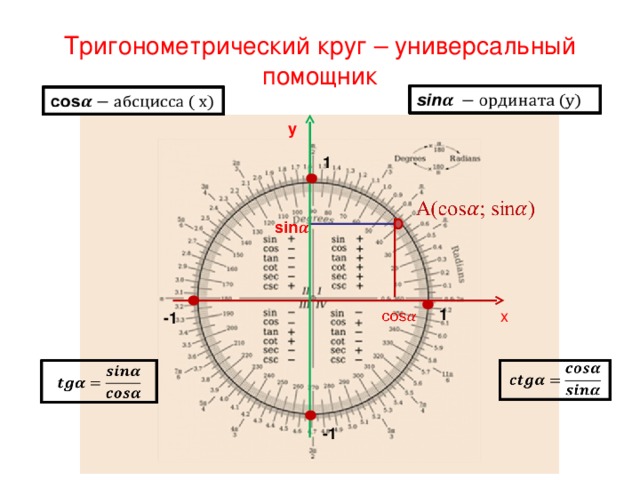
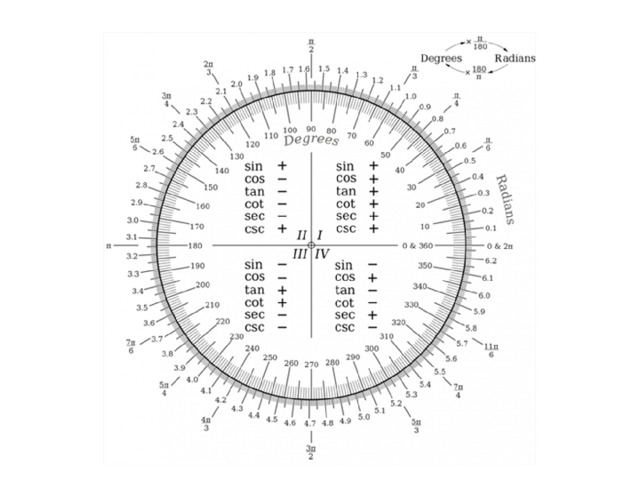
Тригонометрический круг мощный и универсальный помощник во всех разделах тригонометрии. Школьный курс математики знакомит нас с двумя основными мерами углов: градусной и радианной. Сегодня тригонометрический круг нам будет помогать сравнивать значения тригонометрических функций, если углы выражены не градусами, а радианами. В тестах по ЕНТ встречаются задания вида: Расположите числа в порядке возрастания sin1, 6; cos1, 6; cos( - 3, 5).
Для успешной работы нам нужно знать : Что такое синус, косинус, тангенс и котангенс, формулы приведения. Синусом числа а называется ордината точки, изображающей это число на числовой окружности. Синусом угла в а радиан называется синус числа а. Синус - функция нечетная . Область определения: х ( - ∞ ; +∞ )
Косинусом числа а называется абсцисса точки, изображающей это число на числовой окружности. Косинусом угла в а радиан называется косинус числа а. Косинус - функция четная. . Область определения: х ( - ∞ ; +∞ )
Тангенсом числа называется отношение синуса этого числа к косинусу этого числа: . Тангенс - функция нечетная . Область определения: х
Котангенсом числа называется отношение косинуса этого числа к синусу этого числа: . Котангенсом угла в а радиан называется котангенс числа а.
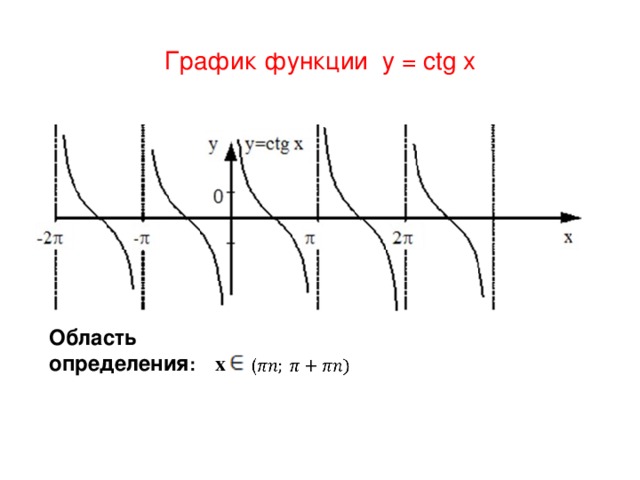
Котангенс - функция нечетная Область определения: х (0+πn; π+πn)
Изучение нового материала. У вас на столах модель тригонометрическиго круга, где углы выражены радианами. Именно этот круг будет нам помогать в работе.
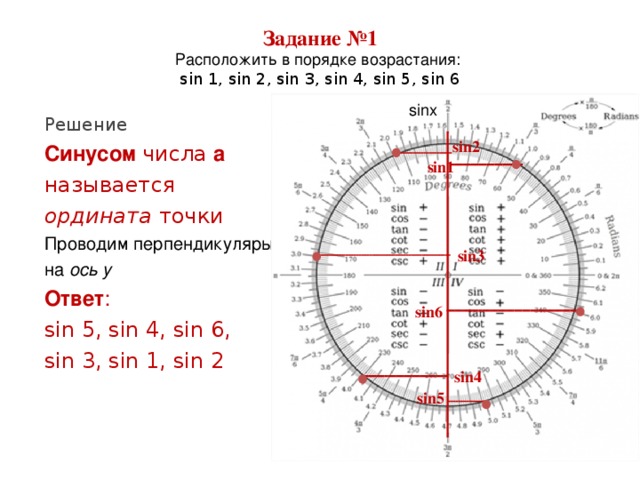
Задание 1. Расположите числа в порядке возрастания: sin 1, sin 2, sin 3, sin 4, sin 5,
sin 6. Круг наглядно позволяет определять значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их. Поскольку синус — это ордината соответствующей точки на единичной окружности, то для нахождения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6 достаточно определить значение y в точках 1, 2, 3, 4, 5 и 6 радиан. Проводим перпендикуляры на ось у
Ответ: sin 5; sin 4; sin 6; sin 3; sin 1; sin 2
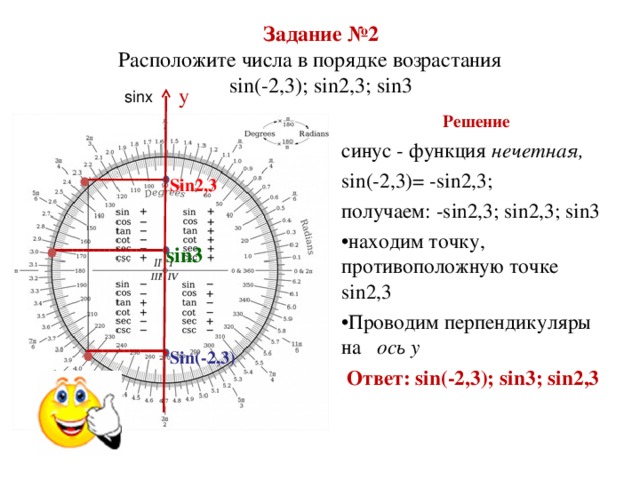
Пример 2. Расположите числа в порядке возрастания sin( - 2, 3); sin2, 3; sin3.
Т. к. синус - функция нечетная , получаем - sin2, 3; sin2, 3; sin3.
С помощью простой геометрической операции - прикладывания линейки, находим точку, симметричную точке sin2, 3. Отмечаем точку sin( - 2, 3)
Ответ: sin( - 2, 3); sin3; sin2, 3
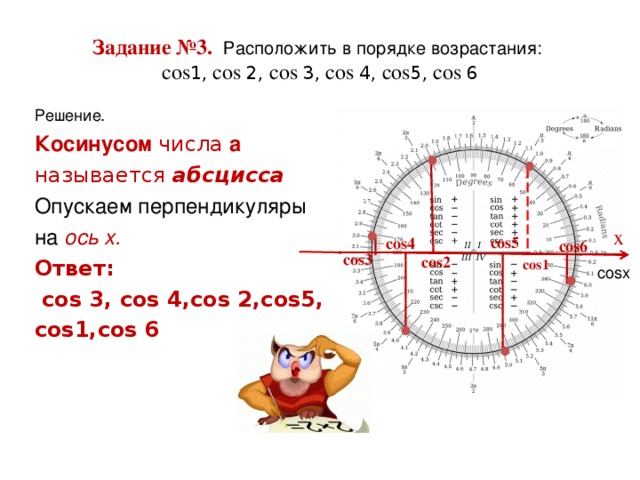
Пример 3. Расположите числа в порядке возрастания: cos 1, cos 2, cos 3, cos 4, cos 5, cos 6.
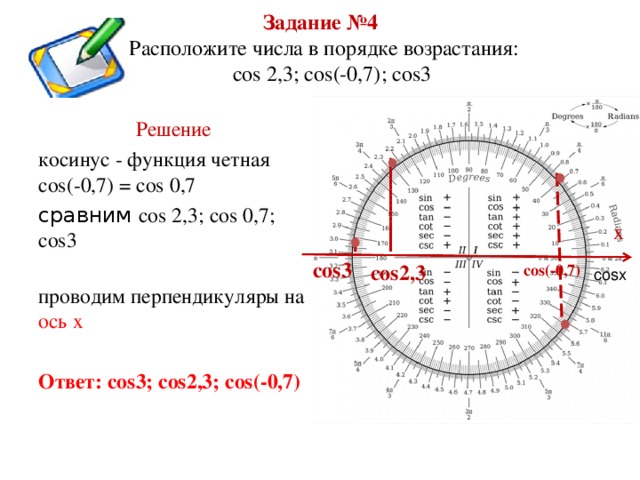
Пример 4. Расположите числа в порядке возрастания: cos 2, 3; cos( - 0, 7); cos3
Косинус - функция четная . Поэтому, получаем cos( - 0, 7) = cos 0, 7
Формулами приведения называются формулы, выражающие тригонометрические функции углов 90° 180° , 270° , 360° через тригонометрические функции угла α.
Этих формул 32 !!! Не пугайтесь, учить их не надо, надо лишь запоминать «ключики» или законы
Итак, необходимо уяснить «закон», который здесь работает:
1. Четверть
2. Знак функции в соответствующей четверти
3. Название
Мы знаем, что при π , 2π функция на кофункцию не изменяется
Значит, при 3, 14 и 6, 28 функция на кофункцию не изменяется
При функция изменяется на кофункцию.
Значит, при 1, 57 и 4, 71 функция изменяется на кофункцию
Теперь по представленному закону составим таблицу формул приведения
Например:
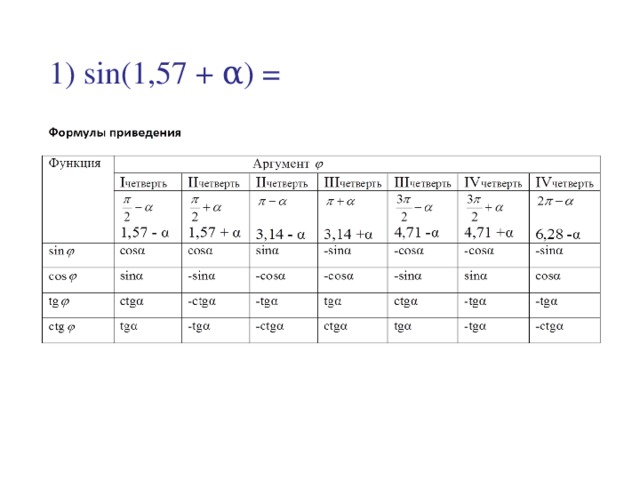
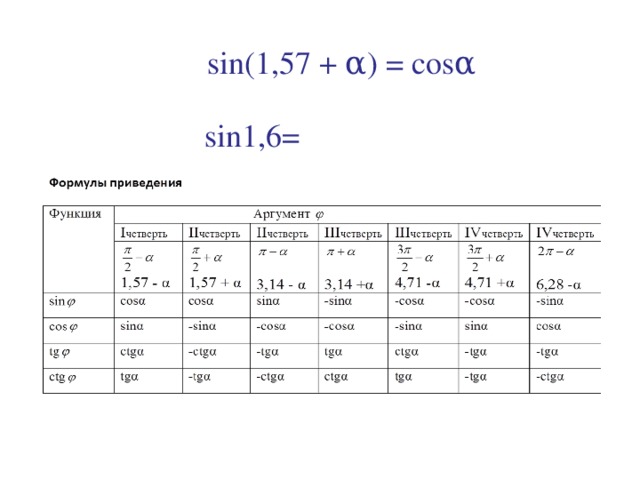
1). sin(1, 57 + α) = cosα
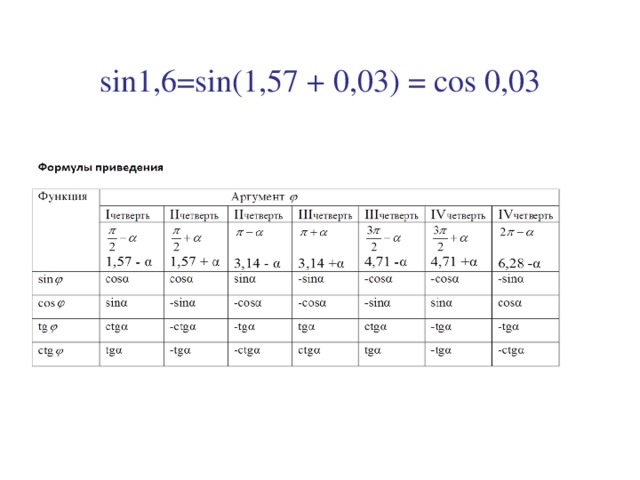
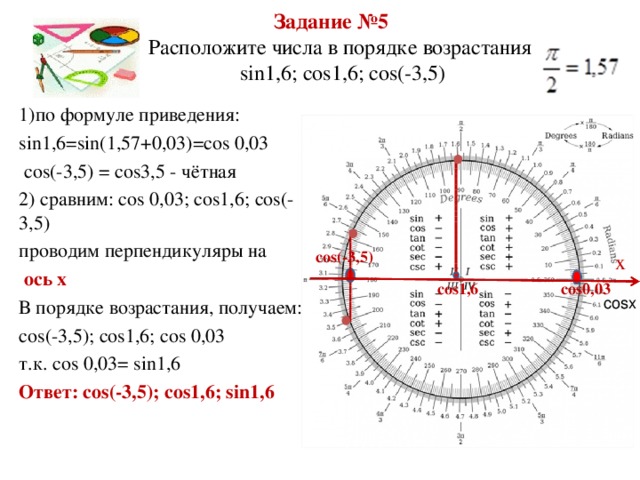
sin 1, 6 = sin(1, 57 +0, 03) = cos 0, 03
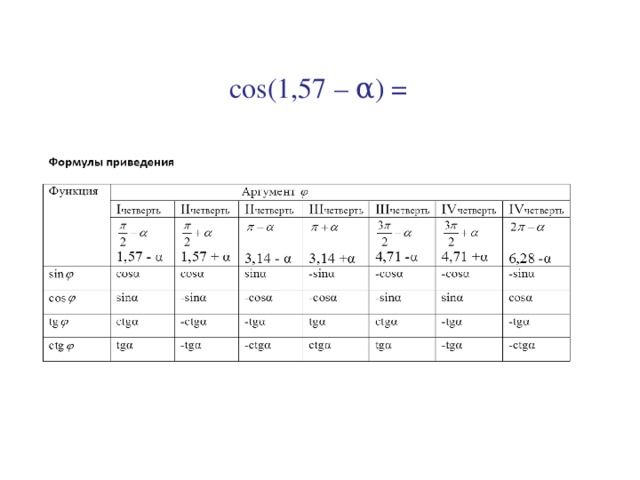
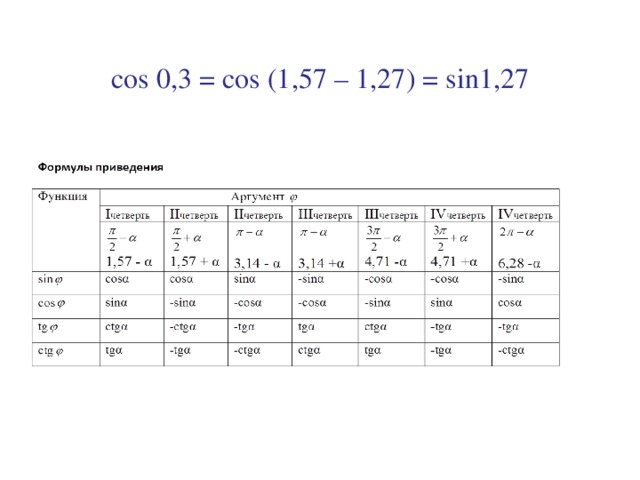
2) cos(1, 57 – α) = sinα
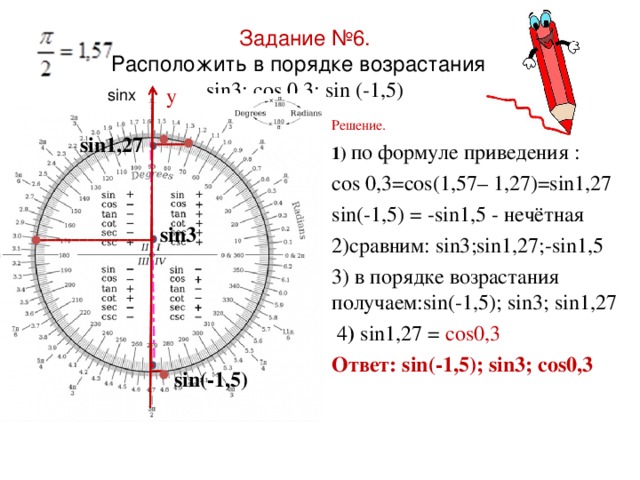
cos 0, 3 = cos (1, 57 – 1, 27) = sin1, 27
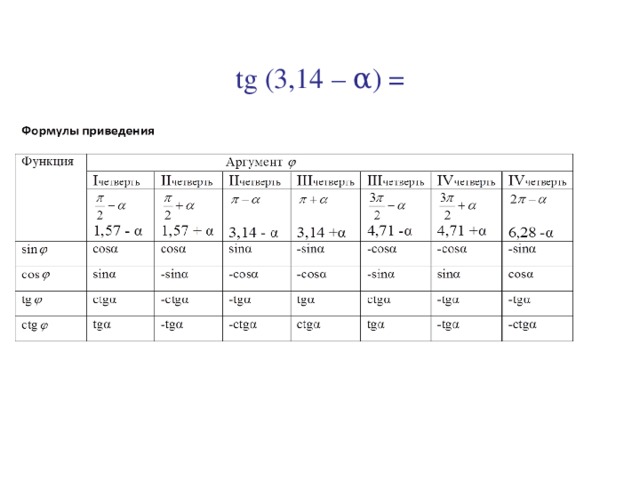
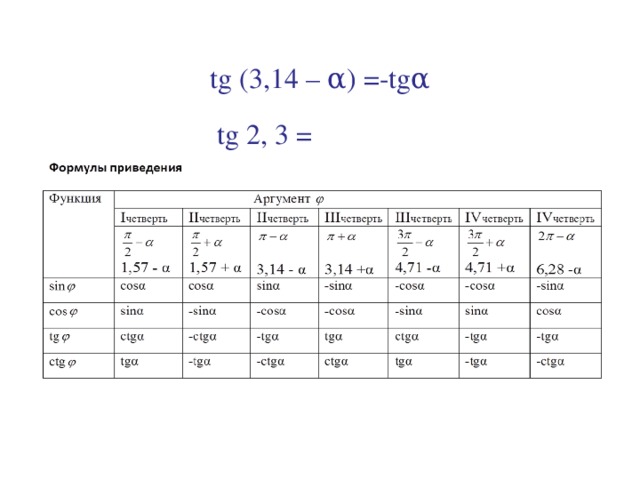
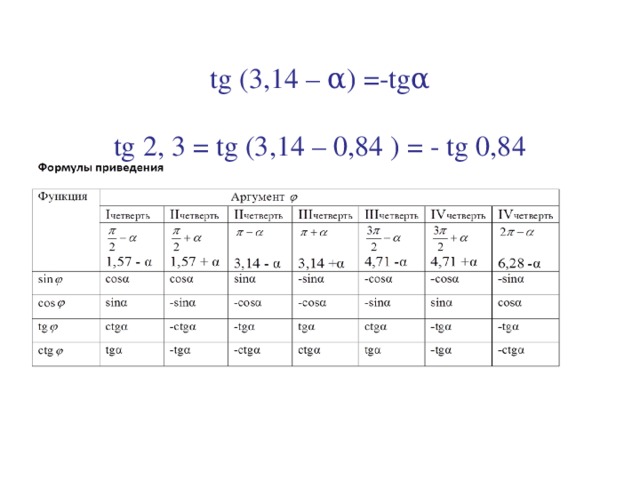
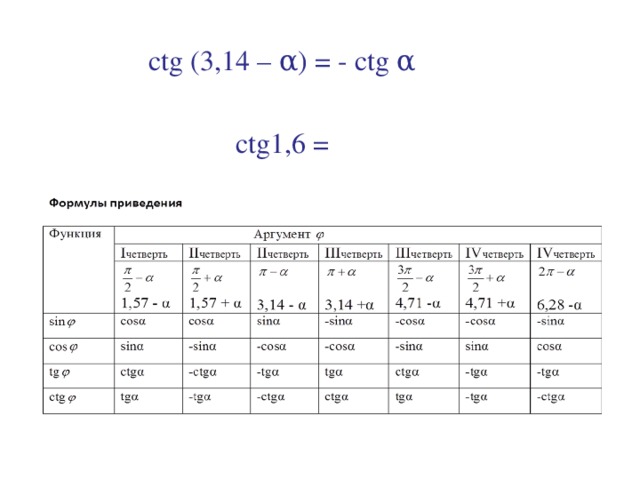
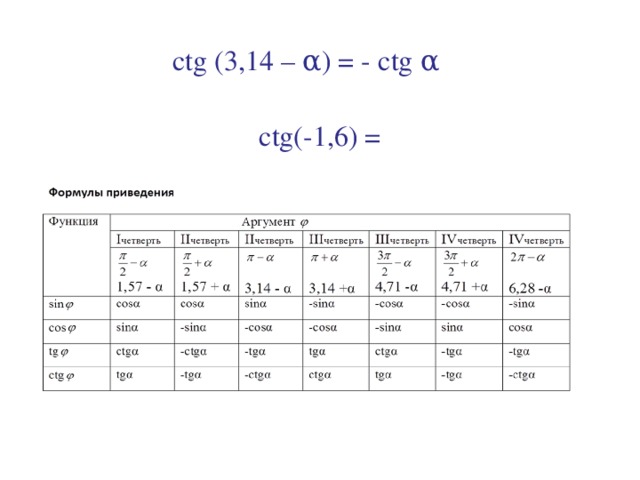
3). tg(3, 14 – α) = - tgα
tg 2, 3 = tg (3, 14 – 0, 84 ) = - tg 0, 84
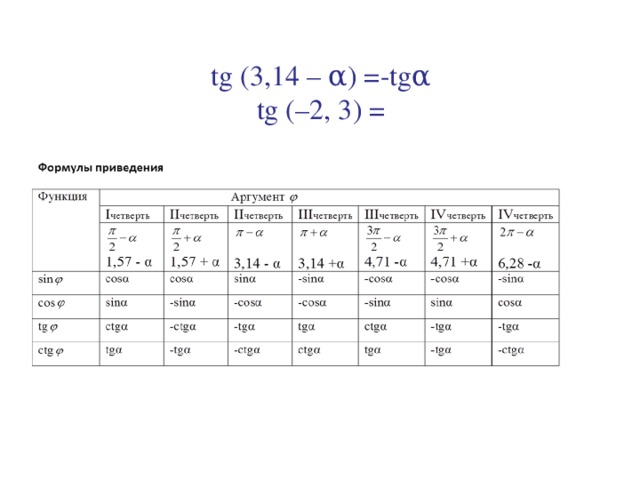
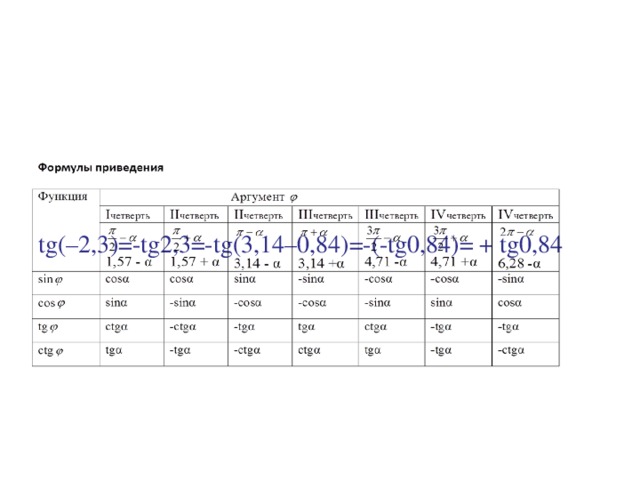
tg(–2, 3)= - tg2, 3= - tg(3, 14–0, 84)= - ( - tg0, 84)= + tg0, 84
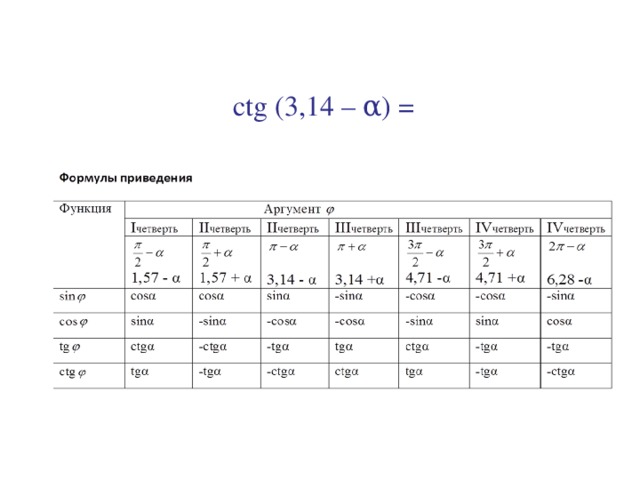
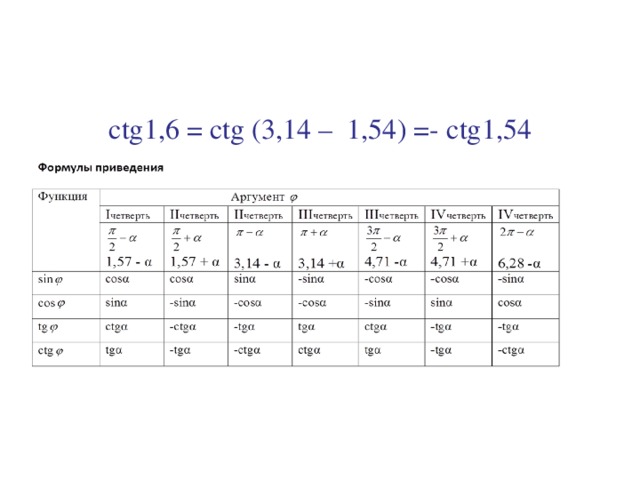
4) сtg (3, 14 – α) = - ctgα
сtg1, 6 = сtg (3, 14 – 1, 54) = - сtg1, 54
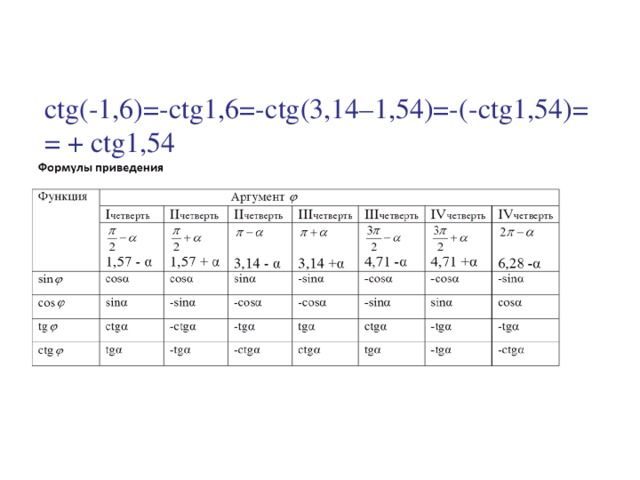
сtg( - 1, 6)= - сtg1, 6= - сtg(3, 14–1, 54)= - ( - сtg1, 54)= + сtg1, 54
Пример 7. Расположите числа в порядке возрастания
tg2, 3; tg( - 2, 3); tg( - 1, 5)
Решение.
При сравнении tg должны выполняться следующие условия:
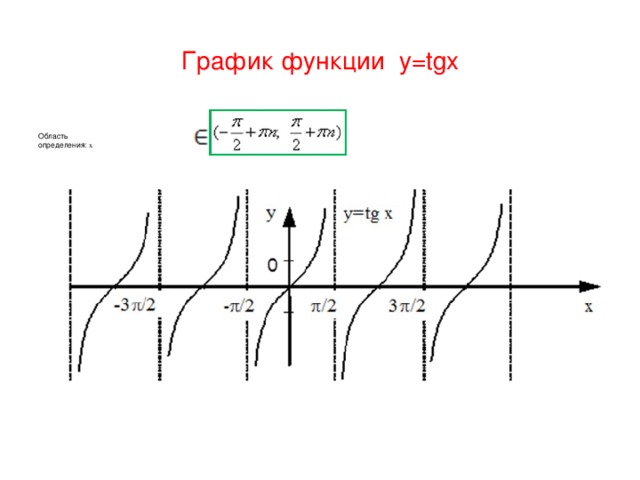
1) х или ( - 1, 57; 1, 57) одному из промежутков области определения, т. к. функция тангенс прерывна ;
1) линия тангенсов параллельна оси у, проводим перпендикуляры на ось у.
По формулам приведения имеем:
tg 2, 3 = tg (3, 14 – 0, 84 ) = - tg 0, 84 ( - 1, 57; 1, 57)
tg( - 2, 3) = - tg 2, 3 = - tg (3, 14 – 0, 84 ) = + tg 0, 84
tg( - 1, 5) = - tg1, 5 ( - 1, 57; 1, 57)
Сравним: - tg 0, 84; tg 0, 84; - tg1, 5.
Ответ: tg( - 1, 5); tg2, 3; tg( - 2, 3)
Пример 8.
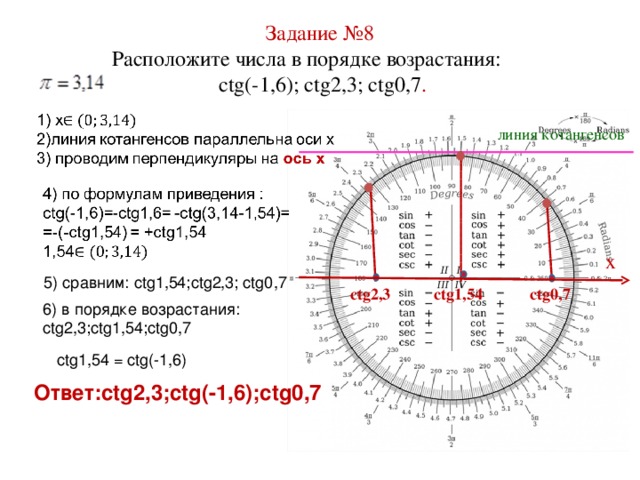
Расположите числа в порядке возрастания: ctg( - 1, 6); ctg2, 3; ctg0, 7
Решение.
При сравнении котангенсов должны выполняться следующие условия:
1)одному из промежутков области определения, т. к. функция котангенс прерывна ;
2). линия котангенсов параллельна оси х, то для нахождения сtg 0, 7 достаточно определить значение y в точке 0, 7 радиан, т. е. проводим перпендикуляры на ось х.
По формулам приведения имеем:
ctg( - 1, 6) = - сtg1, 6 = - сtg (3, 14 – 1, 54) =+ сtg1, 54 1, 54
Сравним: сtg1, 54; ctg2, 3; ctg0, 7
В порядке возрастания: ctg2, 3; сtg1, 54; ctg0, 7 Ответ: ctg2, 3; ctg( - 1, 6); ctg0, 7
Числовая окружность. Тригонометрический круг. Тест.
Задание 1. Запишите максимальное значение ординаты в тригонометрическом круге.
Задание 2. Запишите минимальное значение абсциссы в тригонометрическом круге.
Задание 3. Сколько точек на тригонометрическом круге имеют ординату 0, 5?
Задание 4. Укажите номер четверти, в которую попадает угол 369 градусов
Задание 5. Укажите наименьшее значение синуса любого угла
Задание 6. Укажите максимально возможное значение косинуса угла
Задание 7. Сколько точек на тригонометрическом круге имеют абсциссу, равную 0, 5?
Задание 8. Сколько точек на тригонометрическом круге имеют ординату, равную 1?
Задание 9. Укажите номер квадранта, в котором расположен угол, равный 1000 градусов
Задание 10. Укажите номер четверти, углы которой имеют положительный синус и отрицательный косинус
№ вопроса ответы
1 1
2 - 1
3 2 точки
4 1 четверть
5 - 1
6 1
7 2 точки
8 1 точка
9 4 четверть
10 2 четверть
Задания для самостоятельного закрепления
Расположите в порядке возрастания числа:
a) sin 0, 3, sin 1, 1, sin (—1, 2);
б) sin 4, sin 3, 6, sin 2;
в) sin 0, 4, sin (—0, 9), sin 1, 4;
r) sin 4, 3, sin 2, 9, sin 1, 9.
a) cos 0, 3, cos (—2, 9), cos 1, 8;
б) cos 5, 3, cos 4, 4, cos 6, 2;
в) cos 0, 5, cos (—1, 3), cos 3;
r) cos 6, 1, cos 3, 5, cos 4, 9.
a) tg( —0, 4), tg 1, 2, tg 0, 8;
б) tg2, 8, tg3, 9, tg 1, 6;
в) tg 0, 6, tg(—1, 3), tg( — 0, 7);
r) сtg 4, 3, сtg 1, 7, сtg 2, 5.
Презентация по математике "Тригонометрический круг. Сравнение значений тригонометрических функций. Углы в радианах" (5.68 MB)
1
6550
1117
Нравится
0
