Получите свидетельство
Вход
Синус, косинус и тангенс углов от 0 ⁰ до 180 ⁰
Геометрия 9
Автор:
Сидорова А.В.
МБОУ СОШ № 31
Г. Мурманска
У
- Введём прямоугольную систему координат Оху
и построим полуокружность радиуса 1 с центром в начале координат, расположенную в I и II четверти.
Такую окружность назовём единичной .
h
Обозначим буквой α
угол между лучом h и
1
положительной
полуосью абсцисс .
А(х ;у)
у
-1
1
α
х
О
В
Х
ОА = 1
АВ = у
ОВ = х
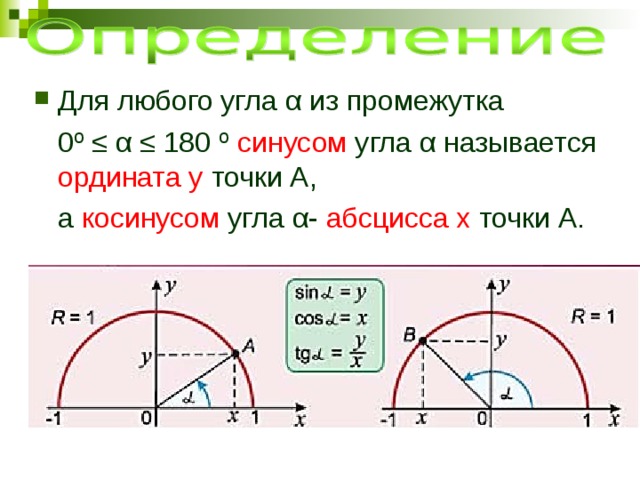
- Для любого угла α из промежутка
0º ≤ α ≤ 180 º синусом угла α называется ордината у точки А,
а косинусом угла α- абсцисса х точки А.
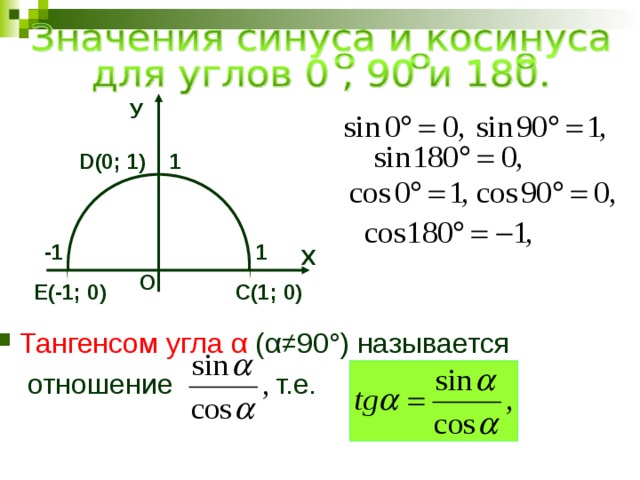
У
D(0; 1)
1
-1
1
Х
О
С(1; 0)
E(-1; 0)
- Тангенсом угла α (α≠90°) называется
отношение т.е.
Уравнение окружности с центром в точке(0; 0) и
радиусом 1:
х 2 + у 2 = 1.
Формулы приведения
sin β = sin (180⁰ - α ) = sin α
cos β = cos (180⁰ - α ) = - cos α
tg β = tg (180⁰ - α ) = - tg α
α
β
α и β - смежные
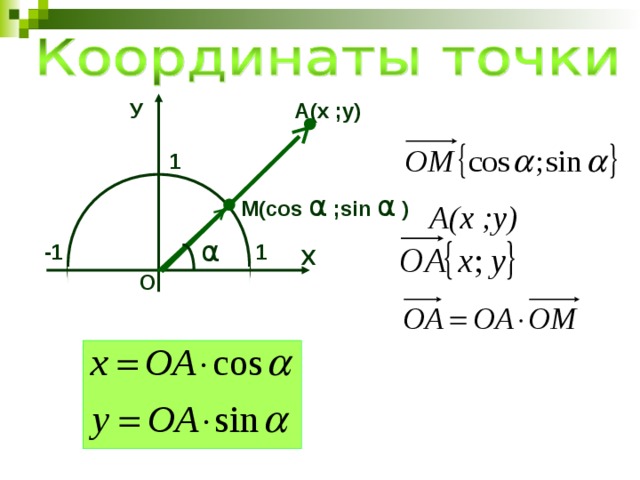
А(х ;у)
У
1
М(cos α ;sin α )
А(х ;у)
α
1
-1
Х
О
Синус, косинус и тангенс углов от 0 до 180 (1000 KB)
0
1463
230
Нравится
0
