Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа» пос Рудный
Кавалеровского муниципального района Приморского края
Конспект урока по математике
в 10 классе
«Решение показательных неравенств»
подготовила
учитель математики
Ильина Эльвира Викторовна
пос Рудный
2017
Урок в 10 классе.
Тема урока: «Решение показательных неравенств».
Цели урока:
образовательные: формирование умений и навыков решать показательные неравенства; формирование заинтересованности учащихся в решении показательных неравенств при подготовке к ЕГЭ.
развивающие: активизация познавательной деятельности; развитие навыков самоконтроля и самооценки, самоанализа своей деятельности.
воспитательные: формирование умений работать самостоятельно; принимать решение и делать выводы; воспитание устремлённости к самообразованию и самосовершенствованию; осознание учащимися социальной практической значимости учебного материала по изучаемой теме.
Тип урока: урок ознакомления с новым материалом. Форма урока: комбинированный урок
Ход урока
I Организационный момент.
Сообщение учителем целей, задач и структуры урока, его основных моментов.
II Проверка домашней работы.
№ 214 (2, 4)
Ответы: 2) х=2 и х=0; 4) х=1
№ 225 (2, 4)
Ответы: 2) х=2 4) х=1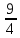 = 3,25
= 3,25
III Работа у доски. Актуализация знаний.
На доске написаны четыре показательных уравнения. Учащимся предложены четыре карточки, на которых изображены символы , , , , соответствующие уравнениям. Каждый учащийся вытаскивает по выбору карточку и начинает решать показательное уравнение.
После решения всех показательных уравнений, выполняется коллективная проверка.
Уравнения:
| ( 5-х = х = - |
х – 3 = 0 х = 3 |
2х – 1 = 0 2х = 1 х = |
(х-1)(х+2) = 0 х-1=0 или х+2=0 х=1 х=-2 |
IV Объяснение нового материала.
Запишем тему урока «Решение показательных неравенств».
Прежде чем начать изучение нового материала, ответьте на вопросы:
Чем неравенство отличается от уравнения? (ответ: знаком)
Что является решением неравенства? (ответ: промежуток)
Определение: Показательное неравенство – это неравенство, содержащее неизвестное в показателе.
Примеры: 2х х+3 22 и т.д.
Делаем подзаголовок «Решение показательных неравенств».
Решение показательных неравенств сводится к решению показательного неравенства ах ав (ах в).
Если а 1, функция у = ах возрастающая, то х в (х
Если 0 функция у = ах убывающая, то х в). Знак меняется на противоположный.
Некоторые показательные неравенства решаются с помощью замены
ах = t и сводятся к квадратным неравенствам (t 0).
Некоторые показательные неравенства решаются графически. Больше та функция, которая расположена выше графика другой функции. Меньше – если расположена ниже графика другой функции.
V Закрепление.
Приобретать знания - храбрость
Приумножать их – мудрость
А умело применять – великое искусство.
Ребята, сейчас мы будем решать показательные неравенства, использую номера из учебника. Открываем учебник и находим № 228 (1, 2, 3, 5).
Первые два примера я решу на доске покажу оформление решения показательных уравнений.
| 1. 3х 9 3х 32 x 2 Чертим числовую прямую и на ней отмечаем 2 и определяем на каком промежутке x 2
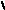     
2
Ответ: (2; ).
| 2. ( ( x Чертим числовую прямую и на ней отмечаем 2 и определяем на каком промежутке x
    
2
Ответ: (-; 2) |
Примеры 3 и 5 учащиеся по желанию выходят к доске и решают.
| 3. ( 2-2х 1 -2x х -

Ответ: (
| 4. 23х 23x 2-1 3x -1
Ответ: [ |
Следующий № 229 (1, 3). Первый пример продолжают решать учащиеся у доски по желанию.
1. 5х-1
5х-1
х-1 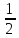
х 1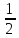




Ответ: (-; ]
Третий пример решаю я на доске, вспоминая с учащимися решение квадратичных неравенств.
3 3х2-4 1
3х2-4 30
х2 – 4 0, парабола, ветви которой направлены вверх.
х2 – 4 = 0
х2 = 4
х1 = 2, х2 = -2





- 2
2
Ответ: (-; -2][2; ).
Следующий № 232 состоит из четырех примеров, решение первого разберем всем коллективно, а остальные решаем в тетрадях самостоятельно и проверяем ответы.
| 3х+2 + 3х-1 Выносим общий множитель за скобку 3х(9 + 3х( Делим обе части неравенства на 3х х
1
Ответ: (-; 1)
| 2х-1 + 2х+3 17 2х( 2х 2
1
Ответ (1; ) |
| 22х-1 + 22х-2 + 22х-3 448 22х( 22х 512 2х 9 х 4,5
4,5
Ответ: [4,5; )
| 53х+1 – 53х-3 624 53х ( 53х 125 3х 3 х 1
1 Ответ: (-; 1]
|
VI Домашнее задание.
№ 228 (4, 6), 229 (2, 4)
VII Итог урока: выставить отметки, оценить работу каждого.
Какие неравенства вы сегодня решали?
Какие методы решения показательных неравенств вы знаете?
Чему вы научились сегодня на уроке?
Пригодятся ли вам в будущем умения решать показательные неравенства?
Чувствовали ли вы себя комфортно на уроке?
Понравился ли вам сегодня урок?
Какую я себе поставил оценку за урок?
Что я знаю очень хорошо?
Что мне надо подучить?
Спасибо за урок!

 Получите свидетельство
Получите свидетельство Вход
Вход


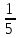 )х =
)х = 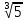
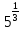
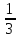
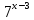 = 1
= 1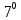
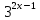 = 1
= 1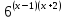 = 1
= 1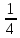









 Решение показательных неравенств (120.79 KB)
Решение показательных неравенств (120.79 KB)
 0
0 470
470 12
12 Нравится
0
Нравится
0


