Государственное автономное образовательное учреждение
среднего профессионального образования
Новосибирской области
«Барабинский медицинский колледж»
Цикловая методическая комиссия общих гуманитарных,
социально-экономических дисциплин
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
комбинированного занятия
для преподавателя
Дисциплина: Математика
Раздел 3 «Алгебра и начала анализа»
Тема 3.12 «Решение показательных уравнений и неравенств»
для специальности 34.02.01 Сестринское дело
по программе базовой подготовки
курс 1
Барабинск, 2015 г
Рассмотрена на заседании
ЦМК ОГСЭД
Протокол № ___________
От ____________ 20___г.
Председатель ЦМК
______________________
(Ф. И. О.)
______________________
(подпись)
Разработчик:
Преподаватель физики 1 квалификационной категории Вашурина Т. В.
Содержание
| Методический лист | 4 |
| Формирование требований ФГОС при изучении темы | 5 |
| Выписка из тематического плана дисциплины «Математика» | 6 |
| Актуальность изучения математики | 7 |
| Примерная хронокарта занятия | 8 |
| Блок информации по теме | 11 |
| План самостоятельной работы студентов | 14 |
| Приложение №1 | 15 |
| Приложение №2 | 16 |
| Приложение №3 | 17 |
| Домашнее задание | 18 |
| Перечень оборудования и оснащения | 18 |
| Список использованных источников | 19 |
Методический лист
Тема 3.12 «Решение показательных уравнений и неравенств»
Вид занятия: комбинированный урок.
Методы обучения: объяснительно-иллюстративный с использованием информационных технологий (ЭОР, мультимедийная презентация), репродуктивный, частично-поисковый, метод дифференцированного обучения.
Уровень усвоения информации: первый (узнавание ранее изученных объектов, свойств) + второй (выполнение деятельности по образцу, инструкции или под руководством)
Образовательные цели: формировать умения решать показательные уравнения и неравенства. Способствовать формированию умения организовывать собственную деятельность, выбирать типовые методы и способы выполнения упражнений, принимать решения в стандартных ситуациях, оценивать их выполнение и качество.
Воспитательные цели: развивать коммуникативные способности; создавать условия для развития скорости восприятия и переработки информации, культуры речи; формировать умение работать в коллективе и команде.
Развивающие цели: способствовать выработке навыков решения задач.
Формирование требований ФГОС при изучении темы
«Решение показательных уравнений и неравенств»
В результате изучения темы обучающийся должен уметь:
Изучение темы 3.12 способствует формированию у обучающихся следующих общих компетенций:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения задач, оценивать их выполнение и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 6. Работать в коллективе и команде.
Выписка из тематического плана
дисциплины «Математика»
специальность «Сестринское дело»
| Тема 3.12 Решение показательных уравнений и неравенств | Содержание учебного материала | 2
|
| Решение показательных, уравнений и неравенств; равносильность уравнений. |
| Лабораторная работа | - |
| Практическое занятие | - |
| Контрольная работа | - |
| Самостоятельная работа обучающихся: - Работа с электронным приложением к учебнику «Алгебра 10-11»; - работа с учебником, выполнение упражнений [2, с.224-230, с.231 упр. 462, 467 (а, б)]; - работа с конспектом лекции. | 1 |
Актуальность изучения математики
В требованиях к результатам освоения основной профессиональной программы ФГОС СПО по специальности «Сестринское дело» сказано, что медицинская сестра должна обладать профессиональными компетенциями, включающими в себя способность самостоятельно оценивать состояние и потребности пациента, вести правильное наблюдение за ним и принимать обоснованные ответственные решения – ведь от его профессиональной компетентности зависит здоровье и жизнь пациента.
Основная профессиональная образовательная программа предусматривает изучение математического и общего естественнонаучного циклов.Значимость математических методов в профессиональной подготовке среднего медицинского персонала очень велика. Наряду с безусловной важностью изучения клинических дисциплин необходимо изучение и прочное усвоение математики. Будущей медицинской сестре необходимо знать метрическую систему единиц для правильного расчета количества таблеток и капсул, объема лекарственного средства для различного вида инъекций, уметь вычислять дозы при парентеральном введении лекарственных средств, скорость внутривенного введения лекарственных средств, а также распознавать ошибки в назначениях врача. Вычислительные ошибки при разведении лекарственных препаратов, которые вводятся больному, могут привести к трагическим последствиям.
В подготовке медицинских сестер выдвигают в качестве основного принципа обучения реализацию межпредметных связей специальных и общепрофессиональных дисциплин. Межпредметные связи по составу показывают, что используется, трансформируется из других дисциплин при изучении конкретной темы. При правильном действии межпредметные связи не только способствуют систематизации учебного процесса и повышению прочности усвоения знаний, но и вызывают усиление познавательного интереса к обучению. В результате знания становятся конкретными и обобщенными, что дает студентам возможность применять их на практике.
Примерная хронокарта занятия по теме «Решение показательных уравнений и неравенств»
(время занятия 90 минут)
| № | Этапы занятия | Деятельность | Цель этапа занятия | Оснащение этапа | Мин. |
| преподавателя | студентов |
| 1 | Орг. момент. | Приветствие. Проверка готовности аудитории. | Дежурный информирует об отсутствующих. Контроль внешнего вида студентов. | Мобилизация внимания, выявление готовности аудитории к занятию. | Журнал группы. | 1 |
| 2 | Актуализация опорных знаний. | Проводит фронтальный опрос группы, анализирует степень усвоения предыдущей темы (без выставления оценки). | Устно отвечают на вопросы | Выявление степени подготовки студентов к занятию и степень усвоения материала по предыдущей теме. Развитие грамотной речи обучающихся. | Вопросы для фронтального опроса группы (Приложение №1) | 10 |
| 3 | Сообщение темы занятия, постановка цели, обозначение актуальности данной темы. | Сообщает тему занятия, определяет цель, обосновывает значимость изучаемой темы. | Слушают, записывают дату и тему занятия в рабочих тетрадях. | Обозначить цель занятия, заинтересовать обучающихся, сконцентрировать их внимание. | Методическая разработка, мультимедийное оборудование, мультимедийная презентация. | 2 |
| 4 | Изучение нового материала по плану. | Объясняет новый материал, сохраняет записи на доске. Демонстрирует презентацию. | Слушают, анализируют, выделяют главное, делают выводы, конспектируют.
| Рассмотреть способы решения простейших показательных уравнений и неравенств. | Учебник Алгебра и начала математического анализа.Под ред. А. Н. Колмогорова, методическая разработка (блок информации), мультимедийное оборудование, мультимедийная презентация, ЭОР с видеофрагментами. | 25 |
| 5 | Первичное закрепление знаний, выполнение упражнений. | Выполняет пошаговую проверку деятельности учащихся, оказывает помощь, консультирует. | Работают в коллективе, выполняя одинаковые задания, аналогичные разобранным при объяснении. (Студенты, выполнившие основное задание, получают индивидуальные карточки с дополнительным заданием) | Закрепление и систематизация материала, ликвидация пробелов в понимании в полученных знаниях. Формирование умения решать показательные уравнения и неравенства. Организация собственной деятельности, выбор типовых методов и способов решения задач, оценка их выполнения. | Методическая разработка, презентация. Приложение №2 (учебник Алгебра и начала математического анализа. под ред. А. Н. Колмогорова: стр.231 №№ 460, 461, 463 (а, б), 466) | 30 |
| 6 | Задание на самостоятельную работу. | Определяет набор заданий для самостоятельной работы, проводит инструктаж по выполнению работы, определяет время самостоятельной работы студентов. | Слушают преподавателя, задают вопросы. Всем даётся один и тот же набор задач, которые можно выполнять, консультируясь только с преподавателем. | Развитие скорости восприятия и переработки информации, пунктуальности. | Слайд презентации с инструкциями, раздаточный материал с заданиями на отдельных листах для самостоятельной работы студентов.
| 2 |
| 7 | С. р. Контроль текущих теоретических и практических знаний, контроль конечного уровня знаний. | Наблюдает за работой учащихся, оказывает помощь, консультирует | Работают индивидуально, используют текст учебника, решают задачи по образцу. | Закрепление материала, формирование умения делать выводы, обобщать. Формирование умения принимать решения. Контроль усвоения знаний и умений учащихся. | Задания в 2-х вариантах для итогового контроля. Приложение №3 | 15 |
| 8 | Итоговый контроль. | Контролирует взаимопроверку (работа в команде), поясняет критерии оценки. | Предоставляют выполненное задание, работают в паре, (работа в малой группе), сопоставляют ответы с эталонами, выставляют оценки. | Закрепление знаний по теме, выявление степени усвоения материала. | Слайд презентации с эталонами ответов и критериями отметки (приложение №3). | 3 |
| 9 | Подведение итогов занятия, выставление оценок. | Оценивает индивидуальную работу, обоснование полученных студентами оценок. | Слушают, задают вопросы, участвуют в обсуждении. | Развитие эмоциональной устойчивости, объективности оценки своих действий, умения работать самостоятельно. | Журнал группы. | 1 |
| 10 | Домашнее задание | Проводит инструктаж по выполнению домашнего задания. | Слушают, записывают, задают вопросы. | Оптимизация самоподготовки, определение объема самостоятельной внеаудиторной работы. | Слайд презентации с домашним заданием. | 1 |
Блок информации
Изложение учебного материала по теме:
«Решение показательных уравнений и неравенств»
Решение показательных уравнений
Определение: Показательным уравнением называется уравнение вида
ах= b, где a 0, a ≠ 1 и уравнения, сводящиеся к этому виду.
Сколько решений может иметь показательное уравнение?
Так как область значений функции у = a - множество положительных чисел, то при b b = 0 – корней нет, при b 0 – один корень.
- множество положительных чисел, то при b b = 0 – корней нет, при b 0 – один корень.
Методы решения показательных уравнений:
а) Метод уравнивания оснований.
б) Метод вынесения общего множителя за скобки.
в) Метод введения вспомогательной переменной
г) Графический метод, метод подбора
Из свойств показательной функции знаем, что ее область значений ограничена положительными вещественными числами. Тогда если b = 0, уравнение не имеет решений. Такая же ситуация имеет место быть, в уравнении где b
Теперь положим, что b0. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0
Исходя из этого и применяя теорему о корне, получим, что уравнение ax = b иметь один единственный корень, при b0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = ac.
Тогда очевидно, что с будет являться решением уравнения ax = ac.
Рассмотрим следующий пример: решить уравнение 5(x2 - 2*x - 1) = 25.
Представим 25 как 52, получим:
5(x2 - 2*x - 1) = 52.
Или что равносильно :
x2 - 2*x - 1 = 2.
Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.
Ответ: 3;-1.
Решим уравнение 4x – 5*2x + 4 = 0. Сделаем замену: t=2x и получим следующее квадратное уравнение:
t2 - 5*t + 4 = 0.
Решаем это уравнение любым из известных способов. Получаем корни t1 = 1
t2 = 4
Теперь решаем уравнения 2x = 1 и 2x = 4.
Ответ: 0;2.
Задание устное:
Для каждого показательного уравнения определите метод решения:
1) 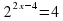 ; 2)
; 2) 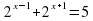 ;
;
3) 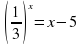 ; 4)
; 4)  ;
;
5) 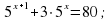 6)
6)  ;
;
7) 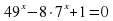 ; 8)
; 8)  .
.
Решение показательных неравенств
Решение простейших показательных неравенств основывается тоже на свойствах возрастания и убывания функции. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0, то данная функция будет убывающей на всем множестве вещественных чисел.
Рассмотрим пример: решить неравенство (0.5)(7 - 3*x)
Заметим, что 4 = (0.5)2. Тогда неравенство примет вид (0.5)(7 - 3*x) (-2). Основание показательной функции 0.5 меньше единицы, следовательно, она убывает. В этом случае надо поменять знак неравенства и не записывать только показатели.
Получим: 7 - 3*x-2.
Отсюда: х
Ответ: х
Если бы в неравенстве основание было больше единицы, то при избавлении от основания, знак неравенства менять было бы не нужно.
План самостоятельной работы студентов
Тема: «Решение показательных уравнений и неравенств»
| № | Название этапа | Описание этапа | Цель | Время |
| 1 | Актуализация опорных знаний. | Повторяют, отвечают устно на вопросы по предыдущей теме. Приложение №1. | Выявление степени усвоения материала по предыдущей теме. | 10 |
| 2 | Первичное закрепление знаний. | Выполняют одинаковые задания, аналогичные разобранным при объяснении. (учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмогорова: стр. .231 №№ 460, 461, 463 (а, б), 466) Приложение№2. (+дополнительные карточки с дифференцированными заданиями) | Закрепление полученных знаний, формирование умений анализировать, сравнивать и обобщать. Формирование навыка решения показательных уравнений и неравенств. | 30 |
| 3 | Контроль конечного уровня знаний. | Выполнение задания для итогового контроля (листы с заданиями для каждого студента) Приложение№3.
| Контроль усвоения знаний и умений учащихся. Выработка умения оценивать конечный результат. Выявление степени достижения цели занятия. | 15 |
Приложение №1
Вопросы для фронтальной беседы по предыдущей теме:
«Показательная функция»
Дайте определение показательной функции.
Ответ: Функцию вида y=ax, где а0, a≠1, х – любое число, называют показательной функцией.
Сформулируйте все известные вам свойства показательной функции.
Ответ:
Область определения показательной функции: D (y)=R – множество всех действительных чисел.
Область значений показательной функции: E (y)=R+ - множество всех положительных чисел.
Показательная функция y=ax возрастает при a1.
Показательная функция y=ax убывает при 0.
Справедливы ли все известные вам свойства степенной функции для показательной функции?
Ответ: Справедливы все свойства степенной функции
а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
а1=а Любое число в первой степени равно самому себе.
ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
(ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают
(a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей.
(a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
а-х=1/ax
(a/b)-x=(b/a)x.
Приложение №2
Задания для первичного закрепления материала
№№ 460, 461, 463 (а, б), 466.
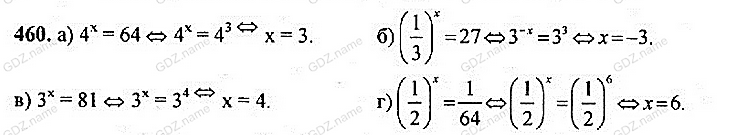
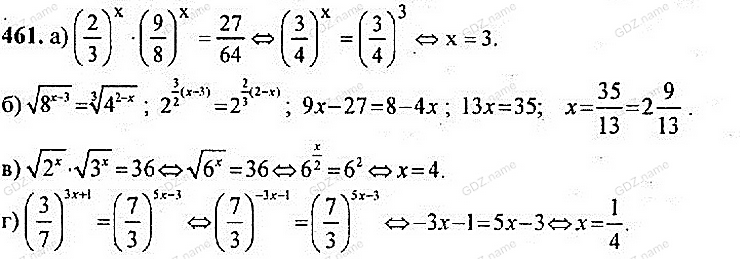
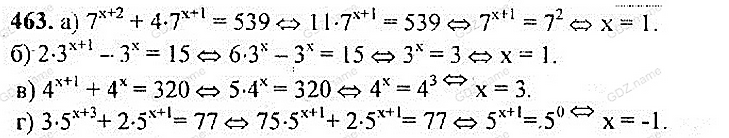
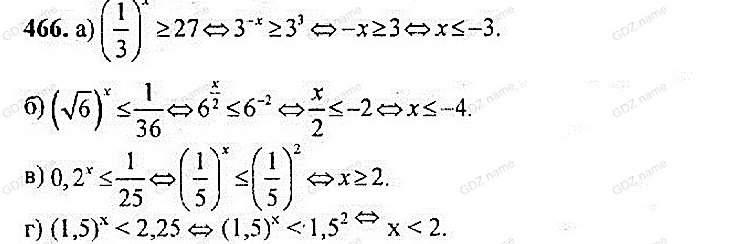
Приложение №3
Задания для самостоятельной работы (итоговый контроль)
Критерии оценки: «5» баллов – 4 верно выполненных задания
«4» балла – 3 верно выполненных задания
«3» балла – 2 верно выполненных задания
Эталоны ответов:
| Вариант | 1 | 2 | 3 |
| I | а | в | 7/6 |
| II | г | б | -5 |
Домашнее задание
Цель: Определить объем информации для самостоятельной работы, обратить внимание на значимые моменты.
Учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмогорова, 10-11 классы: с. 224-230, с.231 упр. 462, 467 (а, б). Работа с электронным приложением к учебнику «Алгебра 10-11», работа с конспектом лекции.
Перечень оборудования и оснащения
1. Доска
2. Компьютерное и мультимедийное оборудование
3. Учебник с заданиями для первичного закрепления знаний, раздаточный материал с заданиями итогового контроля, дополнительные дифференцированные задания по теме (карточки в 2-х вариантах)
4. Электронное учебное пособие (приложение к учебнику)
5. Мультимедийная презентация (22 слайда)
Список использованных источников
Основные источники:
1. Алгебра и начала анализа. 10-11 классы [Текст]: учебник для общеобразовательных учреждений с приложением на электронном носителе: /[А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.].под ред. А. Н. Колмагорова.-20-е изд. - М. : Просвещение, 2011. – 384 с.
2. Социальная сеть работников образования/ Урок по теме «Показательные уравнения и неравенства» [Электронный ресурс] // Режим доступа: http://nsportal.ru/shkola/algebra/library/2013/10/13/urok-po-teme-reshenie-pokazatelnykh-uravneniy-i-neravenstv-11
Дополнительные источники:
1. Электронное учебное пособие (приложение к учебникуАлгебра и начала анализа. 10-11 классы под ред. А. Н. Колмогорова)

Карточка №1
№ 1. Укажите промежуток, которому принадлежит корень уравнения 3х+2+3х+1+3х=39.
А) [-2; 0]
Б) [2; 4]
В) (4; 9]
Г) (0; 2)
№ 2. Решить неравенство: 32x-1272 .
А) (1,5; +&)
Б) (-&; 1,5)
В) (-&; 3,5)
Г) (3,5; +&)
№ 3. Решить уравнение: 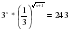
 Карточка № 2
Карточка № 2
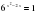
№ 1. Найдите сумму корней уравнения:
А) -2
Б) 0
В) 1
Г) 2
№ 2. Решите неравенство: 
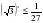
А) (-; -6]
Б) (-; -12]
В) [-6; +)
Г) (-; -1.5)
№ 3. Решите уравнение: 9х-3х-6=0
А) 1
Б) 3 и -2
В) -2
Г) 1/3
Задания для самостоятельной работы (итоговый контроль) 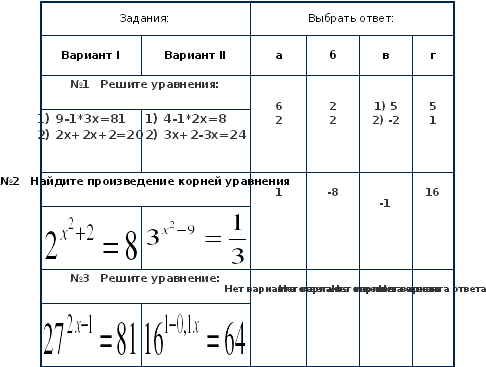
Критерии оценки: «5» баллов – 4 верно выполненных задания
«4» балла – 3 верно выполненных задания
«3» балла – 2 верно выполненных задания
11

 Получите свидетельство
Получите свидетельство Вход
Вход



 - множество положительных чисел, то при b b = 0 – корней нет, при b 0 – один корень.
- множество положительных чисел, то при b b = 0 – корней нет, при b 0 – один корень.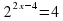 ; 2)
; 2) 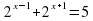 ;
;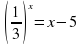 ; 4)
; 4)  ;
;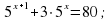 6)
6)  ;
;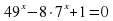 ; 8)
; 8)  .
.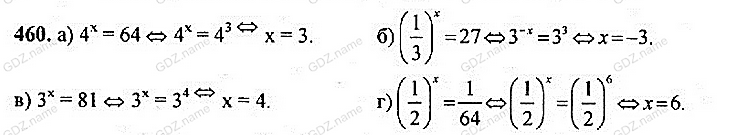
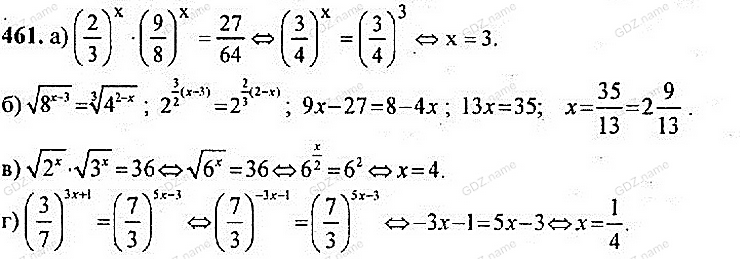
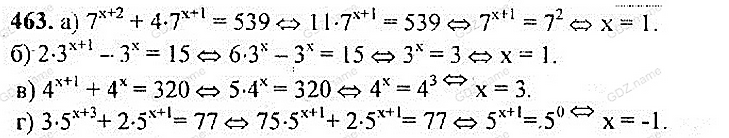
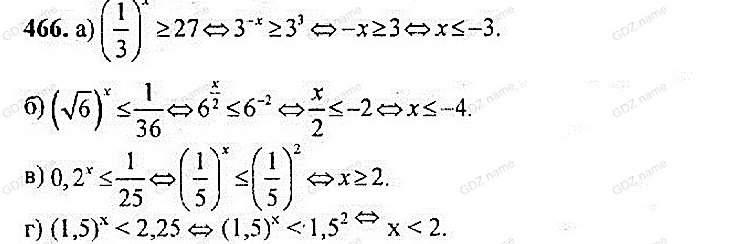


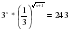
 Карточка № 2
Карточка № 2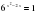

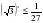










 Методическая разработка занятия по математике "Решение показательных уравнений и неравенств" (для специальности «Сестринское дело») (0.5 MB)
Методическая разработка занятия по математике "Решение показательных уравнений и неравенств" (для специальности «Сестринское дело») (0.5 MB)
 0
0 912
912 114
114 Нравится
0
Нравится
0


