Урок математики по теме: «Решение уравнений разных видов».
Надежда Викторовна Даскина, учитель математики.
Краткая аннотация урока:
Учебный предмет: алгебра и начала анализа.
Уровень образования школьников: 12 класс вечерней (сменной) общеобразовательной школы.
Раздел программы: Уравнения и неравенства. Системы уравнений и неравенств.
Место урока в изучении раздела: заключительный урок.
Тип урока: повторительно-обобщающий.
Форма проведения: традиционный урок.
Формы организации работы учащихся: индивидуальная и групповая.
Цель урока: Обобщение знаний учащихся об уравнениях и способах их решения в соответствии с требованиями выпускных экзаменов.
Задачи урока:
1. Научить использовать кластерную технологию для систематизации знаний;
2. Развивать учебно-познавательные, коммуникативные компетенции;
3. Воспитывать толерантность к чужому мнению.
Ход урока:
1 этап урока .Организационный.
Вступительное слово учителя. Мотивация необходимости повторения темы «Решение уравнений различных видов, способов их решения».
Начнем урок с «рассуждалок». Надеюсь, ребята, вы быстро поймете о чем пойдет речь на уроке. Итак:
-это такая штука, в которой что-то не знаешь, а потом вдруг узнаешь;
-не знаю, есть ли у него листья и стебли, но корни у него есть. Может один, а может больше. И только у некоторых нет и корней;
-иногда задачи решаются только с его помощью. Я не люблю их решать, потому что плохо умею это;
-в 7 классе они линейные, в 8-ом они квадратные, в 10-ом тригонометрические, а в 11-ом показательные и логарифмические.
Вопрос: вы догадались, о чем эти «рассуждалки»? Какие виды уравнений вы знаете? Различаются ли методы решения уравнений? Какой основной способ решения уравнений вы знаете?
2 этап урока. Актуализация опорных знаний.
Работа в группах. Составление кластера по теме урока. (приложение 1).
3 этап урока. Закрепление.
Задание 1. Провести классификацию уравнений по виду, используя составленный кластер. (приложение 2)
Задание 2. Разделить уравнения из приложения 2 на две группы: трансцендентные и алгебраические.
Трансцендентное уравнение, уравнение, содержащее трансцендентные функции (показательные, логарифмические, тригонометрические и обратные тригонометрические) от неизвестного (переменного).
Трансцендентный - лежащий за пределами опыта, недоступный познанию, непостижимый для разума (в идеалистической философии).
Не могущий быть вычисленным алгебраическим путем или выраженным алгебраически (в математике).
Значение слова Трансцендентный по Ожегову:
Трансцендентный - находящийся за пределами мира.
Задание 3. Комментированное решение иррационального, показательного, логарифмического уравнений.
Задание 4. Самостоятельное решение уравнений с последующей самопроверкой по ответам, данным учителем (приложение 3).
4 этап урока. Рефлексия. Заполни таблицу:
|
| Да | Нет | Не совсем |
| 1. Сегодня я узнал, как определить вид уравнения |
|
|
|
| 2. Я понял, как решать уравнение -иррациональное -показательное -логарифмическое |
|
|
|
| 3. Теперь я смогу решить на экзамене задание типа В5 |
|
|
|
| 4. Сегодня на уроке мне было -интересно -трудно |
|
|
|
Домашнее задание. Решить уравнения из приложения 3, которые не решили на уроке.
Приложение№1. Алгоритм составления кластера по теме урока
Учитель задаёт вопросы для определения и группировки элементов будущего кластера. Ответы каждая группа учащихся записывает на заранее подготовленных листах.
1.Какие виды уравнений Вы знаете?
2. Запишите общий вид каждого из названных уравнений.
3. Запишите формулы для нахождения корней каждого из уравнений.
4. Какую «полезную» информацию нужно помнить при решении каждого из этих
уравнений.
Примерный кластер (расположение элементов может варьироваться):











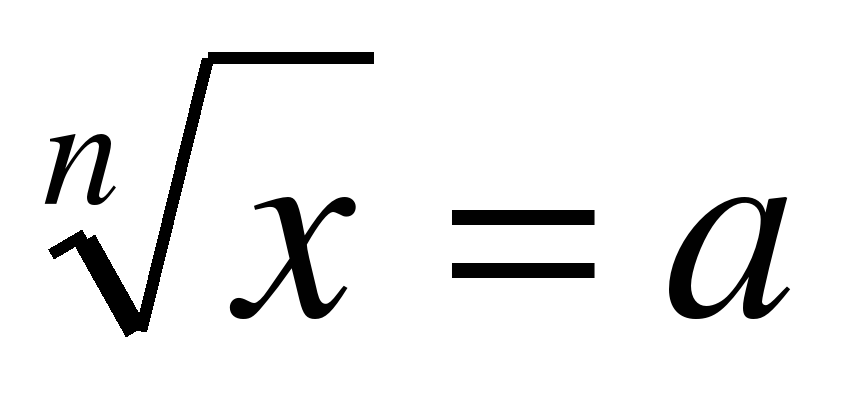
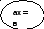
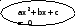
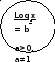
|
| 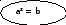   
| 
|
|  | 
|
| Х= a≠0 в-любое | D=b2-4ac X1= X2=
| x=an | x=logab а0 a≠1
| x=ab a0, a≠1
| x=(-1)nargsina+πn, nϵZ x=argcosa+2πn, nϵZ
|
|
| | Полезная» информация: Для линейного уравнения, если а=0, то уравнение корней не имеет. Например, 0х=7. Либо х- любое число. Например, 0х=0. Для квадратного уравнения: если  , то уравнение имеет два различных действительных корня; , то уравнение имеет два различных действительных корня; если  , то уравнение имеет один действительный корень кратности 2; , то уравнение имеет один действительный корень кратности 2; если  , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня: , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
3. Для иррационального уравнения: Одним из самых простых приемов решения иррациональных уравнений является метод освобождения от радикалов путем последовательного возведения обеих частей уравнения в соответствующую натуральную степень. При этом следует иметь в виду, что при возведении обеих частей уравнения в нечетную степень полученное уравнение, эквивалентное исходному, а при возведении обеих частей уравнения в четную степень полученное уравнение будет, вообще говоря, неэквивалентным исходному уравнению, при этом могут появиться «лишние» корни.
4. Для показательного уравнения: Одним из самых простых приёмов решения показательных уравнений является метод сведения обеих частей уравнения к одному основанию.
5. Для логарифмических уравнений: Одним из самых простых приёмов решения логарифмических уравнений является использование определения логарифма. |
|
|
|
|
Приложение 2. Определите вид уравнения, заполните таблицу:
| Вид уравнения | № уравнения |
| Линейное уравнение |
|
| Квадратное уравнение |
|
| Иррациональное уравнение |
|
| Показательное уравнение |
|
| Логарифмическое уравнение |
|
| Тригонометрическое уравнение |
|
1. log(14-x)=-2
2.
3. =4
4. 2x2-13x+15=0
5.
6. cos
7. -5x = 3
8. =11
9. 3x2+4x- 207 = 0 ОТВЕТЫ К ТАБЛИЦЕ:
| Вид уравнения | № уравнения |
| Линейное уравнение | 5;7 |
| Квадратное уравнение | 4;9;15 |
| Иррациональное уравнение | 3;8;12 |
| Показательное уравнение | 2;10;14;16 |
| Логарифмическое уравнение | 1;11;13 |
| Тригонометрическое уравнение | 6 |
10. 9
x-24 = 729
11. log5(2x+8) = -1
12. =
13. log15(3x-9) = log15(x-17)
14. 52x-4 =
15. x2 = 36x
16.
Приложение №3
1. log (x+7)= -2 2. = 5 3.
4. log7(x-6) = 2 5. 6. 54-x=25
7. log5(x-4)=2 8. 9.
10. log3(2x-1)=2 11. 12. 7x-2=49
13. log5(3x+1)=2 14. 15.
16. log5(x+1)=log5(4x-5) 17. 18. 32-2x=81
ОТВЕТЫ:
| ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ | ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ | ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ |
| 1. 42 | 2. 5 | 3. 8 |
| 4. 55 | 5. -8 | 6. 2 |
| 7. 29 | 8. -1 | 9. 4 |
| 10. 5 | 11. 6;-6 | 12. 4 |
| 13. 8 | 14. -18 | 15. 3 |
| 16. 2 | 17. НЕТ РЕШЕНИЙ | 18. -1 |

 Получите свидетельство
Получите свидетельство Вход
Вход














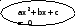
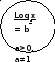
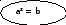









 Разработка урока по математике "Решение уравнений разных видов" (0.13 MB)
Разработка урока по математике "Решение уравнений разных видов" (0.13 MB)
 0
0 604
604 32
32 Нравится
0
Нравится
0









