Елюбаева Гайша Ищановна
учитель математики
Государственное учреждение
«Айдабульская средняя школа»
село Айдабул Зерендинского района
Акмолинской области республики Казахстан
математика
Разноуровневые задания по математике.
Возраст учащихся-16-17 лет
Разноуровневые задания по математике.
Одной из важных задач учителя является формирование у учащихся умений делать выбор, принимать самостоятельное решение. «Я есть мой выбор», - утверждал известный французский философ и писатель Жаль- Поль Сартр. Без выбора невозможно развитие индивидуальности человека. Ребенок должен обладать правами и возможностями в выборе уровня освоения образовательной программы, темпа учебной деятельности,заданий на уроке и способов их выполнения . Проверочная работа должна быть посильной для всех учащихся без исключения, поэтому на уроках математики использую разноуровневые задания, которые позволяют определить уровень знаний, умений, отработать пробелы, тем самым качественно подготовиться к сдаче ЕНТ. Каждому предоставляется возможность рискнуть и попытаться решить более сложную задачу. Ученик учится рисковать и рассчитывать свои силы. Воспитательное значение этого неоспоримо . В классе создается атмосфера психологической поддержки, комфорта.
Тема: Тригонометрия.
Уровень А.
1.Найдите числовое значение выражения 3sin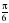
A) 2,5
B) -0,5+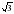
C) 6,5
D) 1
E) 1,5
2.Упростите: 1 + 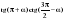
A) 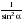
B) 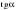
C) 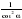
D) 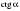
E) 
3.Вычислите: 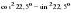
A) 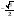
B) 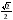
C) -1
D) 1
E) 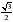
Уровень В
1.Вычислите: 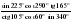
A) 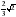
B) 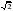
C) 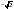
D) 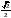
E) 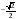
2. Вычислите: 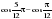
A) 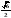
B) 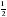
C) 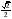
D) 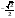
E) 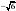
3.Найдите множество значений функции у = 3 + 2sin2 3x
A) (0; 5)
B) (0; 3)
C) [3; 5]
D) (-5; 0)
E) [-5; 5)
| УровеньС.
Найдите 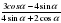 если если  |
|
|
| А) -2 В) -0,2 С) 0,3 Д) 1 Е) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Производная.
Уровень А
1.Найдите производную функции у = х3 + 4х – 5
A) 3х2 + 4х – 5
B) х2 + 4
C) 3х2 + 4
D) 
E) 2х2 + 1
2.Найдите производную функции f(x) = (x4 – 1)(x4 + 1)
A) 12x9
B) x4 - 1
C) 5x5
D) 7x8
E) 8x7
Уровень В.
1. Дано f(x) = (5 + 6x)10. Найдите  (-1)
(-1)
A) -10
B) 10
C) -60
D) 6
E) 60
2. Найдите производную функции у = 
A) 
B) 
C) 
D) 
E) 
3.Дана функция f(x) =  Найдите
Найдите 
A) 
B) 
C) 
D) 
E) 
4.Найдите производную функции: f(x) = 
A) 
B) 
C) 
D) 
E) 
Уровень С.
Найти производную функции h(х)=f(g(х)), если f(х)=sin3х, g(х)= 2-3х.
А) -9 sin2(2-3х) cos(2-3х).
В) sin2(2-3х)cos(2-3х).
С) -9 sin2(2-3х)
Д). -9 cos(2-3х).
Е)10) -9 sin2(2-5х ) cos(-3х).
Тема: Тригонометрические уравнения.
Уровень А.
1.Решите уравнение: 
A) 
B) 
C) Нет решений
D) 
E) 
2.Решите уравнение: sin x = -1
A) 
B) 
C) 
D) 
E) 
3.Решите уравнение: 
A) 
B) 
C) 
D) 
Уровень В.
1.Решите уравнение 3 – 4cos2 x = 0. Найдите сумму его корней, принадлежащих промежутку [0; 3 ]
]
A) 9
B) 7,5
C) 5
D) 6
E) 4
2.Решите уравнение: 
A) (-1)n
B) 
C) 
D) 
E) 
Уровень С.
Решите уравнение 4cos2х-1=0
-
А) п\8+пк\4, к€Z
В) п\4+пк\4,к €Z
С )п\3+пк\4,к €Z
Д) п\6+пк\4,к €Z
Е) ± +пк,к€z
+пк,к€z
2. решить уравнение 
А) 
В) п\2-аrcsin1\5+2пк,к €Z
С) п\2-аrcsin2\5+пк, к€Z
Д) п-аrcsin3\5+5пк, к€Z
Е) п\6-аrcsin3\5+пк, к€Z
Ответы
Тема: Тригонометрия
Уровень А
1)е,2)с,3)в
Уровень В
1)в, 2)д, 3)с
Уровень С
Найдите 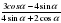 , если
, если  .
.
Решение.
Тема: Производная.
Уровень А
1)с,2)е
Уровень В
1)с,2)а,3)в,4)д
Уровень С.  = 3 ( -3) sin2(2-3х)cos(2-3х) = -9 sin2(2-3х)cos(2-3х).
= 3 ( -3) sin2(2-3х)cos(2-3х) = -9 sin2(2-3х)cos(2-3х).
Тема: Тригонометрические уравнения.
Уровень А
1)а,2)е,3)в
Уровень В
1)с,2)а
Уровень С
1)Решите уравнение 4cos2х-1=0
Решение. Используем формулу
понижения степени:
cos2х = 
4 -1=0
-1=0
cos 2x = −½
Решая полученное уравнение, находим:
2x = ±2π/ 3 + 2πк (к ∈ Z).
х= ± +пк,к€z
+пк,к€z
.
2)Решить уравнение  .
.
Решение:
Использованная литература
Учебная программа для 10-11 классов естественно-математического направления общеобразовательной школы. Астана. 2013. Чакликова С.Е. Алдибаева Т.А. и др.
Степанов Е.Н. Личностно-ориентированный подход в работе педагога. Москва. Сфера. 2004.
Сарсекеев А.С.Тестовые задания по математике. Астана. РНПЦ « Дарын», 2003.
Рустюмова И.П. Пособие для подготовки к ЕНТ. Алматы. 2004.
Алгебра и начала анализа. Учебник для 11 класса. Абылкасымова А, Бекбоев И, Алматы, Мектеп, 2011.
Алгебра и начала анализа. Учебник для 10 класса. Абылкасымова А, Шыныбеков К. Алматы, Мектеп, 2010.
Егоркина Н.В. Математика для поступающих в вузы. Кокшетау. Келешек. 2011.
Сборники тестов за последние 5 лет.


 Получите свидетельство
Получите свидетельство Вход
Вход


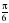
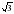
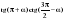
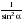
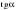
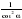
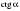

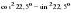
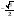
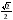
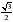
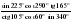
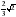
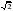
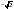
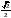
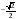
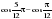
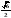
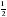
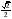
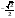
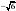
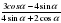 если
если 








 Разноуровневые задания по математике (0.13 MB)
Разноуровневые задания по математике (0.13 MB)
 0
0 1960
1960 388
388 Нравится
0
Нравится
0






