Рабочая программа по алгебре для 8 класса (углубленное изучение)

Пояснительная записка

Рабочая программа по алгебре составлена на основе федерального компонента государственного стандарта общего образования, примерной программы по математике основного общего образования.

Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Алгебра нацелена на формирование математического аппарата для решения задач из математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др. ).

В задачи обучения математики входит:

овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;

овладение навыками дедуктивных рассуждений;

интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;

формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т. д. );

воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;

развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.

Формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.

Методической особенностью курса является расширение традиционных учебных тем за счет теоретико - множественной, вероятностно - статистической и историко - культурной линий. Обращение к теоретико - множественному подходу в изложении некоторых вопросов связано не только с программой изучения математики на профильном уровне, но и удобством такого подхода при введении, например, функции как соответствия между множествами, равносильности уравнений. Специфической особенностью линии является введение в обязательные тексты исторического материала, а в практическую часть - задач из прошлого. Это позволит обращать внимание школьнков на общекультурное значение математики.

Учебно - тематический план

Весь материал – смотрите документ.

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №1

(с углубленным изучением отдельных предметов)»

Рассмотрена Утверждена

на заседании МО приказом директора

протокол № ___ школы

от _____________ от __________ № ___

Рекомендована к утверждению

методическим советом

протокол № ___

от _____________

Рабочая программа

по алгебре

для 8 класса (углубленный курс)

Пояснительная записка

Рабочая программа по алгебре составлена на основе федерального компонента государственного стандарта общего образования, примерной программы по математике основного общего образования.

Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Алгебра нацелена на формирование математического аппарата для решения задач из математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.).

В задачи обучения математики входит:

• овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;

• овладение навыками дедуктивных рассуждений;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);

• воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;

• развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.

• Формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.

Методической особенностью курса является расширение традиционных учебных тем за счет теоретико-множественной, вероятностно-статистической и историко-культурной линий. Обращение к теоретико-множественному подходу в изложении некоторых вопросов связано не только с программой изучения математики на профильном уровне, но и удобством такого подхода при введении, например, функции как соответствия между множествами, равносильности уравнений. Специфической особенностью линии является введение в обязательные тексты исторического материала, а в практическую часть - задач из прошлого. Это позволит обращать внимание школьнков на общекультурное значение математики.

Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. В курсе алгебры 8-го класса продолжается применение формул сокращенного умножения в преобразованиях дробных выражений. Главное место занимают алгоритмы действий с дробями. Формируются понятия иррационального числа на множестве действительных чисел, арифметического квадратного корня. Особое внимание уделяется преобразованиям выражений, содержащих квадратные корни. Даются первые знания по решению уравнений вида 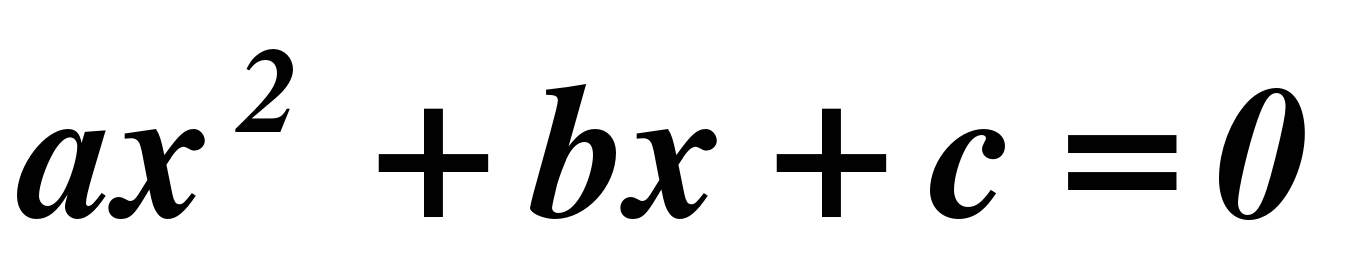, где 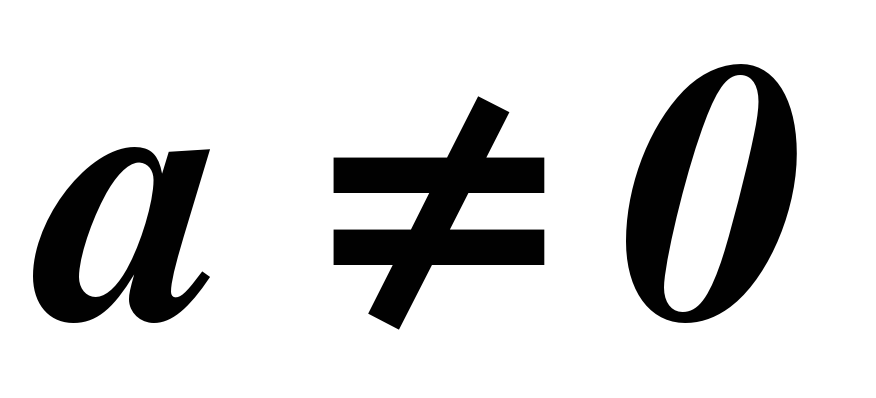, по формуле корней, что позволяет существенно расширить аппарат уравнений, используемый для решения текстовых задач. Продолжается изучение числовых неравенств, на которых основано решение линейных неравенств с одной переменной. Вводится понятие о числовых промежутках. Изучаются свойства функций 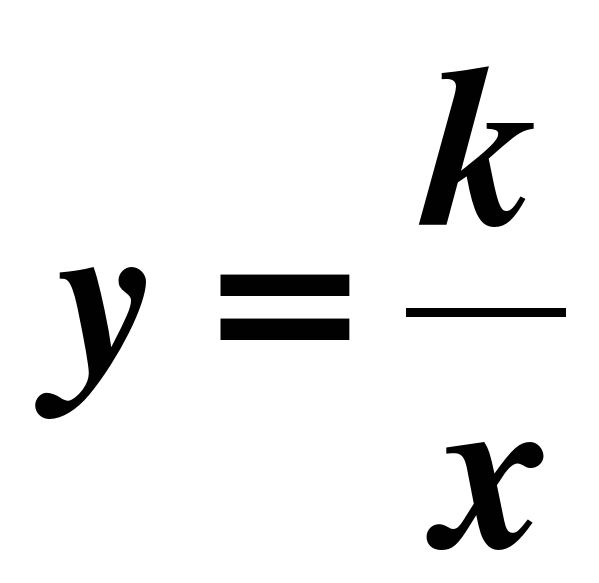, при и , и 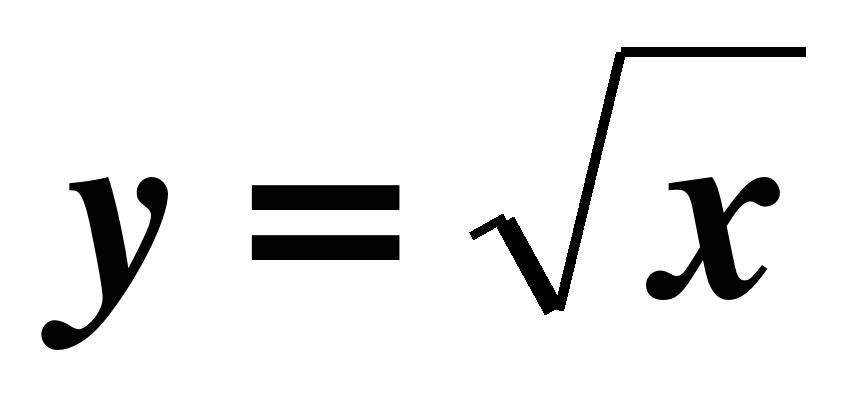. Выявляется связь функции 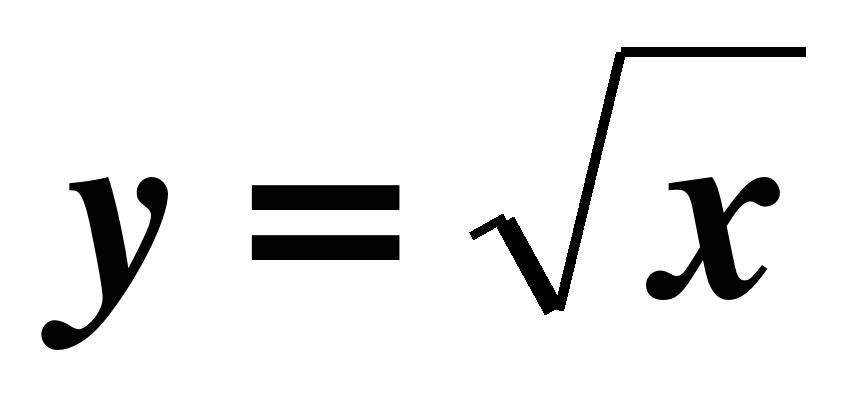с функцией 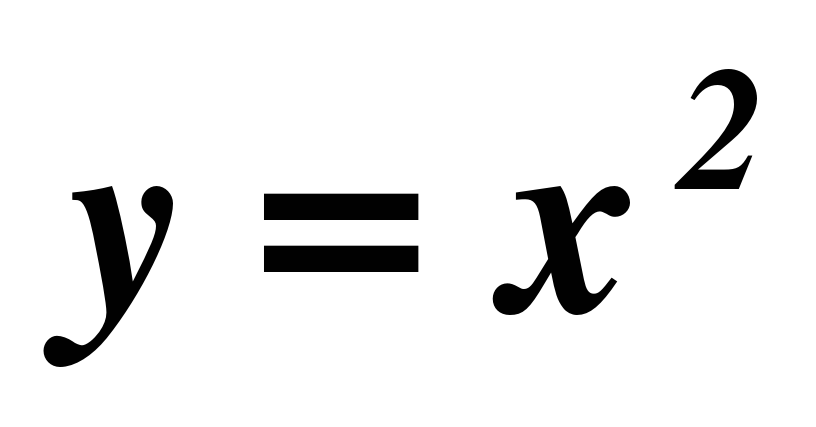, где 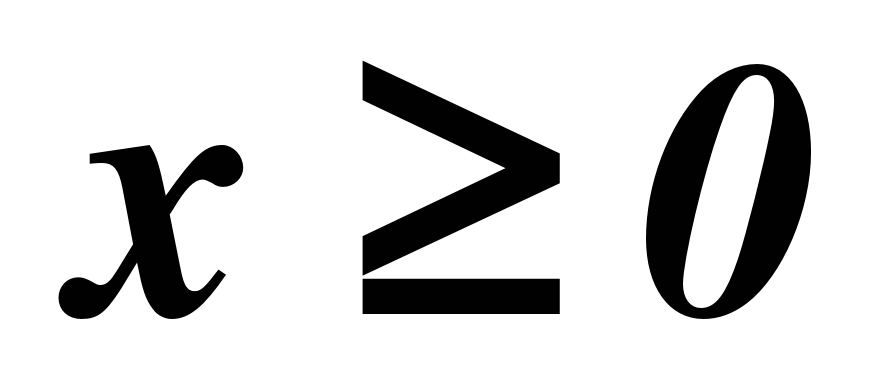. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.

Для более широкого знакомства с математикой введен курс «Элементы статистики и теории вероятностей» в количестве 5 часов. На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Дается классическое определение вероятности, формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения вероятностей.

Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.

На углубленное изучение алгебры программой отводится 175 часов в год.

При изучении предмета используется блочно-модульная технология.

Содержание учебного материала «Алгебра 8»

8 класс (углубленный курс) по УМК Ю.Н. Макарычев и др.

ГЛАВА I. ДРОБИ (23ч.)

РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА.

Рациональные выражения. Основное свойство дроби. Сокращения дробей.

СУММА И РАЗНОСТЬ ДРОБЕЙ.

Сложение и вычитание дробей с одинаковыми знаменателями. Сложение и вычитание дробей с разными знаменателями.

ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ.

Умножение дробей. Возведение дроби в степень. Деление дробей. Преобразование рациональных выражений.

ГЛАВА II. ЦЕЛЫЕ ЧИСЛА. ДЕЛИМОСТЬ ЧИСЕЛ. (19ч.)

МНОЖЕСТВО НАТУРАЛЬНЫХ И ЦЕЛЫХ ЧИСЕЛ

Пересечение и объединение множеств. Взаимно однозначное соответствие. Натуральные числа. Целые числа.

ДЕЛИМОСТЬ ЧИСЕЛ

Свойства делимости. Делимость суммы и произведения. Деление с остатком. Признаки делимости. Простые и составные числа.

ГЛАВА III. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КВАДРАТНЫЙ КОРЕНЬ (29ч.)

МНОЖЕСТВО РАЦИОНАЛЬНЫХ И МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ

Рациональные числа. Действительные числа. Числовые промежутки. Интервальный ряд данных. Абсолютная и относительная погрешность.

АРИФМЕТИЧЕСКИЙ КВАДРАТНЫЙ КОРЕНЬ. ФУНКЦИЯ у=√х

Арифметический квадратный корень. Вычисление и оценка значений квадратных корней. Функция у=√х

СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ

Квадратный корень из произведения, дроби, степени. Преобразование выражений, содержащих квадратные корни. Преобразование двойных радикалов.

ГЛАВА IV. КВАДРАТНЫЕ УРАВНЕНИЯ (32ч)

КВАДРАТНЫЕ УРАВНЕНИЯ И ЕГО КОРНИ

Определение квадратного уравнения. Неполные квадратные уравнения. Формулы корней квадратного уравнения. Уравнения, сводящиеся к квадратным. Решение задач с помощью квадратных уравнений.

СВОЙСТВА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ

Теорема Виета. Выражения, симметрические относительно корней квадратного уравнения. Разложение квадратного трехчлена.

ДРОБНО - РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ

Решение дробно-рациональных уравнений. Решение задач.

ГЛАВА V. НЕРАВЕНСТВА (21ч)

ЧИСЛОВЫЕ НЕРАВЕНСТВА И НЕРАВЕНСТВА С ПЕРЕМЕННЫМИ.

Сравнение чисел. Свойства числовых неравенств. Оценка значений выражений. Доказательство неравенств.

РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ

Решение неравенств с одной переменной. Решение систем неравенств с одной переменной. Решение простейших неравенств с модулем.

ГЛАВА VI. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ (12ч)

СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА.

Определение степени с целым отрицательным показателем. Свойства степени с целым показателем.

ВЫРАЖЕНИЯ, СОДЕРЖАЩИЕ СТЕПЕНИ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ

Преобразование выражений, содержащих степени с целыми показателями. Стандартный вид числа.

ГЛАВА VII. ФУНКЦИИ И ГРАФИКИ (17ч)

ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ФУНКЦИЙ

Функция, область определения и область значений функции. Растяжение и сжатие графиков. Параллельный перенос графиков функций.

СВОЙСТВА И ГРАФИКИ НЕКОТОРЫХ ФУНКЦИЙ

Функции у=х^-1 и у = х^-2. Обратная пропорциональность и ее график. Дробно-линейная функция и ее график.

ИТОГОВОЕ ПОВТОРЕНИЕ (11ч)

Учебно-тематический план

Требования к уровню подготовки обучающихся.

В объем получаемых знаний входят те знания, умения и навыки, обязательное приобретение которых всеми учащимися предусмотрено требованиями программы общеобразовательной школы, однако преполагается иное, более высокое качество их сформированности.

Учащиеся должны приобрести умения решать задачи более высокой по сравнению с обязательным уровнем сложности:

В результате изучения алгебры ученик должен

знать/понимать

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• описывать свойства изученных функций, строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами;

Элементы логики, комбинаторики,
статистики и теории вероятностей

уметь

• проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

• решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;

• вычислять средние значения результатов измерений;

• находить частоту события, используя собственные наблюдения и готовые статистические данные;

• находить вероятности случайных событий в простейших случаях;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выстраивания аргументации при доказательстве (в форме монолога и диалога);

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов;

• сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;

• понимания статистических утверждений.

• Точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач;

• правильно пользоваться математической терминологией и символикой;

• применять рациональные приемы вычислений и тождественных преобразований;

• использовать наиболее употребительные эвристические приемы

В результате изучения курса алгебры 8-го класса учащиеся должны уметь:

• систематизировать сведения о рациональных и получить первоначальные представления об иррациональных числах;

• бегло и уверенно выполнять арифметические действия с рациональными числами; вычислять значения числовых выражений, содержащих степени и корни; научиться рационализировать вычисления;

• применять определение и свойства арифметических квадратных корней для вычисления значений числовых выражений и преобразования алгебраических выражений, содержащих квадратные корни;

• решать квадратные уравнения и уравнения, сводящиеся к ним, используя приемы и формулы для решения различных видов квадратных уравнений, графический способ решения уравнений; задачи, сводящиеся к решению квадратных уравнений;

• решать линейные неравенства с одной переменной, используя понятие числового промежутка и свойства числовых неравенств, системы линейных неравенств, задачи, сводящиеся к ним;

• понимать графическую интерпретацию решения уравнений и систем уравнений, неравенств;

• понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств; строить графики функций – линейной, прямой и обратной пропорциональностей, квадратичной функции и функции ;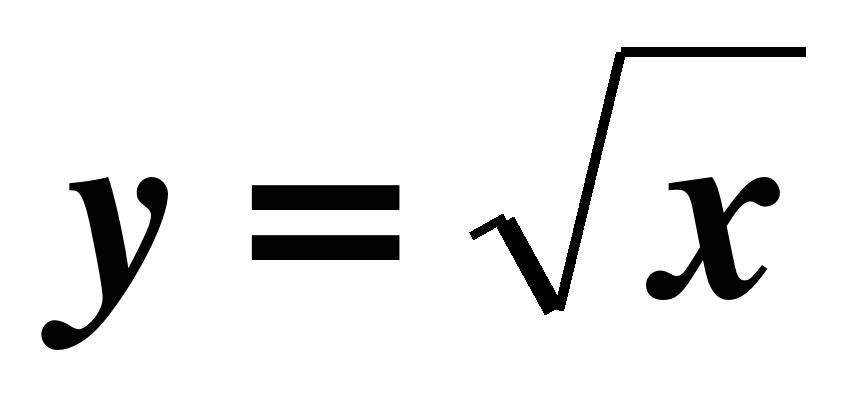

• использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:

  • решения практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;

  • устной прикидки, и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;

  • интерпретации результата решения задач.

Литература:

1. Артюнян Е. Б., Волович М. Б., Глазков Ю. А., Левитас Г. Г. Математические диктанты для 5-9 классов. – М.: Просвещение, 1991.

2. Жохов В. И., Макарычев Ю. Н., Миндюк Н. Г. Дидактические материалы по алгебре, 8 класс. – М.: Просвещение, 2008.

3. Звавис А. И., Шляпочкин Л. Я. Контрольные и проверочные по алгебре 7-9 классы. М.: Просвещение, 2003.

4. Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Феоктистов И.Е. Алгебра 8.(углубление) – М.: Мнемозина, 2008.

5. А.П. Ершова, В.В. Голобородько, А.С. Ершова. Алгебра 8. Самостоятельные и контрольные работы.- М.: Илекса, 2008.