. МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ - ГИМНАЗИЯ С.ЧЕКМАГУШ МУНИЦИПАЛЬНОГО РАЙОНА ЧЕКМАГУШЕВСКИЙ РАЙОН РЕСПУБЛИКИ БАШКОРТОСТАН
Рассмотрен Согласован Утвержден
на заседании кафедры зам.директора по УВР приказом № ___
Протокол № ____ ________ /Саматова З.В../ от «___» __________ 2014 г.
от «___» __________ 2014 г. от «___» __________ 2014 г. Директор ________ /Камильянов Р.Ф./
Рабочая программа
по алгебре
7 класс
Количество часов – 102
Учитель Арсланова Лилия Мадхатовна
Рабочая программа разработана на основе примерной программы по учебным предметам математика 5-9 классы - 3-е издание, переработанное – М. Просвещение. 2011 (Стандарты второго поколения).Предметная линия учебников А.Г.Мордковича 7-9классы.М.:Мнемозина,2012.
2014
Пояснительная записка.
Рабочая программа составлена для учащихся 7 «б,г» классов МБОУ Гимназия с.Чекмагуш, рассчитана на 102 часа в год,
3 часа в неделю.
Рабочая программа по алгебре разработана на основании Закона РФ «Об образовании» в соответствии с требованиями ФГОС общего образования и требования к оснащению образовательного процесса примерной программы по математике общего образования, авторской программы А.Г. Мордковича (2007), учебного плана и локальных актов МБОУ Гимназия с.Чекмагуш.
В основу изучения курса положены концепция:
дидактические (научности, сознательности и активности, наглядности, систематичности и последовательности, прочности, доступности, связи обучения с жизнью);
воспитания (социальной активности, социального творчества, развивающее воспитание, мотивированность, проблемность, индивидуализация, опора на ведущую деятельность);
развития (деятельности, непрерывности, целостного представления о мире, минимакса, психологической комфортности, вариативности, творчества);
педагогики здоровья: ненанесения вреда; субъект-субъектного взаимоотношения с учащимися; соответствия содержания и организации обучения возрастным особенностям учащихся; гармоничного сочетания обучающих, воспитывающих и развивающих педагогических воздействий; приоритет активных методов обучения; принцип отсроченного результата.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Это определило цели обучения :
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
На основании требований Государственного образовательного стандарта 2004 г. в содержании календарно-тематического планирования предполагается реализовать актуальные в настоящее время компетентностный, личностно ориентированный, деятельностный подходы, которые определяют задачи обучения:
приобретение математических знаний и умений;
овладение обобщенными способами мыслительной, творческой деятельностей;
• освоение компетенций: учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной и профессионально-трудового выбора.
С учетом возрастных особенностей классов выстроена система учебных занятий (уроков), спроектированы цели, задачи, ожидаемые результаты обучения (планируемые результаты), Требования к результатам обучения конкретизированы, даны в деятельностной формулировке ив последовательности их изложения. Конкретно сформулированные требования позволят спланировать виды учебной деятельности, что обеспечит усвоение учебного материала на уровне требований Государственного стандарта. В планировании приведены примерные измерители достижения требований к уровню подготовки. Планируется использование новых педагогических технологий в преподавании предмета.
В пояснительных записках программ указан достаточно полный перечень учебной и учебно-методической литературы для обучающихся и учителей.
Календарно-тематические планы рекомендуется рассматривать как ориентировочные. Они предполагают творческое их использование в отношении распределения учебного материала и времени на изучение различных тем, последовательности их рассмотрения, замены или привлечения дополнительного дидактического материала, выбора форм, методов, приемов обучения, видов самостоятельной деятельности в рамках требований Государственного стандарта математического образования. В ходе освоения содержания курса учащиеся получают возможность
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить логическое мышление и речь — умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контр примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Согласно федеральному базисному учебному плану на изучение алгебры в 7 классе отводится не менее 102 часов из расчета 3ч в неделю. В тематическом и поурочном планировании курсивом выделены темы, которые рассматриваются на уроке, но не выносятся на контроль.
Сроки реализации программы 1 год.
Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре
1. Оценка письменных контрольных работ, обучающихся по алгебре.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Отметка «1» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по алгебре.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Общая характеристика учебного предмета.
Рабочая программа составлена на основе:
-федерального компонента государственного стандарта общего образования,
-примерной программы по математике основного общего образования,
-федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2014-15 учебный год,
-с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования,
-авторского тематического планирования учебного материала, Примерной и авторской программы основного общего образования по математике Программы. Математика. 5-6 классы Алгебра. 7-9 классы. Алгебра и начала математического анализа 10-11 классы (авт.- сост. И.И.Зубарева, А.Г, Мордкович. – 2-е изд., испр. и доп. – М.: Мнемозина, 2009. – 63 с.).
-базисного учебного плана на 2014-15учебный год.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры. На основании авторской программы А.Г.Мордковича выделяется 5 часов на изучение курса «Элементы теории вероятностей и математической статистики». А.Г. Мордкович оставляет выбор за учителем, либо изучить весь курс (21 час) «Элементы теории вероятностей и математической статистики» в 9 классе, либо данный курс изучать по частям в 7 – 8 – 9 классах. Изучение данного курса предполагается изучать по частям в 7 – 8 – 9 классах с таким расчетом, что к итоговой аттестации учеников за курс средней школы данный курс будет пройден полностью. Изучение данного курса ориентировано на использование пособия авторов Мордкович А.Г., Семёнов П.В. «События. Вероятности. Статистическая обработка данных». Пособие предназначено для ознакомления учащихся с элементами теории вероятностей и математической статистики и состоит из дополнительных параграфов к курсу алгебры 7 – 9 классов общеобразовательных учреждений.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану на изучение математики в 7 классе отводится не менее 102 часов из расчета 3ч в неделю. В тематическом и поурочном планировании курсивом выделены темы, которые рассматриваются на уроке, но не выносятся на контроль.
Описание ценностных ориентиров содержания учебного предмета
Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения алгебры к изучению действительности и решению практических задач. Главная задача УМК А.Г. Мордковича заключается не в сухом сообщении математических фактов, а в развитии учащихся посредством продвижения в предмете, т.е. приоритетным является не информационное, а развивающее поле курса.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений). Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Личностные, метапредметные и предметные результаты освоения учебного предмета
Личностные результаты отображают готовность и способность обучающихся к саморазвитию, ценностно-смысловые установки и личностные качества; сформированность основ российской, гражданской идентичности:
1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
2) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
4) креативность мышления, инициатива, находчивость, активность при решении математических задач;
5) умение контролировать процесс и результат учебной математической деятельности;
6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ
В результате изучения курса алгебры, обучающиеся должны знать:
математический язык;
свойства степени с натуральным показателем;
определение одночлена и многочлена, операции над одночленами и многочленами; формулы сокращенного умножения; способы разложения на множители;
линейную функцию, её свойства и график;
квадратичную функцию и её график;
способы решения системы двух линейных уравнений с двумя переменными;
должны уметь:
составлять математическую модель при решении задач;
выполнять действия над степенями с натуральными показателями, показателем, не равным нулю, используя свойства степеней;
выполнять арифметические операции над одночленами и многочленами, раскладывать многочлены на множители, используя метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения;
строить графики линейной и квадратичной функций;
решать системы двух линейных уравнений с двумя переменными;
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения.
Решать следующие жизненно-практические задачи:
самостоятельно приобретать и применять знания в различных ситуациях;
работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других;
извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем, энциклопедией и справочником для нахождения информации;
самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем;
выстраивания аргументации при доказательстве;
распознавания логически некорректных рассуждений.
Метапредметные результаты освоения основной образовательной программы по алгебре основного общего образования должны отражать:
1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
6) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
7) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
8) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
9)умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера
Предметные результаты представляют собой освоенный обучающимися опыт деятельности по получению нового знания, его преобразованию и применению, а также систему основополагающих элементов научного знания:
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Формы контроля
- Устный счёт
- Устный опрос
- Фронтальный опрос
- Самостоятельная работа
- Индивидуальное задание
- Математический тест
-Математический диктант
- Практическая работа
-Контрольная работа
Типы уроков
-Урок ознакомления с новым материалом
-Урок закрепления изученного
-Урок применения знаний и умений
-Урок обобщения и систематизации знаний
-Урок проверки и коррекции знаний и умений
-Комбинированный урок
-Урок коррекции знаний
Основное содержание.
Математический язык. Математическая модель.(9ч.)
Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математическая модель реальных ситуаций. Координатная прямая, виды промежутков на ней.
Линейная функция.(15ч.)
Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки M (a; b) в прямоугольной системе координат.
Линейное уравнение с двумя переменными. Решение уравнения ax + by + c = 0. График уравнения. Алгоритм построения графика уравнения ax + by + c = 0.
Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции.
Линейная функция y = kx и её график.
Взаимное расположение графиков линейных функций.
Системы двух линейных уравнений с двумя переменными.(14ч.)
Система уравнений. Решение системы уравнений. Графический метод решения системы уравнений. Метод подстановки. Метод алгебраического сложения.
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи).
Степень с натуральным показателем.(9ч.)
Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.
Одночлены. Операции над одночленами.(10ч.)
Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены.
Сложение одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.
Многочлены. Арифметические операции над многочленами.(19ч.)
Многочлен. Члены многочлена. Двучлен. Трёхчлен. Произведение подобных членов. Стандартный вид многочлена.
Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен.
Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов.
Деление многочлена на одночлен.
Разложение многочленов на множители.(21ч.)
Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения, комбинации различных приёмов. Метод выделения полного квадрата.
Понятие алгебраической дроби. Сокращение алгебраической дроби.
Тождество. Тождественно равные выражения. Тождественные образования.
Функция y=x2 .(8ч.)
Функция y=x2 , её свойства и график. Графическое решение уравнений. Что означает в математике запись y=f(x).
Календарно-тематическое планирование.
| Номер урока | Содержание учебного материала, количество часов | Основные виды деятельности учащихся (на уровне учебных действий) | Дата проведения урока по плану | Дата проведения урока фактически |
| Математический язык. Математическая модель.9ч
|
|
| 1-4
5-6
7-8
| Числовые и алгебраические выражения. 4ч. Что такое математический язык. 2ч. Что такое математическая модель.2ч.
| Выполнять элементарные знаково-символические действия, применять буквы для обозначения чисел, для записи общих утверждений; составлять буквенные выражения по условиям, заданным словесно, рисунком или чертежом; преобразовывать алгебраические суммы и произведения (выполнять приведение подобных слагаемых, раскрытие скобок, упрощение произведений). Вычислять числовое значение буквенного выражения; находить область допустимых значений переменных в выражении. Распознавать линейные уравнения, решать линейные уравнения, а также уравнения, сводящиеся к ним. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления уравнения; решать составленное уравнение; интерпретировать результат.
|
|
|
| 9 | Контрольная работа №1.1ч. | применять изученный теоретический материал при выполнении письменной работы |
|
|
|
|
|
|
|
|
|
10-11
12-13
14-16
17-19
20-21
22-23 | Линейная функция.15ч |
|
| Координатная прямая.2ч.
Координатная плоскость.2ч.
Линейное уравнение с двумя переменными и его график.3ч.
Линейная функция и ее график.3ч
Линейная функция y=kx.2ч.
Взаимное расположение графиков линейных функций.2ч. | Строить на координатной плоскости точки и фигуры по заданным координатам; определять координаты точек. Определять, является ли пара чисел решением данного уравнения с двумя переменными; приводить примеры решений уравнений с двумя переменными; решать задачи, алгебраической моделью которых является уравнение с двумя переменными; находить целые решения путем перебора. Строить графики линейных уравнений с двумя переменными. Вычислять значения линейных функций, составлять таблицы значений функции. Строить график линейной функции, описывать ее свойства на основе графических представлений. Показывать схематически положение на координатной плоскости графиков функций y=kx, y=kx+b, в зависимости от значений коэффициентов. |
|
|
| 24. | Контрольная работа№2 «Линейная функция» | применять изученный теоретический материал при выполнении письменной работы |
|
|
| Система двух линейных уравнений с двумя переменными.14ч
|
| 25-26
27-30
31-33
34-37 | Основные понятия.2ч.
Метод подстановки.4ч.
Метод алгебраического сложения.3ч.
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.4ч. | Решать системы двух линейных уравнений с двумя переменными графически, методом подстановки, методом алгебраического сложения. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления системы уравнений; решать составленную систему уравнений; интерпретировать результат. Исследовать системы уравнений с двумя переменными, содержащие буквенные коэффициенты. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Использовать функционально-графические представления для решения и исследования систем уравнений. |
|
|
| 38
| Контрольная работа№3 «Система линейных уравнений» | применять изученный теоретический материал при выполнении письменной работы |
|
|
|
Степень с натуральным показателем и ее свойства.9ч
|
|
| 39
40
41-43
44-45
46
47
| Что такое степень с натуральным показателем.1ч.
Таблица основных степеней.1ч.
Свойства степеней с натуральными показателями.3ч
Умножение и деление степеней с одинаковыми показателями.2ч
Степень с нулевым показателем.1ч.
Контрольная работа №4 | Формулировать определение степени с натуральным показателем, с нулевым показателем; формулировать, записывать в символической форме и обосновывать свойства степени с целым неотрицательным показателем; применять свойства степени для преобразования выражений и вычислений. Воспроизводить формулировки определений, конструировать несложные определения самостоятельно. Воспроизводить формулировки и доказательства изученных теорем. Конструировать математические предложения с помощью связок если…, то…,
применять изученный теоретический материал при выполнении письменной работы |
|
|
|
Одночлены. Арифметические операции над одночленами.10ч.
|
|
| 48-49
50-52
53-54
55-56
| Понятие одночлена. Стандартный вид одночлена.2ч
Сложение и вычитание одночленов.3ч
Умножение одночленов. Возведение одночленов в натуральную степень.2ч
Деление одночлена на одночлен.2ч | Выполнять действия с одночленами. |
|
|
| 57
| Контрольная работа «Свойства степеней» | применять изученный теоретический материал при выполнении письменной работы |
|
|
| Многочлены. Арифметические операции над одночленами.19ч
|
| 58-59
60-61
62-64
65-66
| Основные понятия.2ч
Сложение и вычитание многочленов.2ч
Умножение многочлена на одночлен.3ч
Умножение многочлена на многочлен.2ч | Выполнять действия с многочленами. Выводить формулы сокращенного умножения, применять их в преобразованиях выражений и вычислениях. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
| 67
| Контрольная работа № 6
| применять изученный теоретический материал при выполнении письменной работы |
|
|
| 68-69
70-71
72-73
74-75 | Формулы сокращенного умножения. Квадрат суммы и квадрат разности.2ч
Формулы сокращенного умножения. Разность квадратов.2ч.
Формулы сокращенного умножения. Разность кубов и сумма кубов.2ч.
Деление многочлена на одночлен.2ч
|
|
|
|
| 76 | Контрольная работа№7 «Многочлены».1ч | применять изученный теоретический материал при выполнении письменной работы |
|
| Разложение многочленов на множители.21ч. |
| 77
78-80 81-83
84-88
89-92 93
| Что такое разложение многочленов на множители.1ч.
Вынесение общего множителя за скобки.3ч.
Способ группировки.3ч.
Разложение многочлена на множители с помощью формул сокращенного умножения.5ч
Разложение многочленов на множители с помощью комбинации различных приемов.4ч. Контрольная работа №8 |
применять изученный теоретический материал при выполнении письменной работы
|
|
|
| 94-96
97 | Сокращение алгебраических дробей.3ч
Тождества.1ч | Выполнять разложение многочлена на множители и сокращение алгебраических дробей. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
| Функция y=x².8ч
|
| 98-101
102
| Функция y=x².1ч
Графическое решение уравнений.1ч
Что означает запись y=f(x).2ч
Контрольная работа № 9. | Вычислять значения функций y=x² и y= –x², составлять таблицы значений функции. Строить графики функции y=x² и y= –x² и кусочных функций, описывать их свойства на основе графических представлений. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии.
Способность к организации самостоятельной и коллективной деятельности в ходе решения учебных и исследовательских проблем (поиск, обработка, презентация информации); самостоятельно приобретать с помощью информационных технологий и использовать в практической деятельности новые знания и умения; Анализировать и оценивать результаты исследований; излагать мысли в устной и письменной форме; Представлять результаты исследовательской деятельности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Описание материально-технического обеспечения образовательного процесса.
Основная литература для учителя:
Мордкович А.Г. «Алгебра-7» часть 1, учебник – М.: Мнемозина, 2012
Мордкович А.Г., Александрова Л.А., Мишустина Т.Н., Тульчинская Е.Е. «Алгебра.7класс» часть 2, задачник – М.: Мнемозина, 2012
Александрова Л.А. «Контрольные работы. Алгебра -7» - М.: Мнемозина, 2009
Александрова Л.А. «Самостоятельные работы. Алгебра -7» - М.: Мнемозина, 2009
Дополнительная литература:
1. «Нестандартные задания по математике 5 – 11 классы», В.В. Кривоногов.
2. «Математика, итоговые уроки 5-9 классы», О.В. Бощенко.
3. «Математические олимпиады в школе 5-11 классы», А.В. Фарков.
4. «Тесты для промежуточной аттестации 7-8 классы», Ф.Ф. Лысенко, 2007 г.
5. «Математические диктанты для 5-9 классов» / Е. Б. Арутюнян. - М., 1995.
Интернет ресурсы:
http://uchitmatematika. ucos. ru/
http:// mikhatoval. edum. ru/
http://yroki. net
http:// rusedi.ru/
Основная литературы для ученика
1.Мордкович А.Г. «Алгебра-7» часть 1, учебник – М.: Мнемозина, 2012
2.Мордкович А.Г., Александрова Л.А., Мишустина Т.Н., Тульчинская Е.Е. «Алгебра.7класс» часть 2, задачник – М.: Мнемозина, 2012
Дополнительная литература для ученика: Звавич «Дидактические материалы по алгебре, 7 класс»
Список литературы:
Арутюнян, Е. Б. Математические диктанты для 5-9 классов / Е. Б. Арутюнян. - М., 1995.
Заболотнева Н.В. Олимпиадные задания по математике. 5-8 классы: 500 нестандартных задач для проведения конкурсов и олимпиад: развитие творческой сущности учащихся. Волгоград: Учитель, 2006.
Лысенко, Ф. Ф. Учебно-тренировочные тестовые задания «малого» ЕГЭ по математике / Ф. Ф. Лысенко. - Ростов н/Д: Легион, 2008.
Пичурин, Л. Ф. За страницами учебника алгебры /. - М., 1990.
Студенецкая В.Н. Математика. Система подготовки учащихся к ЕГЭ: пособие для учителя /. - Волгоград: Учитель, 2004.
Математика: еженедельное приложение к газете «Первое сентября».
Математика в школе: ежемесячный научно-методический журнал.
Мультимедийный компьютер; проектор; экран; интернет. Интерактивная доска PROMETHEAN
10.Контрольно- измерительные материалы
Перечень обязательных контрольных работ:
Контрольная работа №1: «Выражения, преобразования выражений, тождества»
Контрольная работа №2: «Линейные уравнения с одной переменной».
Контрольная работа №3: «Линейная функция»
Контрольная работа №4: «Степень с натуральным показателем».
Контрольная работа №5: «Многочлен».
Контрольная работа №6: «Умножение многочленов. Способ группировки».
Контрольная работа №7: «Разложение многочлена на множители».
Контрольная работа №8: «Системы линейных уравнений с двумя переменными».
Итоговая контрольная работа.
Темы творческих проектов:
-Модуль числа.
-Математика и законы красоты.







МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ - ГИМНАЗИЯ С.ЧЕКМАГУШ МУНИЦИПАЛЬНОГО РАЙОНА ЧЕКМАГУШЕВСКИЙ РАЙОН РЕСПУБЛИКИ БАШКОРТОСТАН
Рассмотрен Согласован Утвержден
на заседании кафедры зам.директора по УВР приказом № ___
Протокол № ____ ________ /Саматова З.В../ от «___» __________ 2014 г.
от «___» __________ 2014 г. от «___» __________ 2014 г. Директор ________ /Камильянов Р.Ф./
Рабочая программа
по геометрии
7 класс
Количество часов –68
Учитель Арсланова Лилия Мадхатовна
Рабочая программа разработана на основе примерной программы по учебным предметам математика 5-9 классы - 3-е издание, переработанное – М. Просвещение. 2011 (Стандарты второго поколения).Предметная линия учебников Л.С.Атанасян, В.Ф.Бутузова,С.Б.Кадомцева и др.-М.Просвещение,2009
2014
Пояснительная записка
Рабочая программа составлена для учащихся 7 «б,г» классов МБОУ Гимназия с.Чекмагуш, рассчитана на 68 часов в год,
2 часа в неделю.
Овладение учащимися системой геометрических знаний и умений необходимо в повседневной жизни для изучения смежных дисциплин и продолжения образования.
Практическая значимость школьного курса геометрии обусловлена тем, что её объектом являются пространственные формы и количественные отношения действительного мира. Геометрическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, геометрия развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.
Цели изучения курса геометрии:
развивать пространственное мышление и математическую культуру;
учить ясно и точно излагать свои мысли;
формировать качества личности необходимые человеку в повседневной жизни: умение преодолевать трудности, доводить начатое дело до конца;
помочь приобрести опыт исследовательской работы.
Важнейшей задачей школьного курса геометрии является развитие логического мышления учащихся. Сами объекты геометрических умозаключений и принятые в геометрии правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить четкие определения, развивают логическую интуицию, кратко и наглядно вскрывают механизм логических построений и учат их применению. Тем самым геометрия занимает ведущее место в формировании научно-теоретического мышления школьников.
Задачи обучения:
-ввести основные геометрические понятия, научить различать их взаимное расположение;
-научить распознавать геометрические фигуры и изображать их;
-ввести понятия: теорема, доказательство, признак, свойство;
-изучить все о треугольниках (элементы, признаки равенства);
-изучить признаки параллельности прямых и научить применять их при решении задач и доказательстве теорем;
-научить решать геометрические задачи на доказательства и вычисления;
-подготовить к дальнейшему изучению геометрии в последующих классах.
Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, способствуя восприятию геометрических форм, усвоению понятия симметрии, геометрия вносит значительный вклад в эстетическое воспитание учащихся. Её изучение развивает воображение школьников, существенно обогащает и развивает их пространственные представления. Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
научиться применять формально-оперативные алгебраические умения к решению геометрических задач;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами и их свойствами;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Общая характеристика курса геометрии в 7 классе
-федерального компонента государственного стандарта общего образования,
-примерной программы по математике основного общего образования,
-федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2013-14 учебный год,
-с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования,
-авторского тематического планирования учебного материала, Примерной и авторской программы основного общего образования по математике Программы. Математика. 5-6 классы Алгебра. 7-9 классы. Алгебра и начала математического анализа 10-11 классы ( авт.- сост. И.И.Зубарева, А.Г, Мордкович. – 2-е изд., испр. и доп.. – М.: Мнемозина, 2009. – 63 с.).
-базисного учебного плана на 2013-14учебный год.
Математическое образование в основной школе складывается из следующих содержательных компонентов (блоков): «Арифметика», «Алгебра», «Геометрия», «Элементы логики, комбинаторики, статистики и теории вероятностей».
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Основная форма организации образовательного процесса—классно-урочная система. Предусматривается применение следующих технологий обучения:
-традиционная классно-урочная;
-игровые технологии;
-технологии уровневой дифференциации;
-элементы проблемного обучения;
-здоровьесберегающие технологии;
-ИКТ.
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному (образовательному) плану для образовательных учреждений Российской Федерации на изучение геометрии в 7 классе отводится не менее 50 годовых часов из расчета 2 часов в неделю. Рабочая программа рассчитана на 68 учебных часов (2 часа в неделю).
Описание ценностных ориентиров содержания учебного предмета
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В курсе геометрии 7 класса систематизируются знания обучающихся о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вводится понятие теоремы; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится новый класс задач - на построение с помощью циркуля и линейки; вводится одно из важнейших понятий - понятие параллельных прямых; даётся первое представление об аксиомах и аксиоматическом методе в геометрии; вводится аксиома параллельных прямых; рассматриваются новые интересные и важные свойства треугольников в данной теме доказывается одна из важнейших теорем геометрии — теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников. Приоритетом общего образования является формирование общеучебных умений и навыков, уровень освоения которых в значительной мере предопределяет успешность всего последующего обучения. Развитие личностных качеств и способностей школьников опирается на приобретение ими опыта разнообразной деятельности: учебно-познавательной, практической, социальной. Для подтверждения успешности обучения ученика на уроках будут использованы следующие виды работ: работа в группах, работа в парах, индивидуальная и дифференцированная работа, составление таблиц, схем, подготовка сообщений, докладов, рефератов, сравнение, анализ, работа с различными источниками информации.
В 7 классе закладываются основы геометрических умений – в доказательствах, рассуждениях, обоснованиях и построениях, рассматриваются главные определения, важные методы доказательств и решений задач.
Личностные, метапредметные и предметные результаты освоения содержания курса
Программа обеспечивает достижение следующих результатов:
личностные:
формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов;
формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении геометрических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовых связей;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способу работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
овладение навыками устных, письменных, инструментальных вычислений;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне – о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров геометрических фигур (треугольника);
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использование при необходимости справочных материалов, калькулятора, компьютера.
Материалы для рабочей программы составлены на основе:
-федерального компонента государственного стандарта общего образования,
-примерной программы по математике основного общего образования,
-федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2014-15 учебный год, с учетом требований к оснащению образовательного процесса в соответствии с содержанием учебных предметов компонента государственного стандарта общего образования, авторского тематического планирования учебного материала,
-базисного учебного плана 2014-2015 года.
Основное содержание курса
1. Начальные геометрические сведения (10 ч) Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые. Основная цель — систематизировать знания учащихся о простейших геометрических фигурах и их свойствах; ввести понятие равенства фигур. В данной теме вводятся основные геометрические понятия и свойства простейших геометрических фигур на основе наглядных представлений учащихся путем обобщения очевидных или известных из курса математики 1—6 классов геометрических фактов. Понятие аксиомы на начальном этапе обучения не вводится, и сами аксиомы не формулируются в явном виде. Необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приводятся в описательной форме. Принципиальным моментом данной темы является введение понятия равенства геометрических фигур на основе наглядного понятия наложения. Определенное внимание должно уделяться практическим приложениям геометрических понятий.
Учащиеся должны уметь:
- формулировать определения и иллюстрировать понятия отрезка, луча; угла, прямого, острого, тупого и развернутого углов; вертикальных и смежных углов; биссектрисы угла;
- формулировать и доказывать теоремы, выражающие свойства вертикальных и смежных углов;
- формулировать определения перпендикуляра к прямой;
- решать задачи на доказательство и вычисления, применяя изученные определения и теоремы;
- опираясь на условие задачи, проводить необходимые доказательные рассуждения;
- сопоставлять полученный результат с условием задачи.
Перечень контрольных мероприятий:
Контрольная работа №1 «Начальные геометрические сведения»
2.Треугольники (18 ч) Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.
Основная цель — ввести понятие теоремы; выработать умение доказывать равенство треугольников с помощью изученных признаков; ввести новый класс задач — на построение с помощью циркуля и линейки. Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательство большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников — обоснование их равенства с помощью какого-то признака — следствия, вытекающие из равенства треугольников. Применение признаков равенства треугольников при решении задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами.
Учащиеся должны уметь:
- распознавать на чертежах, формулировать определения, изображать равнобедренный, равносторонний треугольники; высоту, медиану, биссектрису;
- формулировать определение равных треугольников;
- формулировать и доказывать теоремы о признаках равенства треугольников;
- объяснять и иллюстрировать неравенство треугольника;
- формулировать и доказывать теоремы о свойствах и признаках равнобедренного треугольника,
- моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения;
- решать задачи на доказательство и вычисления, применяя изученные определения и теоремы;
- опираясь на условие задачи, проводить необходимые доказательные рассуждения;
- интерпретировать полученный результат и сопоставлять его с условием задачи;
- решать основные задачи на построение с помощью циркуля и линейки: деление отрезка пополам; построение угла, равного данному; построение треугольника по трем сторонам; построение перпендикуляра к прямой; построение биссектрисы угла; деление отрезка на и равных частей.
Контрольная работа №2 «Треугольники»
3. Параллельные прямые (13 ч) Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Основная цель — ввести одно из важнейших понятий — понятие параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых. Признаки и свойства параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными), широко используются в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии.
Учащиеся должны уметь:
- распознавать на чертежах, изображать, формулировать определения параллельных прямых; углов, образованных при пересечении двух параллельных прямых секущей; перпендикулярных прямых; перпендикуляра и наклонной к прямой; серединного перпендикуляра к отрезку;
- формулировать аксиому параллельных прямых;
- формулировать и доказывать теоремы, выражающие свойства и признаки параллельных прямых;
- моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения;
- решать задачи на доказательство и вычисления, применяя изученные определения и теоремы;
- опираясь на условие задачи, проводить необходимые доказательные рассуждения;
- интерпретировать полученный результат и сопоставлять его с условием задачи.
Контрольная работа №3 «Параллельные прямые»
4. Соотношения между сторонами и углами треугольника (18 ч) Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам. Основная цель — рассмотреть новые интересные и важные свойства треугольников. В данной теме доказывается одна из важнейших теорем геометрии — теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников. Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теоремы о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, в частности используется в задачах на построение. При решении задач на построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи.
Учащиеся должны уметь:
- распознавать на чертежах, формулировать определения, изображать прямоугольный, остроугольный, тупоугольный;
- формулировать и доказывать теоремы
— о соотношениях между сторонами и углами треугольника,
- о сумме углов треугольника,
- о внешнем угле треугольника;
- формулировать свойства и признаки равенства прямоугольных треугольников;
- решать задачи на построение треугольника по трем его элементам с помощью циркуля и линейки.
Контрольная работа №4 «Соотношения между сторонами и углами треугольника»
Контрольная работа №5 «Прямоугольные треугольники. Построение треугольника по трем элементам»
5. Повторение (10 ч)
Итоговая контрольная работа
Требования к уровню подготовки обучающихся 7 класса по геометрии.
Планируемый уровень подготовки выпускников на конец ступени в соответствии с требованиями, установленным федеральными государственными образовательными стандартами:
В результате изучения математики ученик должен знать/понимать
существо понятия математического доказательства; приводить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
***Помимо указанных в данном разделе знаний, в требования к уровню подготовки включаются и знания, необходимые для применения перечисленных ниже умений.
В результате изучения геометрии ученик должен уметь:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур; распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их; в простейших случаях строить сечения и развертки пространственных тел; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами; вычислять значения геометрических величин (длин, углов, площадей, объемов); в том числе: для углов от 0° до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них; решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии; проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования; решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии; расчетов, включающих простейшие тригонометрические формулы; решения геометрических задач с использованием тригонометрии; решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства); построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Организационно – педагогические условия реализации данной рабочей программы.
I. Требования к тетрадям обучающихся по геометрии:
В тетрадях должны быть грамотно оформлены все записи, писать разборчивым почерком. Поля в обязательном порядке выделяются в рабочих тетрадях, для контрольных работ по всем предметам. Дата записывается на полях цифрами (9.09. 09). Обязательно соблюдение красной строки. Подчеркивания и чертежи выполнять аккуратно. Таблицы, условные обозначения, чертежи выполнять карандашом, в случае необходимости с применением линейки. Исправление ошибок: зачеркивать косой линией (ручкой), часть слова, слово, предложение – тонкой горизонтальной линией, вместо зачеркнутого надписать нужную запись. В 7 классе – проверка тетрадей производится красной пастой. В тетрадях для контрольных работ не применять штрих. Не должно быть посторонних записей, рисунков в рабочих тетрадях.Количество ученических тетрадей.По геометрии должно быть по две рабочей тетради и тетради для контрольных работ. Допускаются тетради на печатной основе.Порядок проверки письменных работ учителями.Рабочие тетради обучающихся 7 класса по геометрии проверяются выборочно, но не реже 1 раза неделю. Контрольные, рабочие тетради на печатной основе проверяются и возвращаются к следующему уроку.
II. Требования к опросу на уроке.
Частотность опроса должна быть не менее одного раза в 3-4 урока. Комбинированный опрос должен быть отражен записью в журнале (практические, тесты, диктанты и другие виды работ). При монологическом опросе обучающийся дает ответ стоя, при фронтальном опросе, дискуссии он может не вставать с места. По окончании урока оценки за опрос обучающимся выставляются в дневник и в журнал. Тесты должны быть распечатаны или представлены в электронном виде. Не должно быть тестов «на слух», оценок только за письменные работы.
Домашнее задание. Объем домашнего задания не должен превышать норм Санпина. Домашнее задание записывается в дневник. Письменные работы проверяются в соответствии с орфографическим режимом (ошибки в терминах, названиях учитывать). Проверка д/з должна осуществляться в разных формах. Д/з записывается в журнале в соответствии с календарно – тематическим планом. Отставание по программе не ликвидировать за счёт д/з.
12.Критерии и нормы оценки знаний, умений и навыков обучающихся по геометрии. 1. Оценка письменных контрольных работ обучающихся по геометрии.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны;
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах.
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по геометрии.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Сроки реализации программы 1 год.
3.Общая характеристика учебного предмета.
Рабочая программа составлена на основе:
-федерального компонента государственного стандарта общего образования,
-примерной программы по математике основного общего образования,
-федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2014-15 учебный год,
-с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования,
-авторского тематического планирования учебного материала, Примерной и авторской программы основного общего образования по математике Программы -базисного учебного плана на 2014-15учебный год.
Требования к уровню подготовки учащихся к предмету «Геометрия»
В результате изучения математики ученик должен
знать/понимать:
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь:
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
находить стороны, углы и периметры треугольников, длины ломаных;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие формулы;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Описание материально-технического обеспечения образовательного процесса:
Библиотечный фонд. Нормативные документы:
1.1. Федеральный государственный стандарт общего среднего образования.
1.2. Примерные программы по учебным предметам. Математика. 5-9 классы.
1.3. Сборник нормативных документов. Математика / сост. Э.Д.Днепров, А.Г.Аркадьев. – М.: Дрофа, 2009. – 128 с.
1.4. Программы для общеобразовательных учреждений: Геометрия 7 - 9 кл. / сост. Бурмистрова Т.А. - М.:
Просвещение, 2009.
1.5. Бутузов В.Ф. Геометрия. Рабочая программа к учебнику Л.С.Атанасяна и других. 7-9 классы: пособие для учителей общеобразов. учреждений / В.Ф.Бутузов. – М.: Просвещение, 2011. – 31 с.
2. Библиотечный фонд. Учебная литература основная:
2.1. Геометрия: 7 – 9. Учебник для общеобразовательных учреждений. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г.Позняк, И.И. Юдина. / М.: Просвещение, 2009 – 384 с.: ил.
3. Библиотечный фонд. Дополнительная литература для учителя:
3.1. Зив Б.Г. Геометрия. Дидактические материалы. 7 кл. / Б.Г.Зив, В.М.Мейлер. – 16-е изд. - М.: Просвещение, 2010. -127 с.: ил.
3.2. Изучение геометрии в 7, 8, 9 классах: метод. рекомендации: кн. для учителя / Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков и др. - М.: Просвещение, 2011.
3.3. Мищенко Т.М. Геометрия. Тематические тесты. 7 класс / Т.М.Мищенко, А.Д.Блинков. – 3-е изд., дораб. – М.: Просвещение, 2011. – 80 с.
3.4. Математические кружки в школе. 5-8 классы / А.В.Фарков. – 5-е изд. – М.: Айрис-пресс, 2008. – 144 с. – (Школьные олимпиады).
3.5. Математика. 5-11 классы: проблемно-развивающие задания, конспекты уроков, проекты / авт.-сост. Г.Б.Полтавская. –Волгоград: Учитель,2010. – 143 с.
3.6. Математика. 5-8 классы: игровые технологии на уроках. - 2-е изд., стереотип. / авт.-сост. И.Б.Ремчукова. – Волгоград: Учитель, 2008. – 99 с.
3.7. Обучение решению задач как средство развития учащихся: Из опыта работы: Методическое пособие для учителя. - Киров: Изд-во ИУУ, 1999 – 100 с.
4. Библиотечный фонд. Дополнительная литература для учащихся:
4.1. Энциклопедия. Я познаю мир. Великие ученые. – М.: ООО «Издательство АСТ», 2003.
4.2. Энциклопедия. Я познаю мир. Математика. – М.: ООО «Издательство АСТ», 2003.
4.3. Черкасов О.Ю. Математика. Справочник / О.Ю.Черкасов, А.Г.Якушев. -М.: АСТ-ПРЕСС ШКОЛА, 2006.
4.4. Мантуленко В.Г. Кроссворды для школьников. Математика / В.Г.Мантуленко, О.Г.Гетманенко. – Ярославль: Академия развития, 1998.
4.5. Энциклопедия для детей. Т.11. Математика / гл.ред. М.Д.Аксенова. – М.: Аванта+, 2002. – 688 с.
5. Дидактические материалы, рабочие тетради:
5.1. Геометрия: рабочая тетрадь: 7 кл. /Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков, И.И.Юдина. – М.: Просвещение, 2011.
Пособия и оборудование:
6.1. Справочники.
6.2. Математические таблицы Брадиса.
6.3. Печатные пособия (наглядные средства – таблицы).
6.4. Учебно-практическое и учебно-лабораторное оборудование:
а) раздаточный материал для практических и лабораторных работ,
б) модели геометрических плоских и пространственных фигур.
6.5. Медиаресурсы.
6.6. Технические средства обучения:
а) компьютер;
б) медиапроектор;
в) магнитная доска;
г) доска с координатной плоскостью.
7. Информационные средства (Интернет-ресурсы):
7.1. http://ilib.mirrorl.mccme.ru/
7.2. http://window.edu.ru/window/library/
7.3. http://www.problems.ru/
7.4. http://kvant.mirrorl.mccme.ru/
7.5. http://www.etudes.ru/
Список литературы: 1.Гаврилова Н.Ф. «Поурочные разработки по геометрии. 7класс». М.: «ВАКО»,2010,288с.- (В помощь школьному учителю)
Календарно-тематическое планирование
Учебный год: 2014/2015
Предмет: Геометрия, 7 класс
Учитель: Арсланова Л.М.
Количество часов за год: 68
Количество часов в неделю: 2
Количество контрольных работ: а) за первое полугодие - 2;
б) за год –5;
Количество лабораторных и других видов практических работ - нет
Базовый учебник: Геометрия 7-9 класс: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 17-е изд. - М.: Просвещение, 2009.
Используемая учебно-методическая литература: Н.Ф.Гаврилова. Поурочные разработки по геометрии 7 класс: кн. для учителя. – М.: «ВАКО», 2010. Тексты контрольных работ взяты из методической литературы: Программы общеобразовательных учреждений. Геометрия7-9 классы. Составитель Бурмистрова Т. А. – М.: Просвещение, 2009.
| № п/п | Тема раздела, урока | Кол-во часов | Основные термины, понятия | ЗУН | Оборудование для демонстраций, лабораторных, практических работ | Дата планируемая | Примечания |
|
| ГЛАВА I. НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ | 11 |
|
|
|
|
|
|
| §1. ПРЯМАЯ И ОТРЕЗОК. |
|
|
|
|
|
|
| 1
| Точки, прямые, отрезки. Провешивание прямой на местности, п.1, 2.
| 1
| Отрезок, прямая. | Знать, сколько прямых можно провести через две точки, сколько общих точек могут иметь две прямые, какая фигура называется отрезком; уметь обозначать точки и прямые на рисунке, изображать возможные случаи взаимного расположения точек и прямых, двух прямых, объяснить, что такое отрезок, изображать и обозначать отрезки на рисунке. | Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §2. ЛУЧ И УГОЛ. |
|
|
|
|
|
|
| 2
| Луч. Угол, п.3, 4. | 1
| Луч, угол. | Знать, какая геометрическая фигура называется углом, что такое стороны и вершина угла. Уметь обозначать неразвернутые и развернутые углы, показать на рисунке внутреннюю область угла, проводить луч, разделяющий угол на два угла. | Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §3. СРАВНЕНИЕ ОТРЕЗКОВ И УГЛОВ. |
|
|
|
|
|
|
| 3 | Равенство геометрических фигур. Сравнение отрезков и углов, п.5,6. | 1 | Равные фигуры, равные отрезки, равные углы. | Знать, какие геометрические фигуры называются равными, какая точка называется серединой отрезка, какой луч называется биссектрисой угла. Уметь сравнивать отрезки и углы и записывать результат сравнения, отмечать с помощью масштабной линейки середину отрезка, с помощью транспортира проводить биссектрису угла. | Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §4. ИЗМЕРЕНИЕ ОТРЕЗКОВ. |
|
|
|
|
|
|
| 4 | Длина отрезка, п.7.
| 1 | Длина отрезка. | Знать, что при выбранной единице измерения длина любого данного отрезка выражается положительным числом; уметь измерять данный отрезок с помощью линейки и выразить | Слайд-презентация, иллюстрация на доске.
|
|
|
| 5 | Единицы измерения. Измерительные инструменты, п.8. | 1 | Единица измерения. | его длину в сантиметрах, миллиметрах, метрах, находить длину отрезка в тех случаях, когда точка делит данный отрезок на два отрезка, длины которых известны, решать задачи типа 30 – 33, 35, 37. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 6 | §5. ИЗМЕРЕНИЕ УГЛОВ. |
|
|
|
|
|
|
| Градусная мера угла. Измерение углов на местности, п.9, 10. | 1 | Градусная мера угла, градус, транспортир. | Знать, что такое градусная мера угла, чему равны минута и секунда; уметь находить градусные меры данных углов, используя транспортир, Изображать прямой, острый, тупой, развернутый углы, решать задачи типа 47 – 50. | Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §6. ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ. |
|
|
|
|
|
|
| 7 | Смежные и вертикальные углы, п.11. | 1 | Смежные, вертикальные углы. | Знать, какие углы называются смежными и чему равна сумма смежных углов, какие углы называются вертикальными и каким свойством обладают вертикальные углы, какие прямые называются перпендикулярными. Уметь строить угол, смежный с данным углом, изображать вертикальные углы, объяснять, почему две прямые, перпендикулярные к третьей, не пересекаются, решать задачи типа 57, 58, 61, 64, 65, 69. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 8 | Перпендикулярные прямые. Построение прямых углов на местности, п.12, 13. | 1 | Перпендикулярные прямые. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 9 | Решение задач. | 1 |
|
Закрепить в процессе решения задач, полученные ЗУН, подготовиться к контрольной работе. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 10 | КОНТРОЛЬНАЯ РАБОТА №1 «Начальные геометрические сведения», п.1-13. | 1 |
| Уметь применять все изученные формулы и теоремы при решении задач | Контрольно-измерительный дифференцированный материал. |
|
|
|
| ГЛАВА II. ТРЕУГОЛЬНИКИ | 18 |
|
|
|
|
|
|
| §1. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ. |
|
|
|
|
|
|
| 11 | Треугольник, п.14. | 1 |
| Знать, что такое периметр треугольника, какие треугольники называются равными, формулировку и доказательство первого признака равенства треугольников. Уметь объяснить, какая фигура называется треугольником, и назвать его элементы, решать задачи типа 90, 92 – 95, 97. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 12 | Первый признак равенства треугольников, п.15. | 1 | Первый признак равенства треугольников. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 13 | Решение задач. | 1 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §2. МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА. |
|
|
|
|
|
|
| 14 | Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника, п.16, 17. | 1 | Перпендикуляр, медиана, высота, биссектриса | Уметь объяснить, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой, какие отрезки называются медианой, биссектрисой, высотой треугольника, какой треугольник называется равнобедренным, равносторонним; знать формулировку теоремы о перпендикуляре к прямой; знать и уметь доказывать теоремы о свойствах равнобедренного треугольника; уметь выполнять практические задания типа 100 – 104 и решать задачи типа 105, 107, 108, 112, 115, 117, 119. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 15 | Свойства равнобедренного треугольника, п.18. | 1 | Равнобедренный треугольник | Слайд-презентация, иллюстрация на доске.
|
|
|
| 16 | Решение задач. | 1 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §3. ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ. |
|
|
|
|
|
|
| 17 | Второй признак равенства треугольников, п.19. | 1 | Второй признак равенства треугольников | Знать формулировку и доказательство второго признака равенства треугольников. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 18 | Решение задач. | 1 |
| Знать формулировки и доказательства второго и третьего признаков равенства треугольников; уметь решать задачи типа 121 – 123, 125, 129, 132, 136, 137 – 139. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 19 | Третий признак равенства треугольников, п.20. | 1 | Третий признак равенства треугольников | Слайд-презентация, иллюстрация на доске.
|
|
|
| 20 | Решение задач. | 1 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §4. ЗАДАЧИ НА ПОСТРОЕНИЕ. |
|
|
|
|
|
|
| 21 | Окружность, п.21. | 1 |
| Знать определение окружности. Уметь объяснить, что такое центр, радиус, диаметр, хорда, дуга окружности, выполнять с помощью циркуля и линейки простейшие построения: отрезка, равного данному; биссектрисы данного угла; прямой, проходящей через данную точку и перпендикулярной к данной прямой; середины данного отрезка; применять простейшие построения при решении задач типа 148 – 151, 154, 155. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 22 | Построение циркулем и линейкой. Примеры задач на построение, п.22, 23. | 1 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
| 23 | Решение задач. | 1 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
| 24 25 26
| Решение задач. | 3 |
| Закрепить навыки в решении задач на применение признаков равенства треугольников, продолжить выработку навыков решения задач на построение с помощью циркуля и линейки. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 27 | КОНТРОЛЬНАЯ РАБОТА №2 «Треугольники», п.14-23. | 1 |
| Уметь применять весь изученный материал при решении задач. | Контрольно-измерительный дифференцированный материал. |
|
|
|
| ГЛАВА III. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. | 14 |
|
|
|
|
|
|
| §1. ПРИЗНАКИ ПАРАЛЛЕЛЬНО- СТИ ДВУХ ПРЯМЫХ. |
|
|
|
|
|
|
| 28 | Определение параллельных прямых, п.24. | 1 | Параллельные прямые | Знать определение параллельных прямых, названия углов, образующихся при пересечении двух прямых секущей, формулировки признаков параллельности прямых; понимать какие отрезки и лучи являются параллельными; уметь показать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности двух прямых и использовать их при решении задач типа 186 – 189, 191, 194.; уметь строить параллельные прямые при помощи чертежного угольника и линейки. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 29 30
| Признаки параллельности двух прямых, п.25. | 2 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
| 31 | Практические способы построения параллельных прямых, п.26. Решение задач. | 1 |
| Уметь строить параллельные прямые при помощи чертежного угольника и линейки, использовать теоретический материал при решении задач. | Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §2. АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. |
|
|
|
|
|
|
| 32 | Об аксиомах геометрии. Аксиома параллельных прямых, п.27,28. | 1 | аксиома | Знать аксиому параллельных прямых и следствия из нее, знать и уметь доказывать свойства параллельных прямых и применять их при решении задач типа 196, 198, 199, 203 – 205, 209. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 33 34
| Теорема об углах, образованных двумя параллельными прямыми и секущей, п.29. | 2 | Секущая | Слайд-презентация, иллюстрация на доске.
|
|
|
| 35 36 37
| Решение задач. | 3 |
| Закрепить навыки в решении задач. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 38 39 40 | Решение задач. | 3 |
| Уметь применять все изученные теоремы при решении задач. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 41 | КОНТРОЛЬНАЯ РАБОТА №3 «Параллельные прямые», п.24-29. | 1 |
| Контрольно-измерительный дифференцированный материал. |
|
|
|
| ГЛАВА IV СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. | 18 |
|
|
|
|
|
|
| §1. СУММА УГЛОВ ТРЕУГОЛЬНИКА. |
|
|
|
|
|
|
| 42 43
| Теорема о сумме углов треугольника. Остроугольный, прямоугольный и тупоугольный треугольники, п.30, 31. | 2 |
| Знать, какой угол называется внешним углом треугольника, какой треугольник называется остроугольным, тупоугольным, прямоугольным; уметь доказывать теорему о сумме углов треугольника и ее следствия, решать задачи типа 223 – 226, 228, 229, 234. | Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §2. СООТНОШЕНИЯ МЕЖДУ УГЛАМИ И СТОРОНАМИ ТРЕУГОЛЬНИКА. |
|
|
|
|
|
|
| 44 45
| Теорема о соотношениях между сторонами и углами треугольника, п.32. | 2 |
| Уметь доказывать теорему о соотношениях между сторонами и углами треугольника и следствия из нее, теорему о неравенстве треугольника, применять их при решении задач типа 236 – 240, 243, 244, 248, 249, 250. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 46 | Неравенство треугольника, п.33. | 1 | Неравенство треугольника | Слайд-презентация, иллюстрация на доске.
|
|
|
| 47 | КОНТРОЛЬНАЯ РАБОТА №4 «Сумма углов треугольника», п.30-33. | 1 |
| Уметь применять все изученные теоремы при решении задач. | Контрольно-измерительный дифференцированный материал. |
|
|
|
| §3. ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ. |
|
|
|
|
|
|
| 48 49
| Некоторые свойства прямоугольных треугольников, п.34. | 2 |
| Уметь доказывать свойства 10 – 30 прямоугольных треугольников; знать формулировки признаков равенства прямоугольных треугольников уметь их доказывать; уметь применять свойства и признаки при решении задач типа 254 – 256, 258, 260, 263, 265. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 50 51
| Признаки равенства прямоугольных треугольников. Угловой отражатель, п.35, 36. | 2 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
|
| §4. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ. |
|
|
|
|
|
|
| 52 53
| Расстояние от точки до прямой. Расстояние между параллельными прямыми, п.37. | 2 |
| Знать, какой отрезок называется наклонной, проведенной из данной точки к данной прямой, что называется расстоянием от точки до прямой и расстоянием между двумя параллельными прямыми; уметь доказывать, что перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой; теорему о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой; уметь строить треугольник по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трем сторонам; уметь решать задачи типа 271, 273, 277, 278(а), 283, 284, 288, 290, 291. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 54 55
| Построение треугольника по трем элементам. Решение задач, п.38. | 2 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
| 56 57 58
| Решение задач. | 3 |
| Закрепить навыки в решении задач. | Слайд-презентация, иллюстрация на доске.
|
|
|
| 59 | КОНТРОЛЬНАЯ РАБОТА №5 «Прямоугольный треугольник», п.34-38. | 1 |
| Уметь применять все изученные теоремы при решении задач. | Контрольно-измерительный дифференцированный материал. |
|
|
|
| ИТОГОВОЕ ПОВТОРЕНИЕ | 8 |
|
|
|
|
|
| 60 61
| Измерение отрезков и углов. Перпендикулярные прямые. | 2 |
| Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс геометрии 7класса). | Слайд-презентация, иллюстрация на доске.
|
|
|
| 62 63 64
| Треугольники. | 3 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
| 65 66
| Параллельные прямые. | 3 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
| 67 | Задачи на построение. | 2 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
| 68 | Итоговое занятие. | 1 |
| Слайд-презентация, иллюстрация на доске.
|
|
|
7 класс
| Контрольная работа № 1. |
| 1 вариант.
1). Три точки В, С, и D лежат на одной прямой. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС ?
2). Сумма вертикальных углов МОЕ и DOC, образованных при пересечении прямых МС и DE, равна 204 0 . Найдите угол МОD .
3). С помощью транспортира начертите угол, равный 780 , и проведите биссектрису смежного с ним угла.
| 2 вариант.
1). Три точки М, N и К лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МК ?
2). Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 0 . Найдите угол ВОD .
3). С помощью транспортира начертите угол, равный 1320 , и проведите биссектрису одного из смежных с ним углов.
|
|
Контрольная работа № 2. |
| 1 вариант.
1). На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что 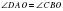 . . С    А O А O В D
2). Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  АDВ = АDВ = 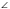 АDС . Докажите, что АВ = АС . АDС . Докажите, что АВ = АС .
3). В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2 . Найдите стороны треугольника.
| 2 вариант.
1). На рисунке 1 отрезки МЕ и РК точкой D делятся пополам. Докажите, что  КМD = КМD =  РЕD. РЕD.   ![]() М К М К
D
![]() Р Е Р Е
2). На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D и РК = РМ . Докажите, что луч DР – биссектриса угла МDК .
3). В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2 : 3 . Найдите стороны треугольника.
|
|
Контрольная работа № 3. |
| 1 вариант.
1). Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ // QF.
2). Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если 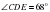 . .
3). На рисунке АС // ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка CD.   D D M ![]()  A B A B
C
| 2 вариант.
1). Отрезки МN и ЕF пересекаются в их середине Р. Докажите, что ЕN // МF.
2). Отрезок AD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне FD и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если  . .
3). На рисунке AB // DC, АВ = DC. Докажите, что точка О – середина отрезков АС и ВD.  В С В С О
А D |
| Контрольная работа № 4. |
| 1 вариант.
1). На рисунке:  . Найдите сторону АВ треугольника АВС. . Найдите сторону АВ треугольника АВС.   Е Е B М ![]() А А C D F
2). В треугольнике СDE точка М лежит на стороне СЕ, причём  - острый. Докажите, что DE DM. - острый. Докажите, что DE DM.
3). Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
| 2 вариант.
  1). На рисунке: 1). На рисунке:   . Найдите сторону АС треугольника АВС. . Найдите сторону АС треугольника АВС. ![]() Е М Е М A С
В D F
2). В треугольнике MNP точка К лежит на стороне MN, причём  - острый. Докажите , что КР - острый. Докажите , что КР
3). Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
|
|
Контрольная работа № 5. |
| 1 вариант.
1). В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NK в точке О, причём ОК = 9 см. Найдите расстояние от точки О до прямой МN.
2). Постройте прямоугольный треугольник по гипотенузе и острому углу.
3). Один из углов прямоугольного треугольника равен 60 0, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу .
| 2 вариант.
1). В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причём FC = 13 см. Найдите расстояние от точки F до прямой DE.
2). Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
3). В треугольнике АВС  , биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС. , биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС.
|
|
Итоговая контрольная работа |
| 1 вариант.
1). В равнобедренном треугольнике АВС с основанием АС угол В равен 42 0. Найдите два других угла треугольника АВС.
2). Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС  , ,  , АС = 10 см , СD , АС = 10 см , СD  АВ, DE АВ, DE  АС. Найдите АЕ. АС. Найдите АЕ.
4). В треугольнике МРК угол Р составляет 60 0 угла К, а угол М на 40 больше угла Р. Найдите угол Р. | 2 вариант.
1). В равнобедренном треугольнике АВС с основанием АС сумма углов А и С равна 156 0. Найдите углы треугольника АВС.
2). Величины смежных углов пропорциональны числам 4 и 11. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС  , ,  , ВС = 18 см , СК , ВС = 18 см , СК  АВ, КМ АВ, КМ  ВС. Найдите МВ. ВС. Найдите МВ.
4). В треугольнике BDE угол В составляет 30 0 угла D, а угол Е на 19 0 больше угла D. Найдите угол В. |
Темы творческих проектов:
-Чертежи, фигуры, линии и математические расчеты в кройке и шитье.
-Математические чертежи египетских пирамид.
-Треугольники Паскаля.
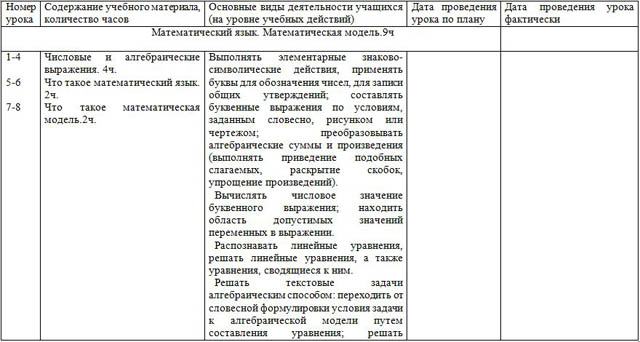

 Получите свидетельство
Получите свидетельство Вход
Вход










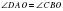 .
.
 А O
А O АDВ =
АDВ = 

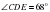 .
.
 D
D 








 Рабочая программа по математике (алгебра, 7 класс) (3.93 MB)
Рабочая программа по математике (алгебра, 7 класс) (3.93 MB)
 0
0 890
890 16
16 Нравится
0
Нравится
0









