Приложение №1
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ УЧИТЕЛЯ
Тема 1. ПРОЦЕНТЫ.
ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ (2 ч)
Сообщается история появления процентов; устраняются пробелы в знаниях по решению основных задач на проценты: а) нахождение процента от числа (величины); б) нахождение числа по его проценту; в) нахождение процента одного числа от другого. Актуализируются знания об арифметических и алгебраических приемах решения задач.
Метод обучения: лекция, беседа, объяснение.
Форма контроля: проверка самостоятельно решенных задач.
Занятие 1.
ЛЕКЦИЯ «ПРОЦЕНТЫ В ПРОШЛОМ И НАСТОЯЩЕМ»
Опорные сведения: нахождение процента от величины; нахождение величины по ее проценту; нахождение процента одной величины от другой.
Цели: сообщить историю появления процентов, привести примеры повседневного использования процентных вычислений в настоящее время; устранить пробелы в знаниях по решению основных задач на проценты: нахождение процента от величины, нахождение величины по ее проценту, нахождение процента одной величины от другой.
Метод обучения: лекция, объяснение, устные и письменные упражнения.
Формы контроля: проверка самостоятельно решенных задач.
Ход занятия
I. Лекция.
Проценты - одно из математических понятий, которые часто встречаются в повседневной жизни. Так, мы часто читаем или слышим, что, например, в выборах приняли участие 52,5 % избирателей, рейтинг победителя хит-парада равен 75 %, промышленное производство сократилось на 11,3 %, уровень инфляции составляет8 % в год, банк начисляет 12 % годовых, молоко содержит 3,2 % жира, материал содержит 60 % хлопка и 40 % полиэстера и т. д.
Слово «процент» происходит от латинского слова рrо сепtuт, что буквально означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотых долях. Это дает возможность упрощать расчеты и легко сравнивать части между собой и с целыми. Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян, которые пользовались шестидесятиричными дробями. Уже в клинописных табличках вавилонян содержатся задачи на расчет процентов. До нас дошли составленные вавилонянами таблицы процентов, которые позволяли быстро определять сумму процентных денег. Были известны проценты и в Индии. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т. е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов.
Денежные расчеты с процентами были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Даже римский сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.
В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы.
Впервые опубликовал таблицы для расчета процентов в 1584 г. Симон Стевин - инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий, в том числе - особой записи десятичных дробей.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Ныне процент - это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу).
Знак «%» происходит, как полагают, от итальянского слова сеп1о (сто), которое в процентных расчетах часто писалось сокращенно с1о. Отсюда путем дальнейшего упрощения в скорописи буквы I в наклонную черту произошел современный символ для обозначения процента.
Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 году в Париже была опубликована книга - руководство по коммерческой арифметике, где по ошибке наборщик вместо с1о напечатал %. Если мы говорим о предметах из некоторой заданной совокупности - деньгах, зарабатываемых в семье, материалах, продуктах питания, то процент, разумеется, 100 сотых частей самого себя. Поэтому обычно говорят, что она «принимается за 100 процентов». Если речь идет о проценте от данного числа, то это число и принимается за 100 %. Например, 1 % от зарплаты - это сотая часть зарплаты; 100 % зарплаты - это сто сотых частей зарплаты. Т. е. вся зарплата. Подоходный налог с зарплаты берется в размере 13 %, т. е. 13 сотых от зарплаты. Надпись «60 %» хлопка на этикетке
означает, что материал содержит 60 сотых хлопка, т. е. более чем на половину состоит из чистого хлопка. 3,2 % жира в молоке означает, что 3,2 сотых массы продукта составляет жир (или, другими словами, в каждых 100 граммах этого продукта содержится 3,2 грамма жира).
II. Устная работа.
Упражнения на закрепление понятия «процент». Предлагаются упражнения по переводу дроби в проценты, а проценты - в десятичные дроби.
1. Представьте данные десятичные дроби в процентах:
0,5 0,24 0,867 0,032 1,3 0,0081 15
0,01 154 3,2 20,5 0,7 10
2. Представьте проценты десятичными дробями:
2% 12,5% 2,67% 0,06% 32,8%
1000% 510% 0,5% 213% 0,1%
III. Повторение и закрепление изученного ранее.
Целесообразно напомнить основные сокращенные процентные отношения и записать в тетрадь.
100% = 1; 12,5 = 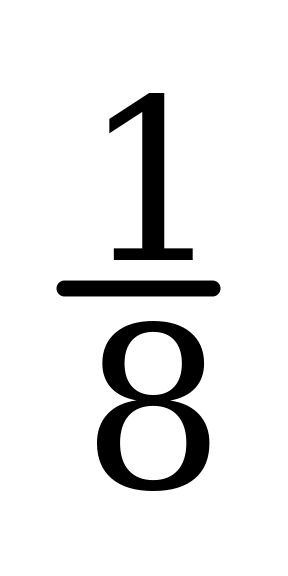 ; 5% =
; 5% = 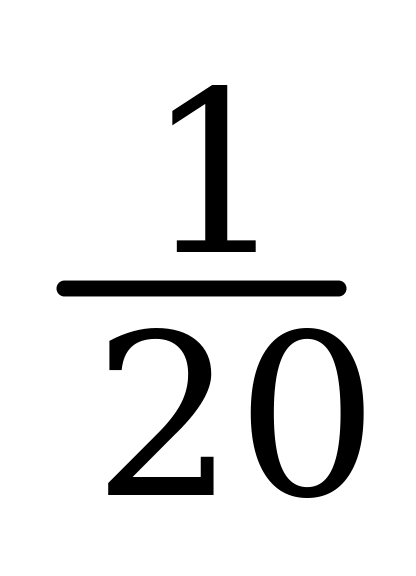 ;
;
50% = 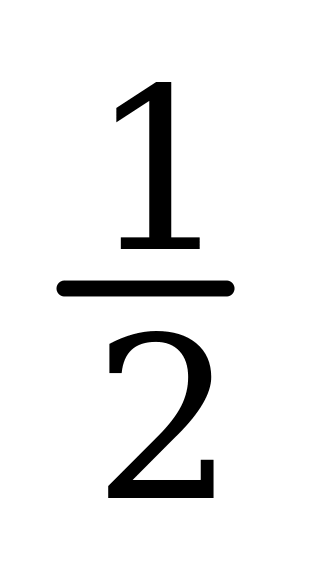 ; 200% = 2; 1% =
; 200% = 2; 1% = 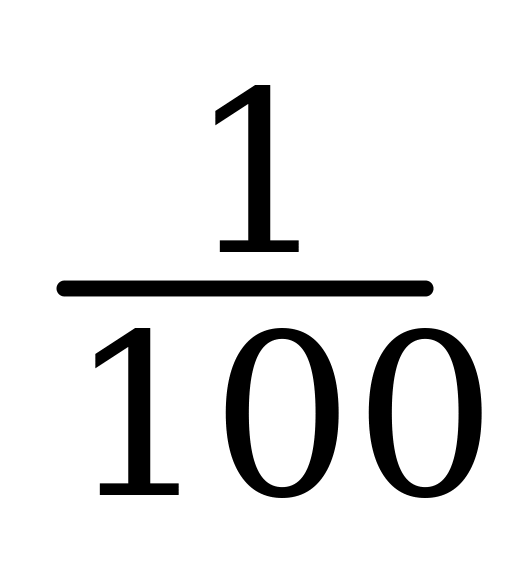 ;
;
25% = 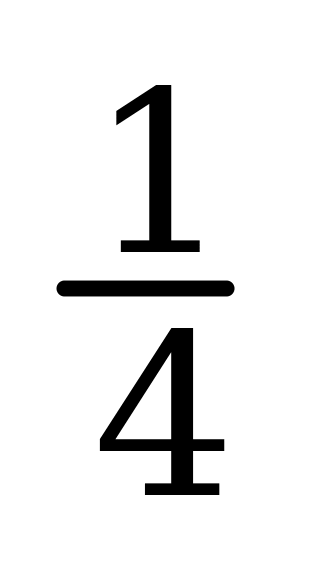 ; 10% =
; 10% = 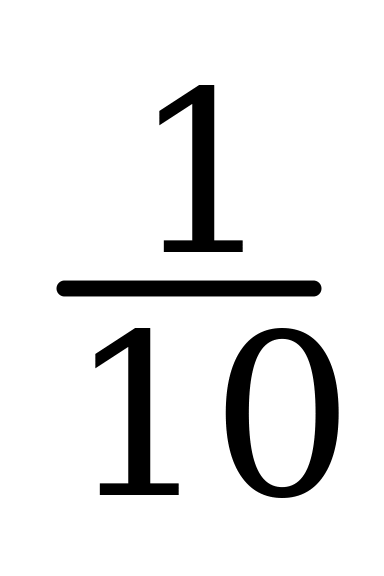
IV. Систематизация знаний.
Основные понятия, связанные с процентами:
Три основных действия:
1. Нахождение процентов данного числа.
Чтобы найти а % от в, надо в*0,01а.
П р и м е р. 40 % от 70 составляет: 70 * 0,4 = 28.
2. Нахождение числа по его процентам.
Если известно, что а % числа равно в, то х = в : 0,01а
П р и м е р. 3 % числа х составляют 150.
х =150: 0,03=5000.
3. Нахождение процентного отношения чисел.
Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100 %:
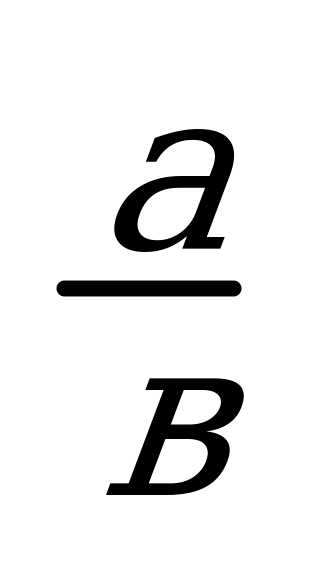 •100%.
•100%.
Пример. Сколько процентов составляет 150 от 600?
150 : 600•100% =25%
V. Решение основных задач на проценты.
1. Основные типы задач на проценты.
1) Одна величина больше (меньше) другой на р %.
а) Если а больше в на р %, то
а = в + 0,01 рв = в(1 + 0,01р).
б) Если а меньше в на р %, то
а = в - 0,01рв = в(1- 0,01р).
Пример. На сколько процентов надо увеличить число 80, чтобы получить 120?
Решение:
120 = 80 + 80 • 0,01р,
120 = 80(1+0,01 р)
120 : 80 = (1+0,01 р)
p= 50%
Ответ: 50%
Аналогично,
а) если а возросло на р %, то новое значение равно а(1 + 0,01р).
Пример. Увеличить число 60 на 20 %:
60 + 60*0,2 = 72 или 60(1 + 0,2) = 72;
б) если а уменьшили на р %, то новое значение равно:
а(1- 0,01р).
Пример. Число 72 уменьшили на 20 %:
72 – 72*0,2 = 57,6 или 72(1 - 0,2) = 57,6.
Объединив а) и б), запишем задачу в общем виде: увеличили число а на р %, а затем полученное уменьшили на р %
а(1 + 0,01р); а(1 + 0,01р)(1 - 0,01р) = а(1- (0,01р)2) (*)
Замечание. Результат не изменится, если увеличение (уменьшение) следует за уменьшением (увеличением).
Задача 1.
Цену товара снизили на 30 %, затем новую цену повысили на 30 %. Как изменилась цена товара?
Решение.
Пусть первоначальная цена товара а, тогда:
а - 0,3а = 0,7а - цена товара после снижения,
0,7а + 0,7а*0,3 = 0,91а- новая цена.
1,00-0,91 =0,09 или 9%.
Используя формулу (*) , получим :
а(1- (0,01р)2) = а ( 1 – 0,32) = 0,91 а
Ответ: цена снизилась на 9 %.
Задача 2.
Цену товара повысили на 20 %, затем новую цену снизили на 20 %. Как изменится цена товара?
Ответ: цена снизилась на 4 %.
3.Творческое задание. Решить задачу в общем виде.
Увеличили число а на р %. На сколько процентов надо уменьшить полученное число, чтобы получить а?
Решение:
а (1 + 0,01 р) - а (1 + 0,01 р)* 001 х = а
а (1 + 0,01 р) (1 -0,01 х)= а
1 -0,01 х =1/ (1 + 0,01 р)
0,01 х = 0,01 р / (1 + 0,01 р)
х = р / (1 + 0,01 р) (**)
VI. Итоги урока.
Вводный тест по теме «Проценты»
Домашнее задание. № 23, 24, 26 (Приложение 2)
Занятие 2
Цели: систематизировать знания учащихся, связанные с понятием процента; решение основных задач на проценты.
Метод обучения: беседа, объяснение, устные упражнения, письменные упражнения.
Форма контроля: проверка самостоятельно решенных задач.
Ход занятия
I. Проверка домашнего задания.
Фронтально проверить выполнение домашнего задания. Задания, вызвавшие затруднения, решить у доски.
П. Устная работа.
Тест – опрос. Установите истинность (ложность утверждения)
1) Верно ли:
а) 37% = 0,37
б) 290% = 2,9
в) 9% = 0,9
2) Верно ли:
а) 5% от 400 равно 20
б) 20% от 300 равно 6
в) 1% от 1 м равно 10 см
3) Найти число х:
а) 4% его равны 160; х = 400
б) 70% его равны 560; х = 800
в) 17% его равны 68; х = 400
4) Процентное отношение чисел:
а) 150 к 500 равно 30%
б) 7 к 10 равно 700%
в) 137 к 100 равно 137%
Таблица ответов:
| 1 | 2 | 3 | 4 |
| а | б | в | а | б | в | а | б | в | а | б | в |
| + | + | – | + | – | + | – | + | + | + | – | + |
Условные обозначения: + «Истинна, – «Ложь»
III. Решение задач.
Задача 1. После снижения цен на 5% стоимость одного метра ткани стала равна 380 рублей. Сколько стоил один метр ткани до снижения цены?
Решение.
Эту задачу удобно решить, составив пропорцию:
х рублей - 100%
380 рублей - 95%
х = 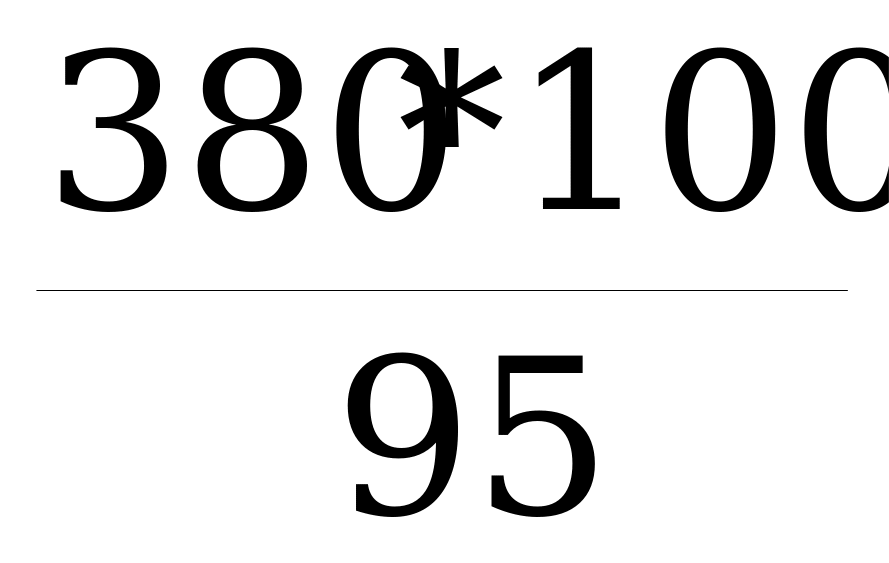
х = 400.
Ответ: До снижения цена 1 метра ткани составляла 400 рублей.
Задача 2. Цена товара после последовательных двух понижений на один и тот же процент уменьшилась со 125 рублей до 80 рублей. На сколько процентов цена снижалась каждый раз?
Решение:
в = 80, а = 125, n = 2. р -?
в = а (1- 0,01 р)
80 = 125(1-0,01 р)
Ответ: р = 20%
Задача 3. Цена на бензин в первом квартале увеличилась на 20 %, а во втором - а 30 %. На сколько процентов увеличилась цена на бензин за два квартала?
Решение :
Так как проценты находятся от величины, полученной после начисления процентов, то можно применить формулу сложных процентов.
Пусть цена бензина была х , тогда
в = х (1 + 0,2) (1 + 0,3) = 1,56 х
1,56 х – х = 0,56 х
Ответ: на 56 %.
Задача 4. Предприятие работало два года. В первый год выработка возросла на р %, во второй на 10% больше, чем в первый. Определить на сколько процентов увеличилась выработка за второй год, если за два года она увеличилась на 48,59 %.
%, во второй на 10% больше, чем в первый. Определить на сколько процентов увеличилась выработка за второй год, если за два года она увеличилась на 48,59 %.
Решение:
(1+ 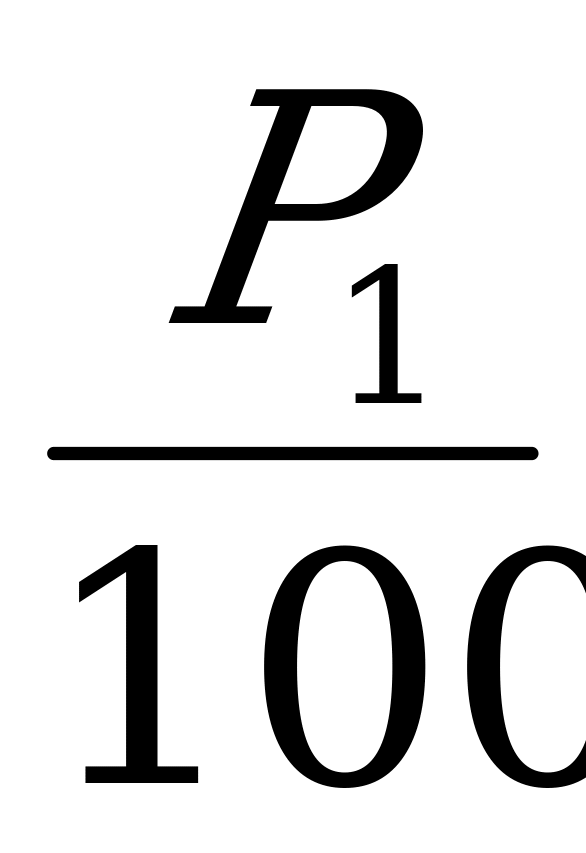 )(1+
)(1+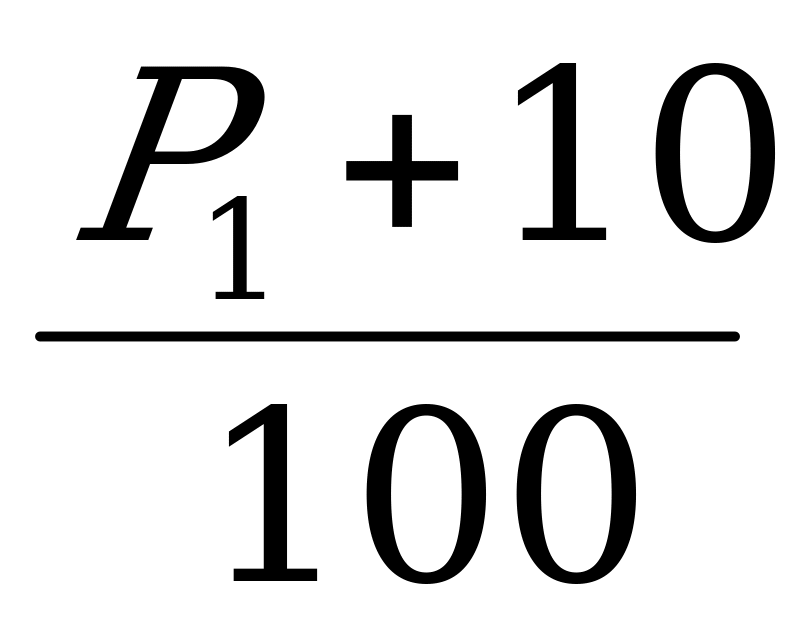 ) = 1,4859
) = 1,4859
р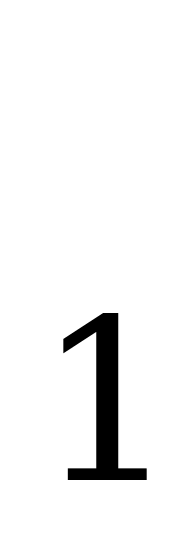 = 17%
= 17%
Ответ: за второй год выработка увеличилась на 27%.
Задача 5. Сберкасса начисляет 3% от суммы вклада. Через сколько лет сумма удвоится?
Решение:
в = 2 а
2 а = а (1+0,03)n
Ответ: n 23 года
23 года
 Задача 6. Вася прочитал в газете, что за последние 3 месяца цены на
Задача 6. Вася прочитал в газете, что за последние 3 месяца цены на
продукты питания росли в среднем на 10 % за каждый месяц. На
сколько процентов выросли цены за 3 месяца?
Решение :
Пусть х – новая цена,
х = (1 + 0,1)3
х = 1,331
1,331 – 1=0,331
Ответ: на 33,1 %.
Задача 7. Производительность труда на заводе снизилась на 20 %. На сколько процентов надо ее теперь повысить, чтобы достигнуть
первоначальной?
Решение :
Пусть х – первоначальная производительность,
р – процентные повышения,
х – 0,2 х = 0,8 х – производительность после понижения,
0,8 х + 0,8 х * 0,01 р – после повышения,
По условию 0,8 х + 0,8 х * 0,01 р = х,
р = 25.
Ответ: на 25 %.
Решить задачи №№ 41, 47 самостоятельно, с комментированием у доски.
Домашнее задание : №№ 45, 43, 48 (Приложение 2)
Тема 2 . Процентные вычисления в жизненных ситуациях ( 2 ч )
Цели : познакомить учащихся с понятиями «скидка» , «распродажа» , «бюджет» , «тарифы» , «пеня» , сформировать умение применять знания процентов в жизненных ситуациях, закрепить умение решать основные задачи на проценты.
Методы обучения : беседа, устные и письменные упражнения. Формы контроля: проверка самостоятельно решенных задач.
Занятие 3
РАСПРОДАЖА , ТАРИФЫ , ШТРАФЫ
Цели : добиться усвоения учащимися таких понятий, как скидка, распродажа, тарифы, штрафы, бюджет; отработать навыки решения основных задач на проценты.
Ход занятия
I. Устная работа.
Упражнения № 7, 11,15. (Приложение 2)
П . Объяснение нового материала.
Если при вычислении процентов на каждом следующем шаге исходят от величины, полученной на предыдущем шаге, то говорят о начислении сложных процентов (процентов на проценты). В этом случае применяется формула сложных процентов:
в = а(1+0,01р) п
где а - первоначальное значение величины;
в - новое значение величины;
р - количество процентов;
п - количество промежутков времени.
Если изменение происходит на разное число процентов, то формула выглядит так :
в = а(1+0,01р1) (1+0,01р2) (1+0,01р3)… (1+0,01рn)
Решение задач.
Задача 1. Зонт стоил 360 рублей. В ноябре цена зонта была снижена на 15%, а в декабре еще на 10%. Какой стала стоимость зонта в декабре?
Решение:
в = 360* (1 – 0,15) (1 – 0,1) = 360 * 0,765=275,4(р.)
Или другой способ:
Стоимость зонта в ноябре составляла 85 % от 360 р., т. е. 360 * 0,85 = 306(р.). Второе снижение цены происходило по отношению к новой цене зонта; теперь следует искать 90 % от 306 р., т. е. 306 * 0,9 = 275,4 (р.).
Ответ: 275 р. 40 к.
Дополнительный вопрос: На сколько процентов по отношению к первоначальной цене подешевел зонт?
Решение:
Найдем отношение последней цены к исходной и выразим его в процентах.
275,4 : 360 . 100 = 76,5 %
Получим 76,5 %. Значит, зонт подешевел на 100 – 76,5 = 23,5 %.
Ответ: 23,5%.
Задача 2. До снижения цен туфли стоили 960 рублей. Когда же цена на эти туфли снизилась, количество покупаемых туфель увеличилось на 20%, поэтому выручка от продажи увеличилась на 10%. На сколько рублей была снижена цена на туфли?
Решение:
Искомую величину снижения цены обозначим за х руб. Условие задачи удобно записать в виде таблицы.
|
| Цена (в рублях) | Количество проданных пар | Выручка (в рублях) |
| До снижения | 960 | п | 960 п |
| После снижения | 960 - х | 1,2 п | (960 - х)*1,2 п |
Зная, что выручка после снижения цены увеличилась на 10%, т. е. составляет 1,1 * 960 п, составим уравнение (960 - х) * 1,2 п = 1,1 * 960 п
Решим это уравнение:
(960 - х) * 1,2 п = 1,1 * 960 |:(1,2п)
960 - х = 880
х = 80
Ответ: Цена туфель снизилась на 80 рублей.
Задача 3. Заработок рабочего повысился на 20 %, а цены на продукты и другие товары снизились на 15 %. На сколько процентов рабочий теперь на свой заработок может купить больше продуктов и товаров, чем прежде?
Решение:
Примем для простоты вычислений прежний заработок рабочего за 10 р. и пусть он покупает только один какой-то продукт по 1 р. за килограмм, т. е. 10 кг. После повышения на 20 % заработок рабочего стал 12 р., а цена продукта после снижения цены на 15 % - 0,85 р. за 1 кг. Теперь рабочий может купить 12 : 0,85  14,1 (кг), т. е. на 4,1 : 10 = 0,41, т. е. на 41 % больше, чем прежде.
14,1 (кг), т. е. на 4,1 : 10 = 0,41, т. е. на 41 % больше, чем прежде.
Ответ: на 41 % больше.
Задача 4. Тарифы на проезд в наземном транспорте в г. N возросли с 2 до 10 р., соответственно с 2,5 до 15 р. – в городском метрополитене. Какие тарифы возросли больше?
Ответ: в метро.
Задача 5. Занятия ребенка в танцевальном кружке родители оплачивают в сбербанке, внося ежемесячно 350 р. Оплата должна производиться до 15 числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 5 % от суммы оплаты занятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на две недели?
Решение :
1) 350  0,05 = 17,5 (р) – пеня за каждый просроченный день
0,05 = 17,5 (р) – пеня за каждый просроченный день
2) 17,5  14 = 245 (р) – пеня за 2 недели
14 = 245 (р) – пеня за 2 недели
3) 350 + 245 = 595 (р) – придется заплатить
Ответ: 595 р.
Домашнее задание. № 59, 65 (Приложение 2) , составить задачи, используя жизненные ситуации.
Занятие 4
Банковские операции (1 ч)
При решении задач, связанных с банковскими расчетами необходимо подчеркнуть связь между задачами на проценты и геометрической прогрессией. Решение задач этой темы требует прочных вычислительных навыков, в своей работе учащиеся могут использовать калькулятор.
Цели: добиться усвоения учащимися понятия «простые проценты» , «сложные проценты» ; отработать навыки использования формулы при вычислении банковской ставки, суммы вклада, срока вклада. Метод обучения: выполнение тренировочных задач.
Ход занятия:
I. Проверка домашнего задания.
II. Рассказ учителя.
Простые проценты: Sn = S0 (1+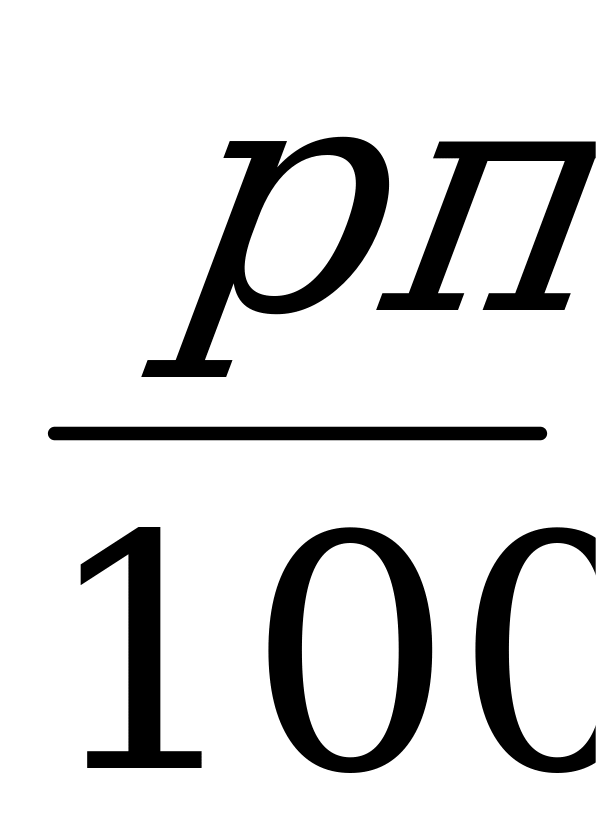 );
);
Увеличение вклада S0 по схеме простых процентов характеризуются тем , что суммы процентов течение всего срока хранения определяются исходя только из первоначальной суммы вклада S0 независимо от срока хранения и количества начисления процентов.
Сложные проценты : : Sn = S0 (1+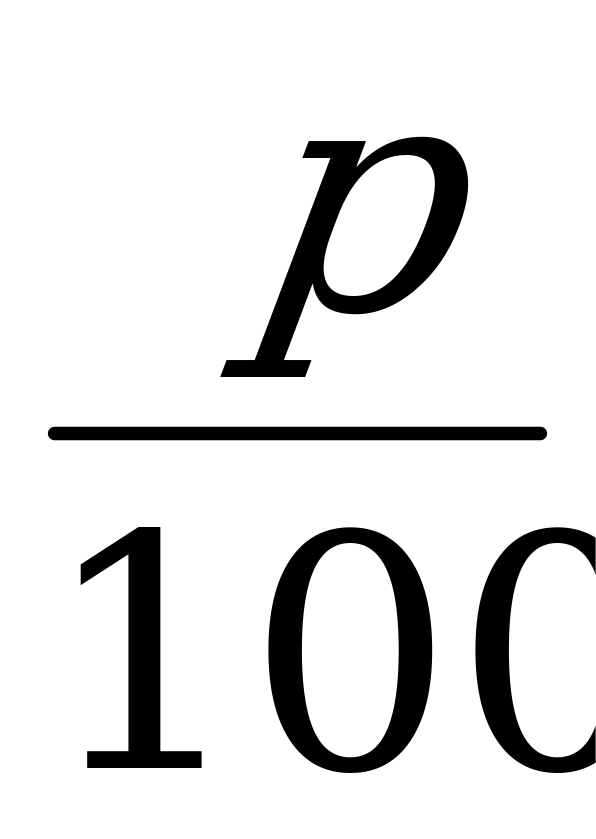 )п ;
)п ;
Рассмотрим другой способ расчета банка с вкладчиком. Он состоит в следующем : если вкладчик не снимает со счета сумму начисленных процентов, то эта сумма присоединяется к основному вкладу, а в конце следующего года банк будет начислять р % уже на новую, увеличенную сумму. Это означает , что банк теперь начисляет не только на основной вклад, S0 , но и на проценты, которые на него полагаются. Такой способ начисления «процентов на проценты» называют сложными процентами.
IП. Решение задач.
Задача 1. В банке открыт счет 50000 рублей под 10% годовых. Какой доход будет через 3 года?
Решение:
в = 50000 (1 + 0,1)3
в = 66550
66 550 – 50 000 = 16 550
Ответ: 16550.
Задача 2. В банк поместили некоторую сумму и через два года она выросла на 512,5 рублей. Сколько денег положили в банк, если вкладчикам выплачивается 5% годовых?
Решение:
в = а +512,5
а +512,5 = а (1+0,05)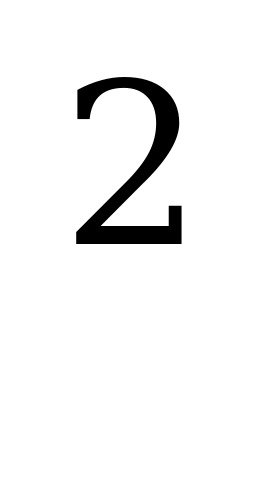
Ответ: а = 5000 руб.
Задача 3. Вкладчик поместил определенную сумму в банке под проценты. После первого начисления процентов он добавил к получившемуся вкладу сумму, равную половине исходной. После второго начисления процентов доход составил 76%. Каков был процент в банке?
Решение:
Пусть х рублей вкладчик положил в банк. Пусть процент вклада в банке составляет у%. После первого начисления вклад составил
х+ 0,01ух= х(1+0,01у) рублей.
Добавим сумму равную половине исходной: х(1+0,01у) + 0,5х = х(1,5+0,01у).
Второе начисление процентов:
х(1,5+0,01у) +0,01у(х(1,5+0,01у)) = х(1,5+0,01у)(1+0,01у)
Согласно условию задачи получаем уравнение:
х(1,5+0,01у)(1+0,01у) = 1,76х
(1,5+0,01у)(1+0,01у) = 1,76
1,5 + 0,015у + 0,01у + 0,0001у2=1,76
0,0001у2 +0,025у -0,26 = 0 *10000
у2+250у -2600 =0
Д= 1252 +2600 = 18225 =135
у= -125+135=10%
Ответ: 10%
Задача 4. Вкладчик положил в банк деньги под 10%. После начисления процентов некоторую сумму он изъял, а остаток оставил в банке. После второго начисления процентов оказалось, что образовавшаяся на счету сумма на 1% меньше исходной величины вклада. Сколько процентов от исходной суммы было изъято вкладчиком после первого начисления процентов?
Решение:
Пусть х рублей вкладчик положил в банк. После первого начисления вклад составил 1,1х рублей. Изъятая сумма составила у рублей, тогда оставшаяся на счету сумма равна 1,1х – у рублей. После второго начисления процентов вклад составляет 1,1(1,1х – у) = 1,21х – 1,1у. Согласно условию задачи получаем уравнение:
1,21х – 1,1у = 0,99х
1,21х – 0,99х = 1,1у
0,22х = 1,1у
у= 0,2х
Значит, изъятая сумма составляет 20% от вклада.
Ответ: 20%
Задачи для самостоятельного решения:
Задача 5. По срочному вкладу банк выплачивает 7% за срок хранения . На данный вклад был открыт счет, и после первого начисления процентов к нему была добавлена некоторая сумма. Однако банк понизил ставку до 5% за период хранения, и поэтому после второго начисления процентов доход по вкладу составил 30,2%. Сколько процентов первоначальной суммы было добавлено к вкладу?
Ответ: 17%
Задача 6. Банк обещает вкладчикам удвоить их сбережения за 5 лет, если они воспользуются вкладом «Накопление» с годовой процентной ставкой 16%. Проверьте, выполнит ли банк свое обязательство.
Ответ: да.
Домашнее задание: задания для выбора из дидактического материала. (Приложение 2)
Тема 3. ЗАДАЧИ НА СМЕСИ , СПЛАВЫ , КОНЦЕНТРАЦИЮ ( 2 ч)
Занятие 5
Цели: сформировать умение работать с законом сохранения массы; обеспечить усвоение учащимися понятий концентрации вещества, процентного раствора; обобщить полученные знания при решении задач на проценты.
Форма занятия: комбинированное занятие.
Методы обучения: рассказ, объяснение, практическая работа.
Формы контроля: проверка самостоятельно решенных задач.
Ход занятия
I. Проверка домашнего задания.
II. Рассказ учителя.
Тип задач на составление уравнений и систем уравнений – задачи на сплавы и смеси, решение которых связано с понятиями «концентрация», «процентное содержание», «проба», «влажность».
При решении задач данного типа используются следующие допущения:
1. Всегда выполняется «Закон сохранения объема или массы»:
если два раствора (сплава) соединяют в «новый» раствор (сплав),
то выполняются равенства:
V = V1 + V2 - сохраняется объем;
т =m1+ т2~ закон сохранения массы.
Данный закон выполняется и для отдельных составляющих частей
(компонентов) сплава (раствора).
3. При соединении растворов и сплавов не учитываются химические взаимодействия их отдельных компонентов.
Концентрация - это число, показывающее, сколько процентов от всей смеси составляет растворимое вещество. Если масса смеси т кг, масса растворимого вещества а кг, концентрация р %, то между этими величинами существует следующая зависимость: 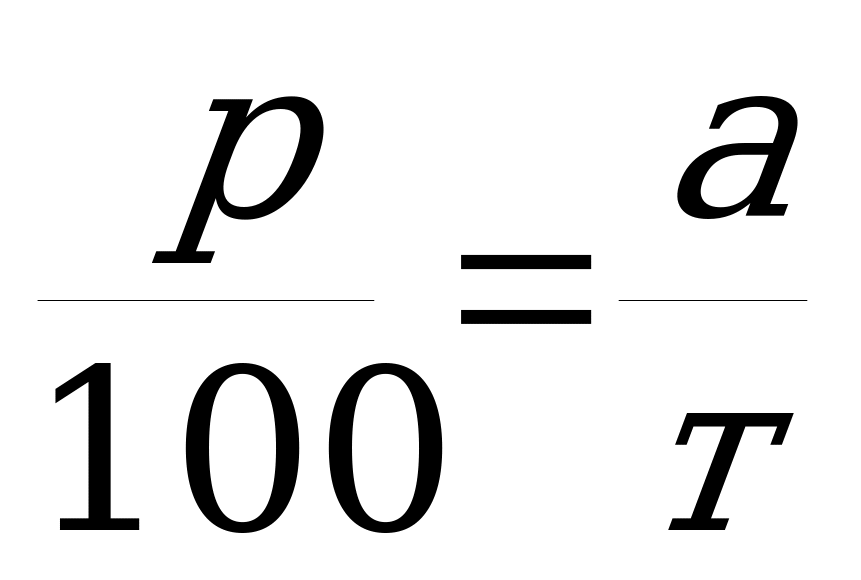 ; 100*а = т*р.
; 100*а = т*р.
Пример работы над задачами с понятием концентрации:
| Масса смеси | Масса растворимого вещества | Концентрация |
| т кг | а кг | р % |
| 10 | 1 | 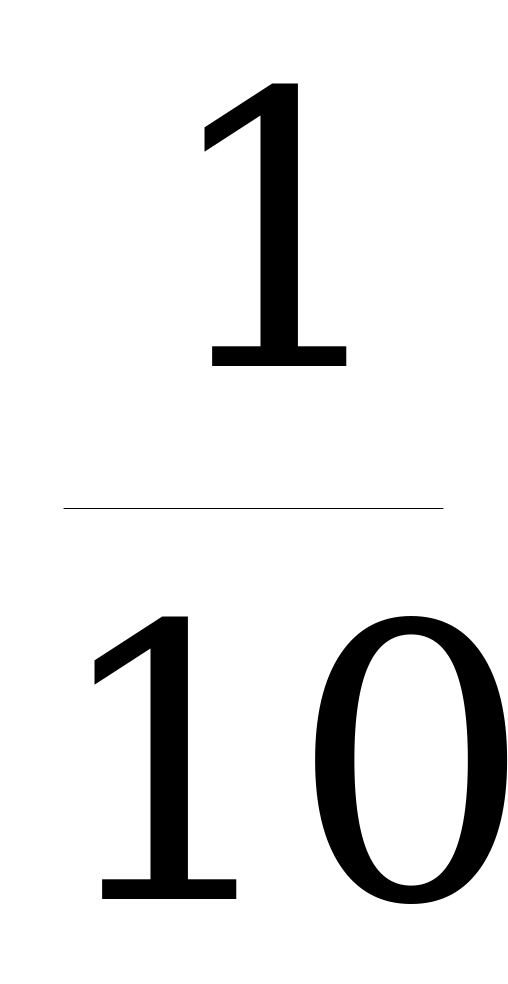 = 10% = 10%
|
| 5 | 2 | 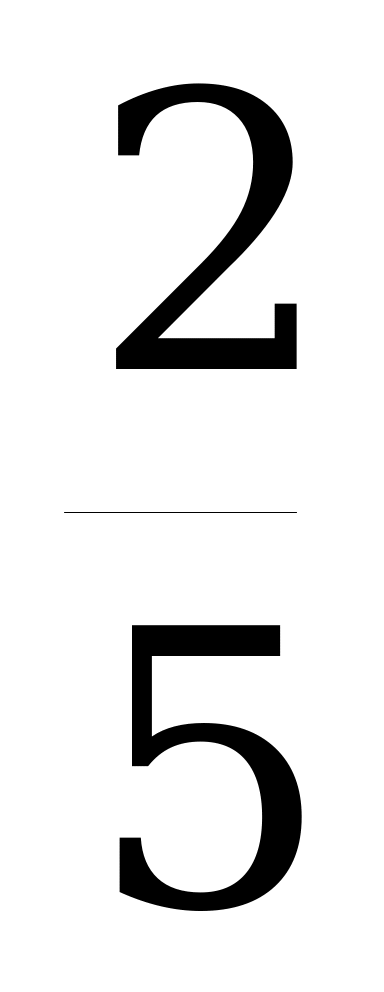 = 0,4 = 40% = 0,4 = 40%
|
| 4 | 0,5 | 0,5:4 =0,125=12,5% |
| mc | тв | тв / mc = к |
После получения этой формулы задачи на растворы будут осознанно решаться учащимися на основе соотношения:
тв =k*mc; mc = тв:к;  .
.
Процентное содержание вещества в растворе, иногда называют %-м раствором, например, 15%-й раствор соли.
1. Сколько кг соли в 10 кг соленой воды, если %-е содержание соли 15%?
Решение:
10∙0,15 = 1,5(кг).
Ответ: 1,5 кг.
Процентное содержание вещества в сплаве – это часть, которую составляет вес данного вещества от веса всего сплава.
2. Концентрация серебра в сплаве 300 г составляет 87%.
Это означает, что чистого серебра в сплаве 300∙0,87 = 261 г.
3. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение:
1) 10 + 15 = 25(кг) - сплав;
2) 10 : 25 ∙ 100% = 40% - процентное содержание олова в сплаве.
3) 15 : 25 ∙ 100% = 60% - процентное содержание цинка в сплаве.
Ответ: 40%, 60%.
Задача 1. Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 % раствор?
Решение:
Пусть х - количество воды, которое надо добавить. Новое количество раствора - (50 + х) г. Количество соли в исходном растворе 50  0,08 г. Количество соли в новом растворе составляет 5 % от (50+х)г, т. е.
0,08 г. Количество соли в новом растворе составляет 5 % от (50+х)г, т. е.
0,05(50+ х)
Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс по соли».
50  0,08 = 0,05(50+х),
0,08 = 0,05(50+х),
50 8 = 5(50+х),
8 = 5(50+х),
80 = 50+х,
х = 30.
Ответ: 30 г.
Задача 2. Сколько граммов 30 %-го раствора надо добавить к 80 г 12 %-го раствора этой же соли, чтобы получить 20 %-й раствор соли?
Решение:
Пусть надо добавить х г 30 % раствора соли. Получится (80 + х) г 20 % раствора. В 80 г 12 % раствора содержится 80  0,12 г соли , 0,3*х г соли - в х г 30 % раствора, 0,2(80 + х) г соли - в (80 + х) г 20 % раствора.
0,12 г соли , 0,3*х г соли - в х г 30 % раствора, 0,2(80 + х) г соли - в (80 + х) г 20 % раствора.
Получаем уравнение:
0,3х + 0,12  80 = 0,2(80 + х)- это и есть «баланс по соли».
80 = 0,2(80 + х)- это и есть «баланс по соли».
0,3х + 9,6=16 + 0,2х,
0,3х - 0,2х = 16 - 9,6,
0,1х = 6,4,
х = 64.
Ответ: 64 г.
Задача 3. Имеется два сплава, в одном из которых содержится 40%, а в другом 20% серебра. Сколько кг второго слава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Решение (с помощью уравнения):
Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. Тогда получим (20 + х) кг нового сплава. В 20 кг первого сплава содержится
0,4 ∙ 20 = 8 (кг) серебра, а в (20+ х) кг нового сплава содержится 0, 32∙(20+ х) кг серебра. Составим уравнение: 8+0,2 х = 0,32(20+ х), х =13 1/3.
Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
Задача 4. Имеется два куска сплава олова и свинца, содержащие 60 % и 40 % олова. По сколько граммов от каждого куска надо взять, чтобы получить 600 г сплава, содержащего 45 % олова?
Решение:
Пусть масса куска, взятого от первого сплава т1 г, тогда масса куска от второго сплава будет 600 – т1, составим уравнение
т1 0,6 + (600 - m1) 0,4 = 600  0,45,
0,45,
6 т1 + 2400 - 4 т1= 2700,
20 т1 = 3000,
т1= 150,
600 – т1 = 450,
т2 =450.
Ответ: 150 г; 450 г.
Задача 5. При смешивании 5%-ного раствора кислоты с 40%-ным раствором кислоты получили 140 г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?
Решение (с помощью системы уравнений):
Проследим за содержанием кислоты в растворах. Возьмем для смешивания х г 5%-ного раствора кислоты (или 0,05 х г) и у г 40%-ного раствора (или 0,4 у г). Так как в 140 г нового раствора кислоты стало содержаться 30%, т. е. 0,3∙140 г, то получаем следующее уравнение 0,05 х + 0,4 у = 0,3∙140. Кроме того х + у = 140.
Таким образом, приходим к следующей системе уравнений:
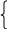
0,05 х + 40 у = 30∙140,
х + у = 140.
Из этой системы находим х = 40, у = 100. Итак, 5%-ного раствора кислоты следует взять 40 г, а 40%-ного раствора – 100 г.
Ответ: 40 г, 100 г.
Старинный способ решения
Таким способом можно решать задачи на смешивание (сплавление) любого числа веществ. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л. Ф. Магницкого. Данный способ позволяет получить правильный ответ.
Решим предыдущую задачу старинным способом. Друг под другом пишутся содержания кислот имеющихся растворов, слева от них и примерно посередине – содержание кислоты в растворе, который должен получиться после смешивания. Соединив написанные числа черточками, получим такую схему:
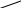 5
5
3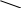 0
0
40
Рассмотрим пары 30 и 5; 30 и 40. В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей черточки. Получится такая схема:
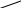 5 10
5 10
3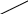
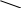
 0
0
40 25
Из нее делается заключение, что 5%-ного раствора следует взять 10 частей, а 40%-ного – 25 частей (140 : 35 = 4 г приходится на одну часть), т. е. для получения 140 г 30%-ного раствора нужно взять 5%-ного раствора 40 г, а 40%-ного – 100 г.
Ответ: 40 г, 100 г.
Задача 6. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение (старинным способом):
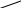
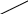
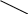 10 3
10 3
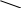 8
8
5 2
Таким образом 15 л – это 3 части, 15 : 3 = 5 л приходится на одну часть, тогда 5 ∙ 2 = 10 л добавили 5%-ного раствора.
Ответ: 10 л.
Домашнее задание. Задачи из приложения 4 (задания из вариантов ЕГЭ)
Занятие 6
Цель: углубить и систематизировать знания учащихся при решении задач на «смеси» и «сплавы».
Ход занятия
Решение задач.
Задача 1. Даны два куска с различным содержанием олова. Первый, массой 300 г, содержит 20 % олова. Второй, массой 200 г, содержит 40 % олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков.
Ответ: 28%.
Учащиеся решают самостоятельно, один из учеников комментирует решение.
Задача 2 . Сплав олова с медью весом 12 кг содержит 45% меди. Сколько чистого олова надо добавить, чтобы получить сплав, содержащий 40% меди.
Решение:
|
| 1 сплав | олово | 2 сплав |
| Масса сплава | 12 кг | х | 12+х |
| % содержания меди | 45% |
| 40% |
| % содержания олова | 55% | 100% | 60% |
| Масса олова | 12*0,55=6,6 | х | (12+х)*0,6 |
6,6 + х = (12+х)*0,6
6,6 + х = 7,2 +0,6х
0,4х = 0,6
х = 1,5 кг
Ответ: 1,5 кг олова нужно добавить
Задача 3. Морская вода содержит 8% по весу соли. Сколько килограммов пресной воды нужно добавить к 30 кг морской воды, чтобы содержание соли в последней составило 5%?
Решение:
|
| 1 состав | Пресная вода | 2 состав |
| Масса морской воды | 30 кг | х кг | 30 +х |
| % содержания соли | 8% | 0% | 5% |
| Масса соли | 30*0.08 | х*0 | (30+х)*0,05 |
30*0,08 = (30+х)*0,05
2,4 = 1,5 + 0,05х
0,05х = 0,9
х = 18 кг
Ответ: 18 кг пресной воды
Задача 4. Из 38 тонн сырья второго сорта, содержащего 25% примесей после очистки получается 30 тонн сырья первого сорта. Каков процент примесей в сырье первого сорта?
Решение:
| | 2 сорт | примеси | 1 сорт |
| Масса сырья | 38 т | 8 т | 30 т |
| % содержания примесей | 25% | 100% | х% |
| Масса примесей | 38*0,25 | 8 | 30*0,01х |
38*0,25 – 8 = 30*0,01х
9,5 – 8 = 0,3х
0,3х = 1,5
х = 5%
Ответ: 5% примесей
Задача 5. Определить сколько килограммов сухарей с влажностью 15% можно получить из 255 кг хлеба влажностью 45%?
Решение:
|
| хлеб | вода | сухари |
| Масса (кг) | 255 | х | 255-х |
| % влажности | 45 | 100 | 15 |
| Масса воды | 255*0,45 | х | ( 255-х)*0,15 |
255*0,45 – х = (255-х)*0,15
114,75 – х = 38,25 – 0,15х
х – 0,15х = 114,75 – 38,25
0,85х = 76,5
х = 90 кг воды
255 – 90 = 165 кг сухарей
Ответ: 165 кг сухарей
Задача 6. Свежие грибы содержат по массе 90% воды, а сухие – 20%. Сколько надо собрать свежих грибов, чтобы из них получить 4,5 кг сухих грибов?
Решение:
|
| Свежие грибы | Вода | Сухие грибы |
| Масса (кг) | х+4,5 | х | 4,5 |
| % содержание воды | 90 | 100 | 20 |
| Масса воды | (х+4,5)*0,9 | х | 4,5*0,2 |
(х+4,5)*0,9 = х + 4,5*0,2
0,9х + 4,05 = х + 0,9
х – 0,9х = 4,05 – 0,9
0,1х = 3,15
х = 3,15 : 0,1
х = 31,5 (кг) - воды
31,5 + 4,5 = 36 (кг) - свежих грибов
Ответ: 36 кг свежих грибов
Задача 7. Имеется два сплава золота и серебра. В одном эти металлы находятся в отношении 2:3, в другом 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором эти металлы были бы в отношении 5:11?
Решение:
1 способ :
2 + 3 = 5 (частей ) – всего в 1 сплаве
3 + 7 = 10 (частей ) – всего во 2 сплаве
5 + 11 = 16 (частей ) – всего в 3 сплаве
|
| I | II | новый |
Сплав | х | 8 - х | 8 |
Золото | 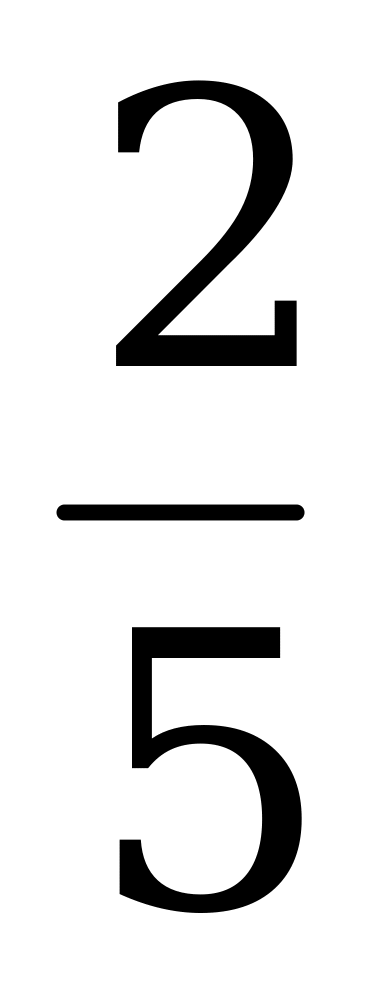
| 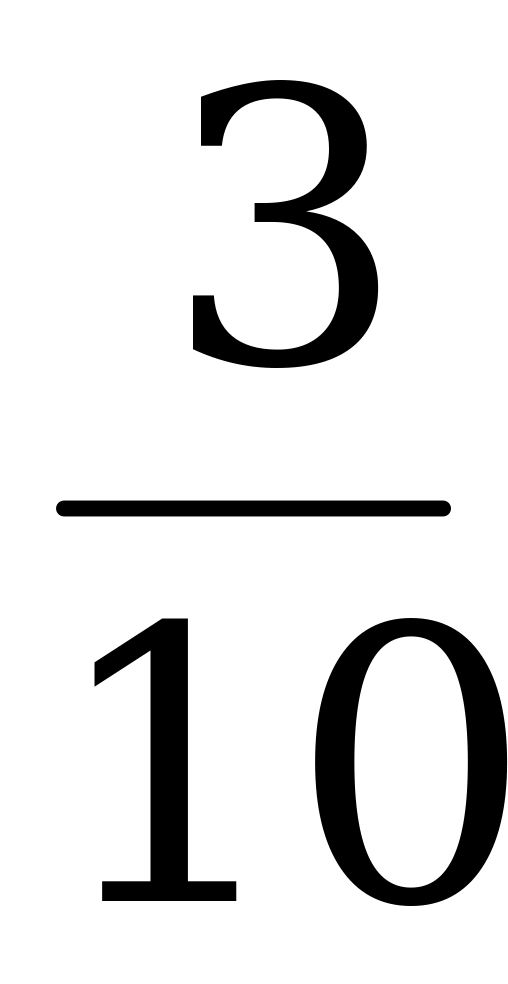
| 
|
Масса |  х х
| 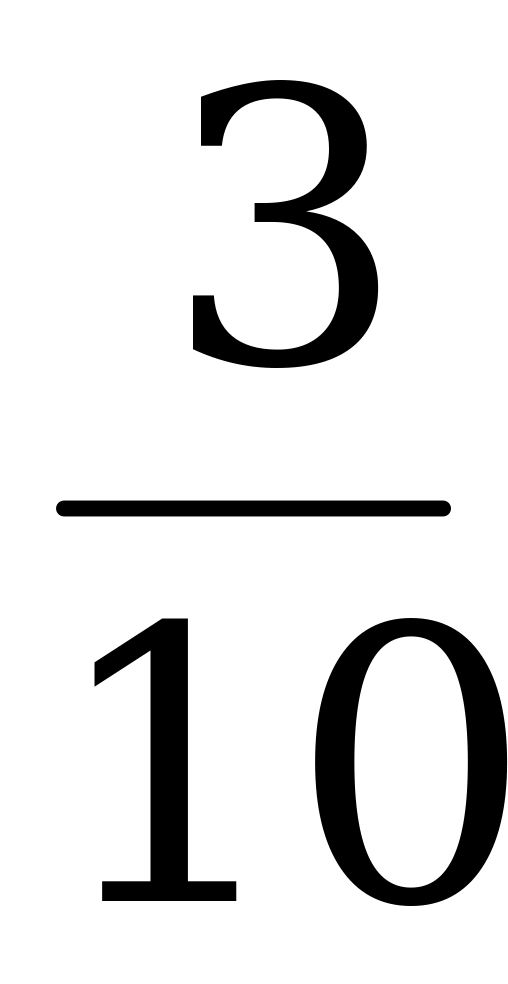 (8 – х) (8 – х)
|  *8 *8
|
 х +
х +  (8-х) = 8 *
(8-х) = 8 * 
х = 1
2 способ :
| Сплав | Масса взятого сплава, кг | M золота, кг | M серебра, кг |
| I | x |  х = 0,4х х = 0,4х
|  х = 0,6х х = 0,6х |
| II | 8 - x | 3(8 – x)= 0,3(8-x) 10 | 7(8 – x) = 0,7(8-x) 10 |
| Новый | 8 |
|
|
Золото 2x + 3(8 – x)
5 10 = 5 ,
Серебро 3x + 7(8 – x) 11 или  =
= 
10
4x + 3(8 –x) = 5 ,
6x + 7(8 – x) 11
4x + 24 – 3x = 5 ,
6x + 56 – 7x 11
x + 24 = 5 ,
56 – x 11
11x + 264 = 280 – 5x,
16x = 16,
x = 1, значит, от первого сплава взяли 1 кг, от второго 8 – x = 8 – 1 = 7 (кг)
3 способ :
З : С = 2 : 3
З : С = 3 : 7
х кг у кг
З : С = 5 : 11
 х + у = 1,
х + у = 1,
0,4 х + 0,3 у = 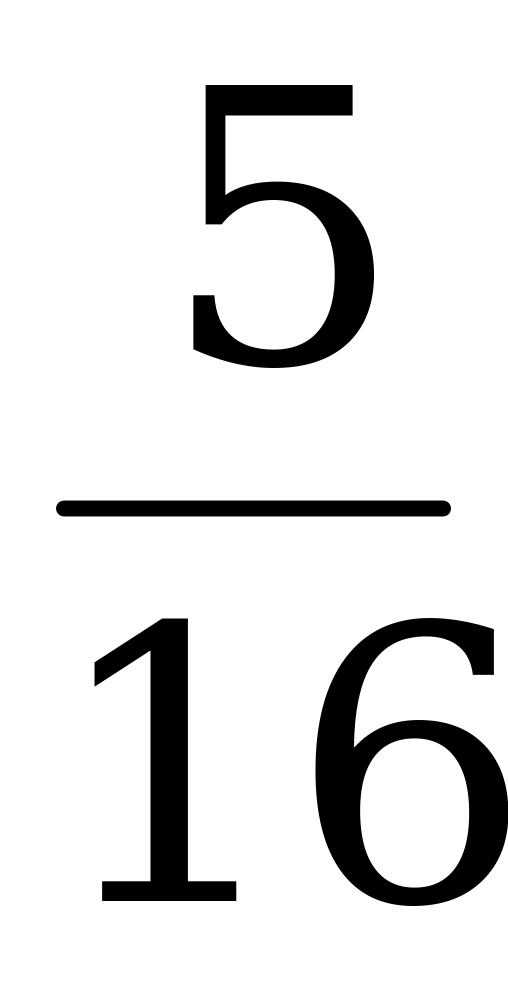 ;
;
Решая её, получаем х =1, у = 7
Ответ: золота – 1 кг, серебра – 7 кг.
Задача для самостоятельного решения:
1. В свежих яблоках 80% воды, а в сушеных 20%. На сколько процентов уменьшается масса яблок при сушке? Ответ: 75%
Домашнее задание. № 107, 109, 114. (Приложение 2)
Занятие 7
Цели: углубить и систематизировать знания учащихся.
Метод обучения: беседа.
Формы контроля: проверка самостоятельно решенных задач.
Ход занятия
I. Устная работа.
1. В классе присутствует 60% всех учащихся. Сколько процентов учащихся отсутствует?
1. Выразите в процентах ¼ всех жителей города.
3. Найдите 16% от 20000 рублей.
4. Сколько будет, если 20000 руб. увеличить на 16%?
5.Сколько процентов составляют 400 руб. от 200 руб.?
6. 20% некоторой суммы составляют 100 рублей. Какая это сумма?
П. Решение задач.
Задача 1. (на производительность).
В бассейн проведена труба. Вследствие засорения ее приток воды уменьшился на 60 %. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна ?
Решение:
100 % - 60 % = 40 % или 0,4 - такую часть составляет оставшийся приток воды;
1 : 0,4 = 2,5 (раза) - во столько раз увеличится время, необходимое для наполнения бассейна, т. е. увеличится на 150 %.
Ответ: на 150 %.
Задача 2. Одной машинистке на перепечатку рукописи требуется на 12 ч больше, чем другой. Если 25% рукописи перепечатает первая машинистка, а затем к ней присоединится вторая машинистка, то на перепечатку рукописи им понадобиться 35 ч, считая от момента начала работы первой машинистки. За сколько часов могла бы перепечатать рукопись каждая машинистка, работая отдельно?
Решение:
Пусть на перепечатку рукописи первой машинистке требуется 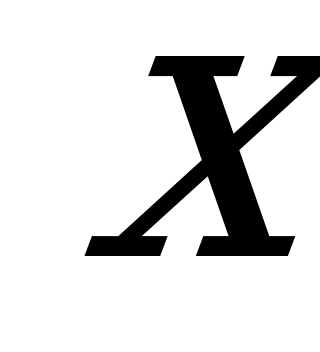 ч, тогда второй потребуется
ч, тогда второй потребуется 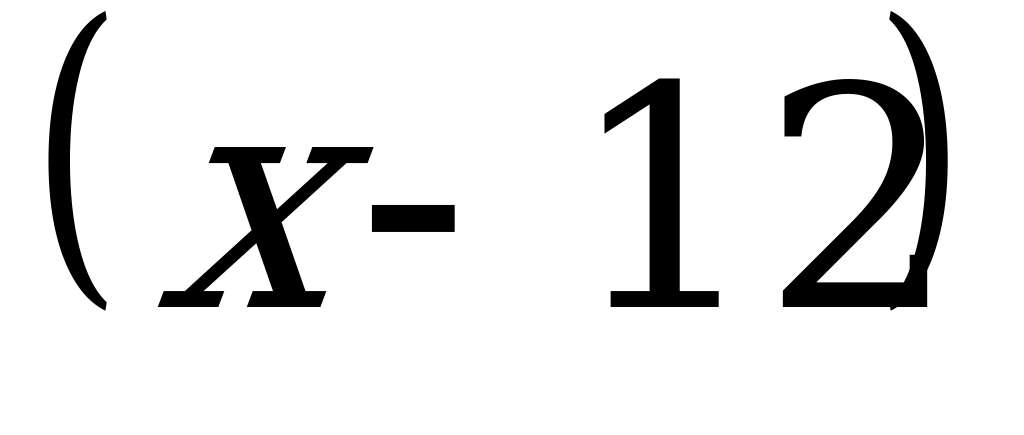 ч. На перепечатку 25% рукописи первая машинистка затратит
ч. На перепечатку 25% рукописи первая машинистка затратит 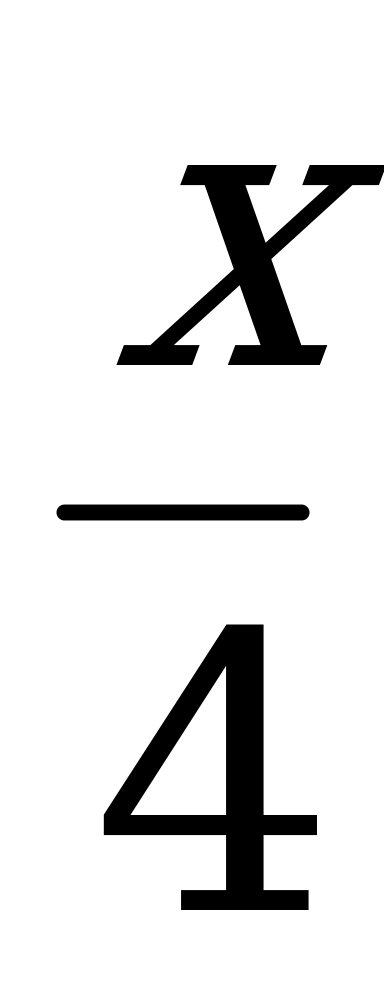 ч. Выясним теперь, сколько времени потребуется двум машинисткам на перепечатку оставшихся 75% рукописи. Первая машинистка перепечатывает за один час
ч. Выясним теперь, сколько времени потребуется двум машинисткам на перепечатку оставшихся 75% рукописи. Первая машинистка перепечатывает за один час 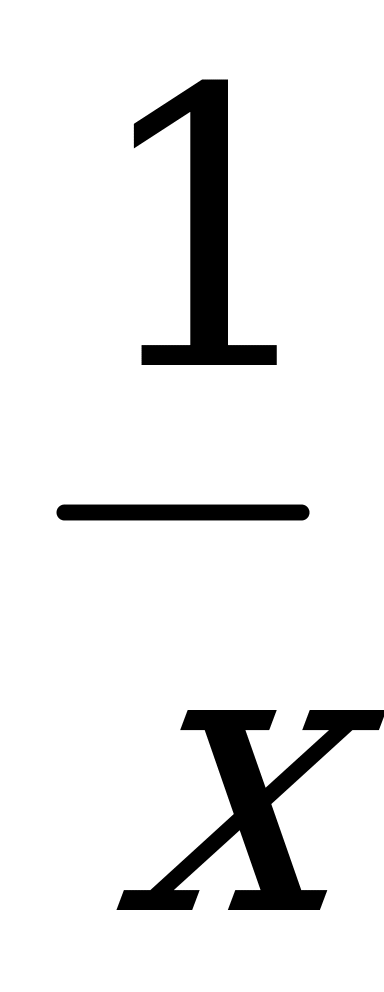 часть рукописи, вторая –
часть рукописи, вторая – 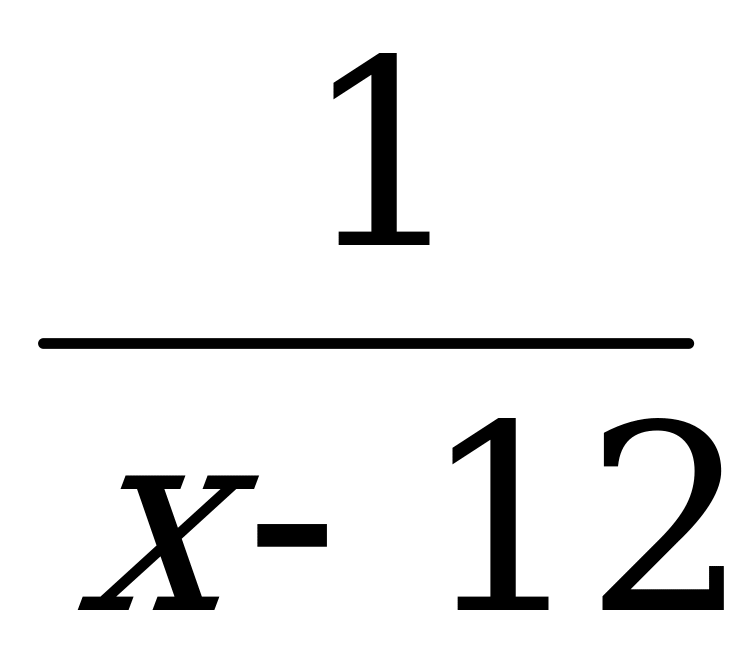 часть рукописи, а вместе за час они перепечатывают
часть рукописи, а вместе за час они перепечатывают 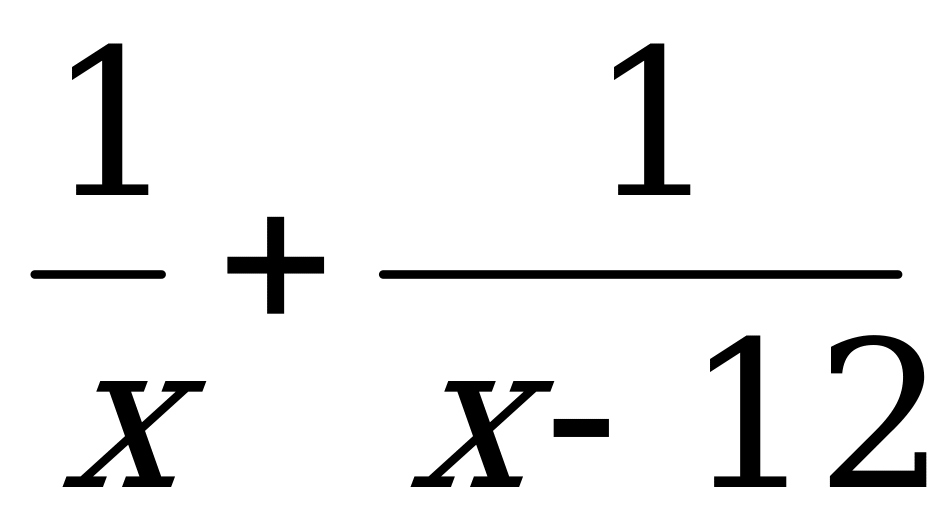 часть рукописи. На перепечатку
часть рукописи. На перепечатку 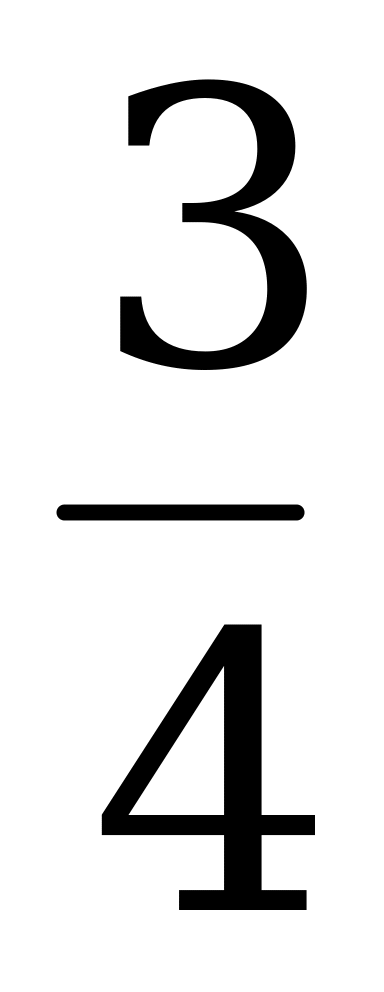 рукописи им потребуется
рукописи им потребуется 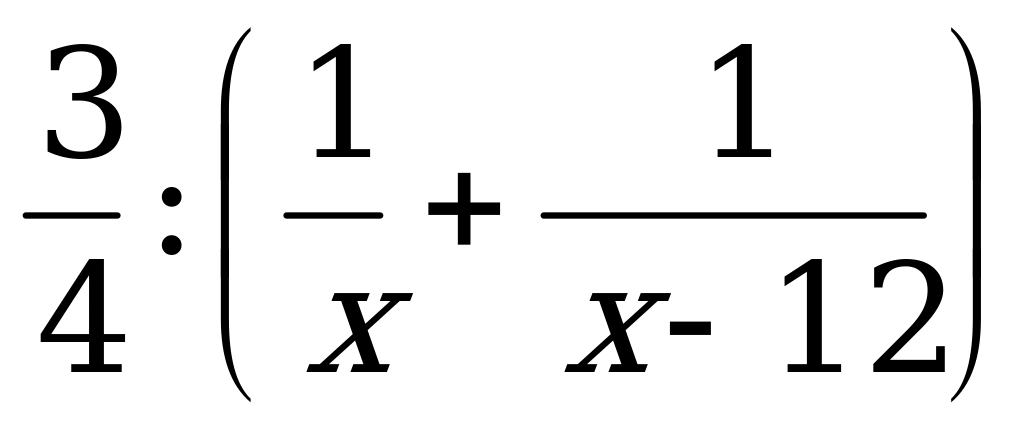 ч, т.е.
ч, т.е. 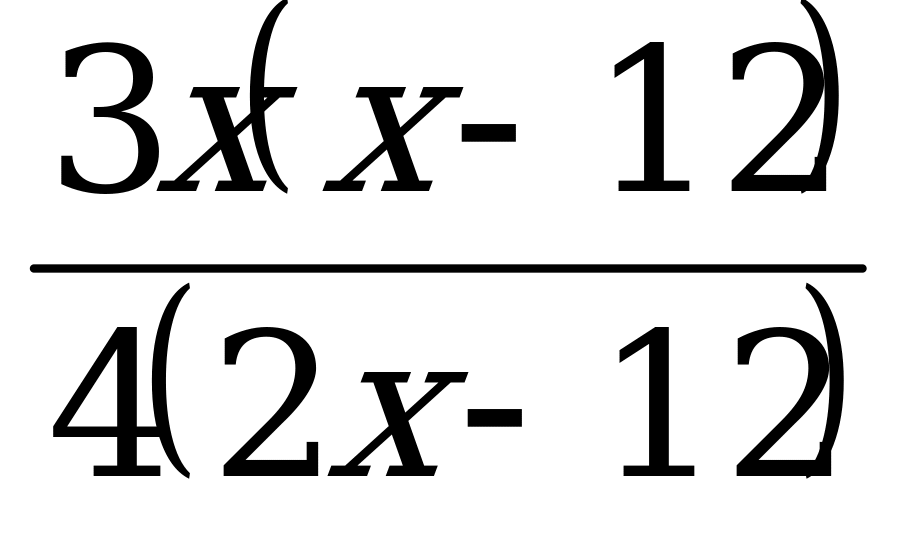 ч. Отсюда получаем уравнение:
ч. Отсюда получаем уравнение: 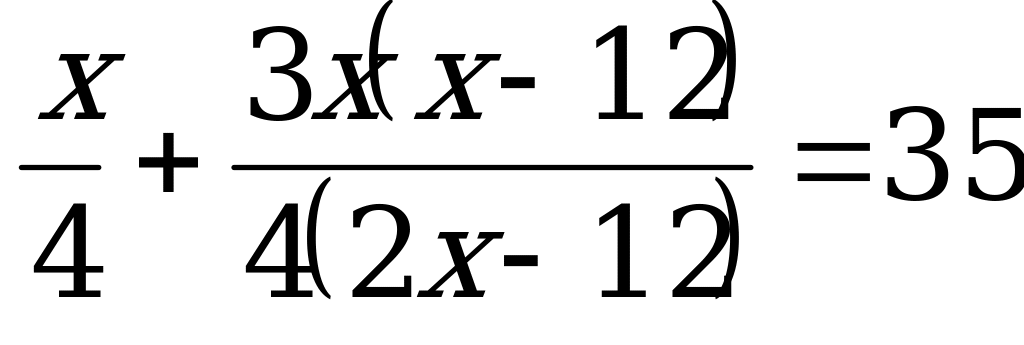
Решив это уравнение, найдем, что оно имеет два корня: 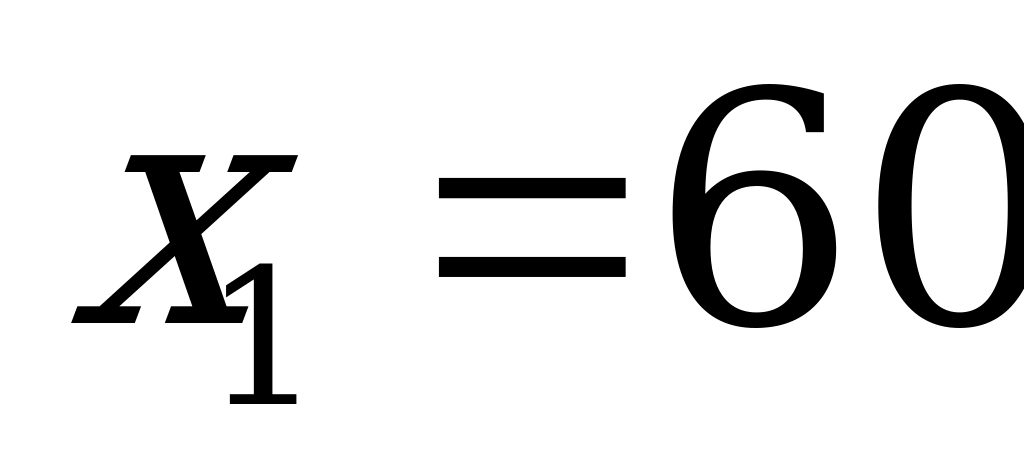 и
и 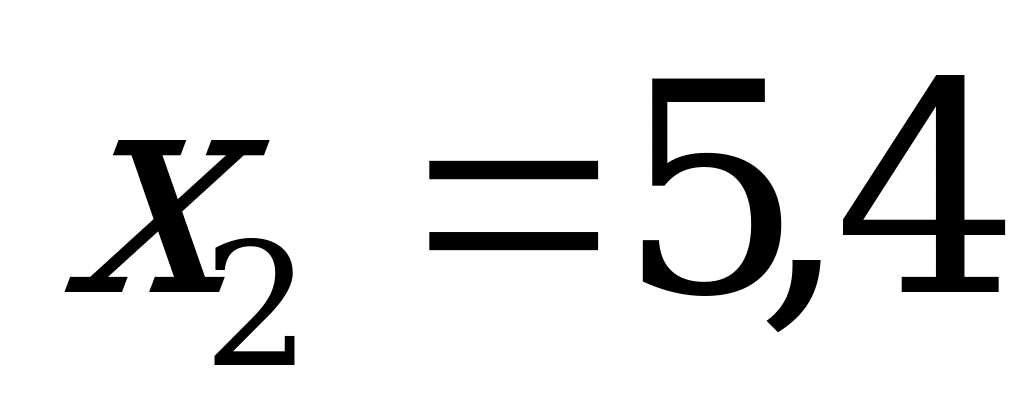 .
.
Второй корень не соответствует условию задачи.
Ответ: первой машинистке на перепечатку рукописи требуется 60 ч, а второй – 48 ч.
Задача 3. (содержание влаги).
Арбуз весил 20 кг и содержал 99 % воды, когда он немного усох, то стал содержать 98 % воды. Сколько теперь весит арбуз?
Решение:
Вес «сухого вещества» в арбузе составляет 100 - 99 = 1 (%) или 0,01, т. е. 200,01 =0,2 (кг).
25
После «усыхания» арбуза вес «сухого вещества» составляет 100 - 98 = 2 (%) или 0,2 : 0,02 = 10 (кг).
Ответ: 10 кг.
Задача 4. В референдуме приняли участие 60 % всех жителей одного из регионов города 14, имеющих право голоса. Сколько человек приняли участие в референдуме, если в районе около 180 тыс. жителей, а право голоса имеют 81 %?
Решение:
Найдем, сколько человек имеют право голоса
180-0,81 = 145,8 (тыс. чел.) Из них 60 % приняли участие в референдуме, т. е.
145,8-0,6 = 87,48 (тыс. чел.).
Ответ: 87 480 человек.
Задача 5. Из жителей города одни говорят только на украинском, другие – только на русском, третьи – на обоих языках. По-украински говорят 85% всех жителей, а по-русски – 75%. Сколько процентов всех жителей этого города говорят на обоих языках?
Решение:
100%-85%=15% - не говорят на украинском;
100%-75%=25% - не говорят на русском;
100%-15%-25%=60% - говорят на обоих языках.
Ответ: 60%
Самостоятельно с комментариями с места решить задачу № 128 .( Прилож. 2 )
III. Итоги занятия.
Домашнее задание. № 117, 120, 127.
Занятие 8.
Тема урока: "Задачи на проценты".
Тип урока: решение задач
Основные цели: тренировать способность к решению простых и составных в 2-3 действия на проценты; повторить и закрепить решение уравнений, упрощение выражений, запись выражений в виде дроби и их сокращение.
Ход занятия
I . Актуализация знаний и фиксация затруднения в деятельности.
а) 1) Находим какую часть 16 с составляет от 50 с: 16 : 50 = 0,32;
2) Выражаем, получившееся число в процентах: 0,32•100 = 32 (%)
3) Находим какую часть 2а составляет от 8а: 2а : 8а = 0,25
4) Выражаем, получившееся число в процентах: 0,25•100 = 25 (%).
1. Найдите x, если:
9% от x равно 8,1; (8,1 : 0,09 = 810 : 9 = 90)
7% от x равно 4,2; (4,2 : 0,07 = 420 : 7 = 60)
4% от xравно 1,2. (1,2 : 0,04 = 120 : 4 = 30)
П. Решение задач.
Задача 1. Имеются два сплава, состоящих из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй – 26% меди. Процентное содержание цинка в первом
и втором сплавах одинаково. Сплавив 150г первого сплава и 250г второго, получим новый сплав, в котором будет 30% цинка. Определить, сколько килограммов олова содержится в новом сплаве.
Решение:
Обозначим через х кг количество олова, содержащегося в получившемся новом сплаве, а через у кг – количество цинка, содержащегося в первом сплаве. Так как получившийся новый сплав весит 400 кг и в нем 30% цинка, то он содержит цинка
(400/100) 30 = 120кг, а тогда во втором сплаве цинка (120 – у) кг. По условию задачи процентное содержание цинка в первом и втором сплавах одинаково, поэтому имеем:
(y/150)∙100=((120-y)/250)∙100
Из этого уравнения находим, что у = 45. Поскольку первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет (40/100) ∙ 150 = 60 кг, а во втором сплаве олова будет (х – 60) кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет (250/100) ∙26 = 65 кг. Во втором сплаве олова содержится (х – 60) кг, цинка 120 – 45 = 75 кг, меди 65 кг и, так как все это весит 250 кг, то имеем х – 60 + 75 + 65 = 250,
откуда х = 170.
О т в е т: 170 кг.
Задача 2. Положив в банк деньги, вкладчик получил через год прибыль в 240 тысяч рублей. Однако он не стал забирать деньги из банка, а, добавив к ним еще 60 тысяч, снова оставил деньги на год. В результате спустя еще год он получил в банке 1 миллион 100 тысяч рублей. Какая сумма была положена в банк первоначально и какой процент прибыли в год давал банк?
Решение:
Допустим, что первоначальный вклад составляет 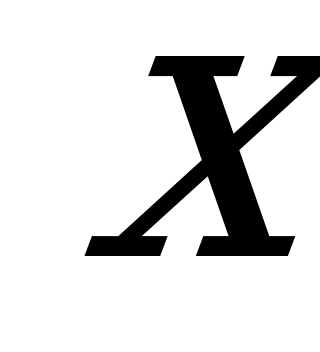 тысяч рублей. Тогда процент прибыли за год равен
тысяч рублей. Тогда процент прибыли за год равен 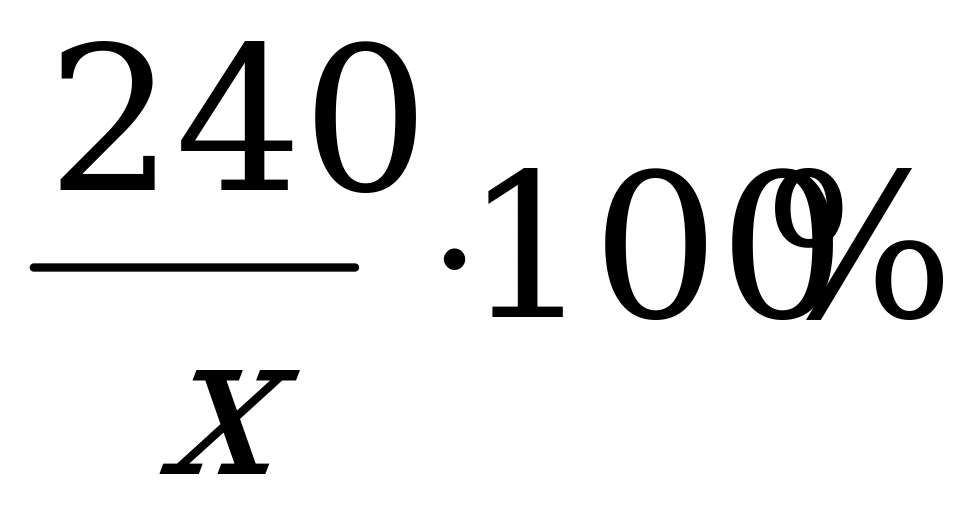 . Сумма вклада, положенного в банк через год, составила
. Сумма вклада, положенного в банк через год, составила 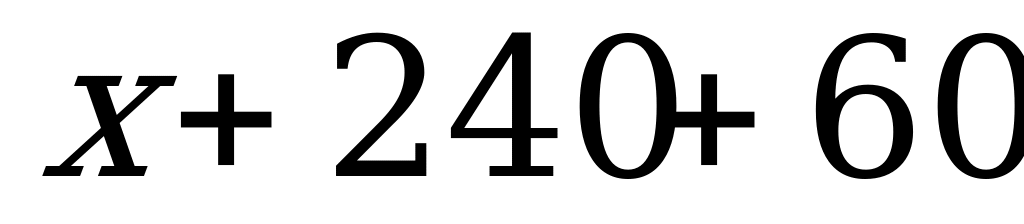 тысяч рублей, т.е.
тысяч рублей, т.е. 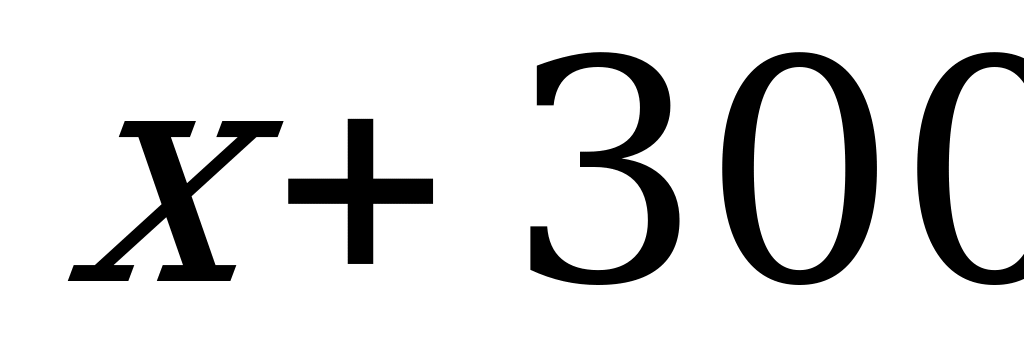 тысяч рублей. Этот вклад принес доход, равный
тысяч рублей. Этот вклад принес доход, равный 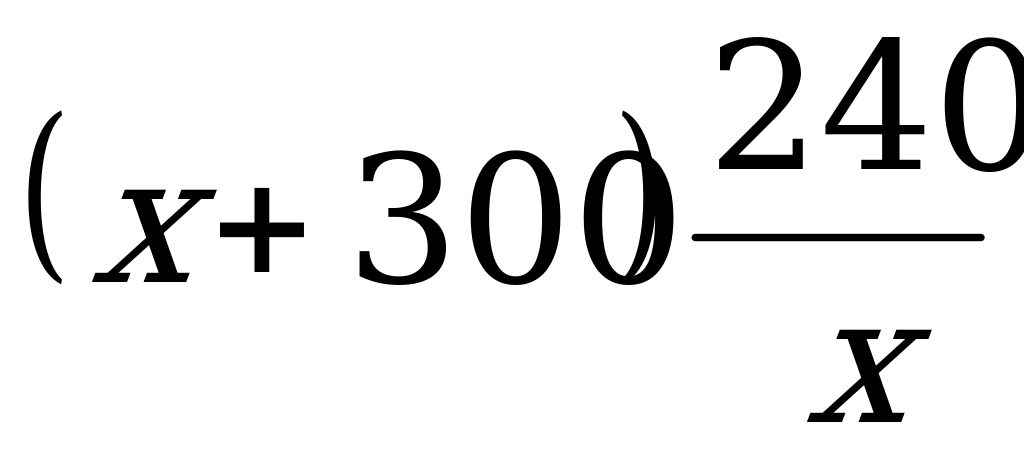 тысячам рублей. Всего вкладчик получил 1100 тысяч рублей.
тысячам рублей. Всего вкладчик получил 1100 тысяч рублей.
Получаем уравнение: 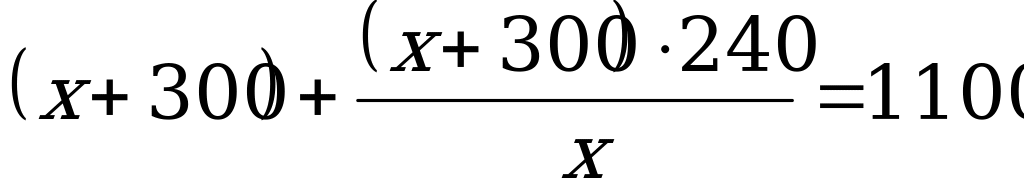
Решив его, найдем, что это уравнение имеет два корня: 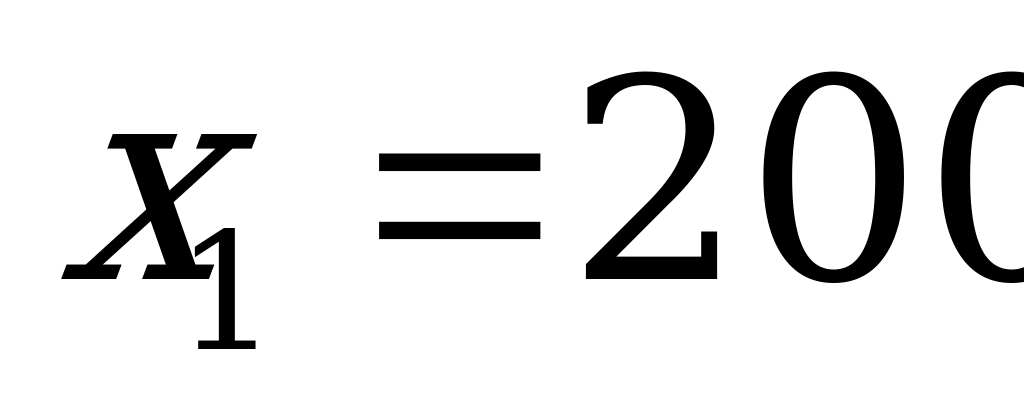 ,
, 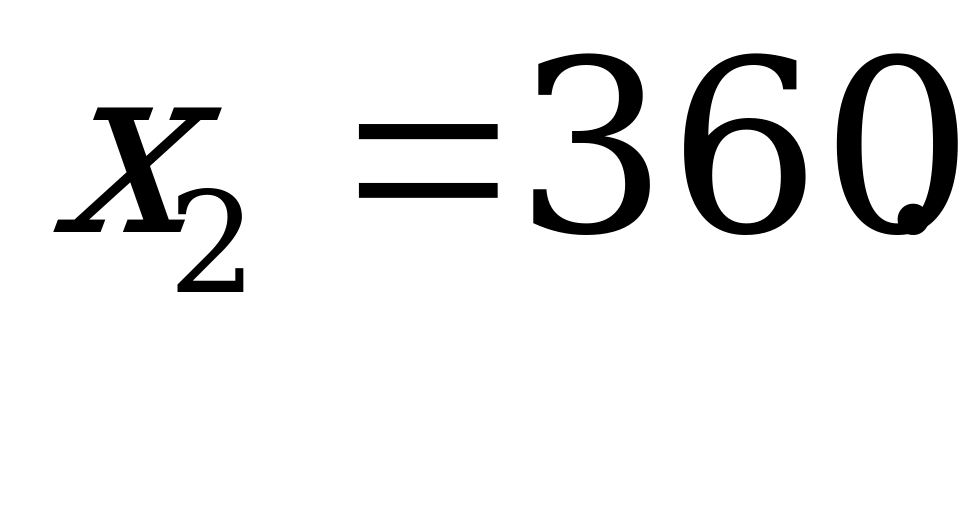 Выполнив расчеты, можно убедиться, что оба корня соответствует условию задачи.
Выполнив расчеты, можно убедиться, что оба корня соответствует условию задачи.
Ответ: задача имеет два решения: вкладчик вложил первоначально 200 тысяч рублей и получил доход 120% в год или вкладчик вложил первоначально 360 тысяч рублей и получил доход 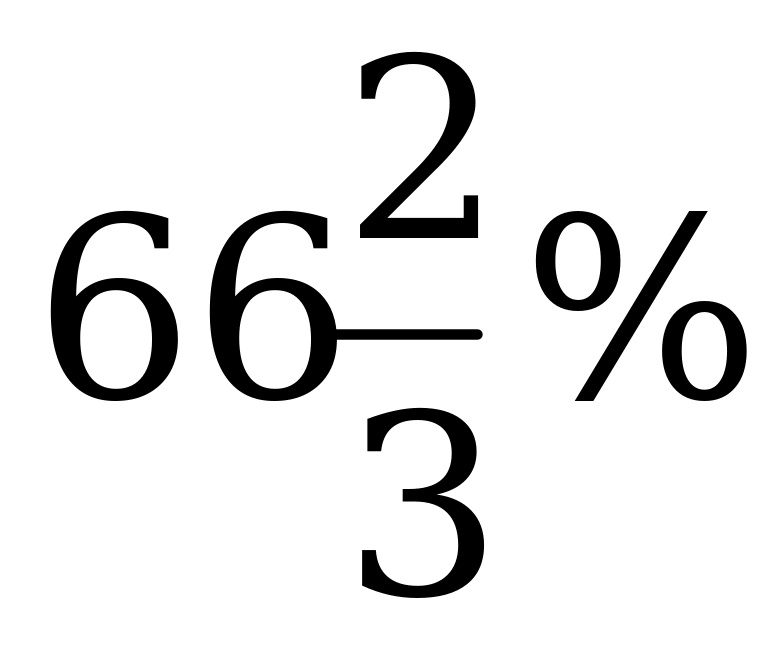 в год.
в год.
Задача 3. Имелось два слитка меди. Процент содержания меди в первом слитке был на 40 меньше, чем процент содержания меди во втором. После того как оба слитка сплавили, получили слиток, содержащий 36% меди. Найдите процентное содержание меди в первом и во втором слитках, если в первом слитке было 6 кг меди, а во втором – 12 кг.
Решение:
Обозначим за 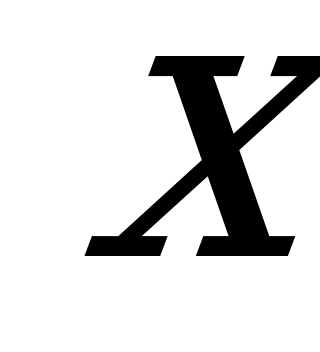 массу первого слитка в кг, за
массу первого слитка в кг, за 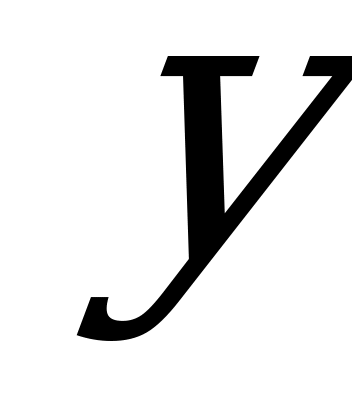 массу второго слитка в кг, получим систему уравнений:
массу второго слитка в кг, получим систему уравнений:
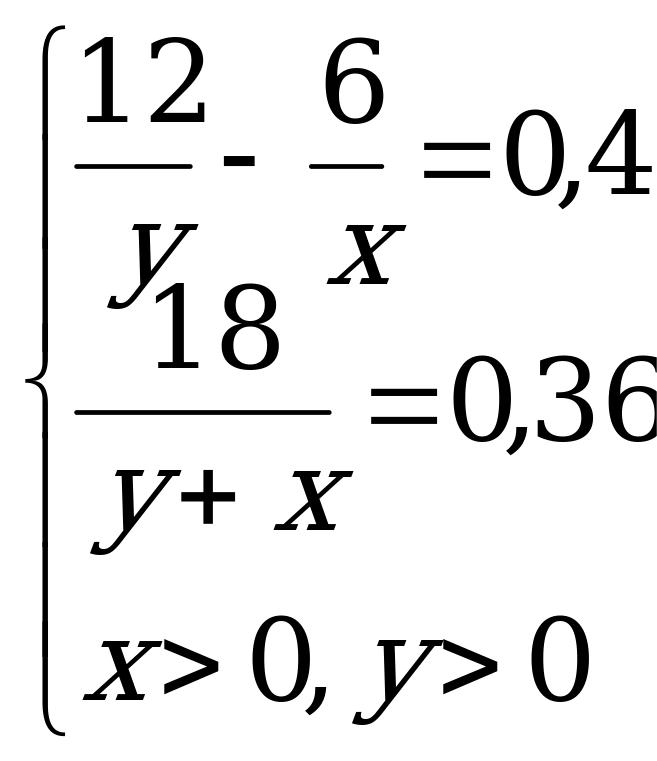
В результате получим: х=30, у=20.
Ответ: 30 кг, 20 кг
Задача 4. Для определения оптимального режима снижения цен социологи предложили фирме с 1 января снижать цену на один и тот же товар в двух магазинах двумя способами. В одном магазине – в начале каждого месяца (начиная с февраля) на 10%, в другом – через каждые два месяца, в начале третьего (начиная с марта) на одно и то же число процентов, причем такое, чтобы через полгода (1 июля) цены снова стали одинаковыми. На сколько процентов надо снижать цену товара через каждые два месяца во втором магазине?
Решение:
Пусть  руб. - стоимость товара,
руб. - стоимость товара,  - число процентов. Тогда,
- число процентов. Тогда,
I магазин
Февраль 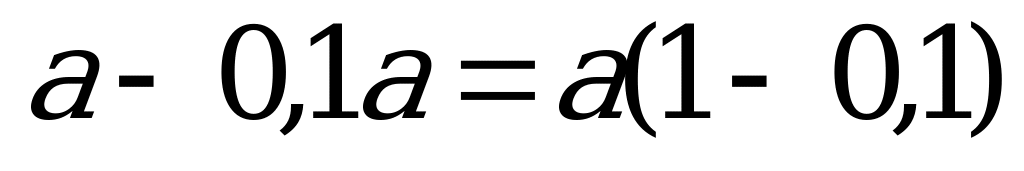
Март 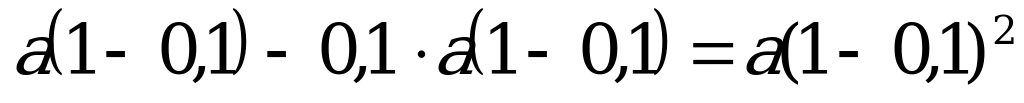
……………………………………
Июль 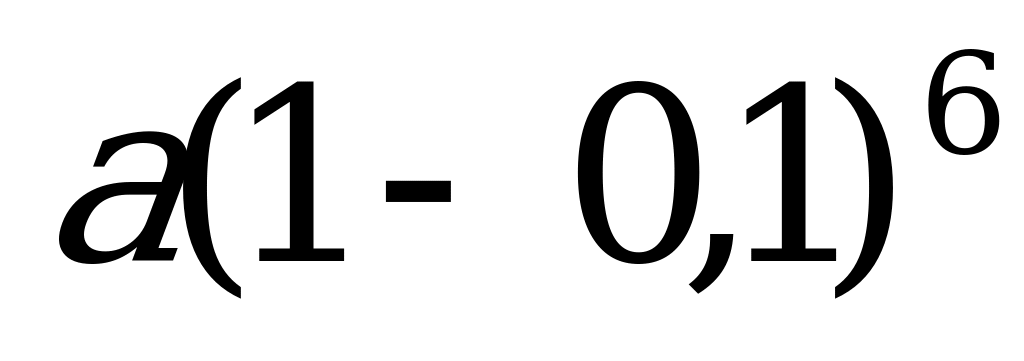
II магазин
Март 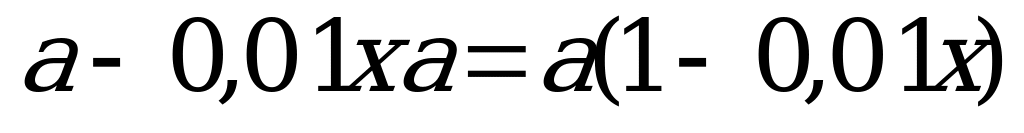
Май 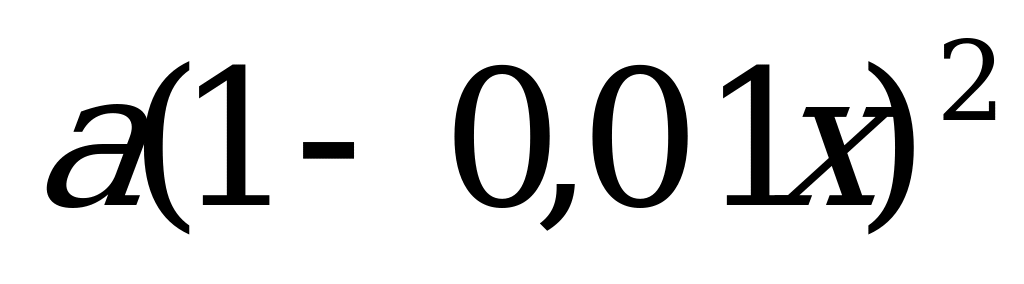
Июль 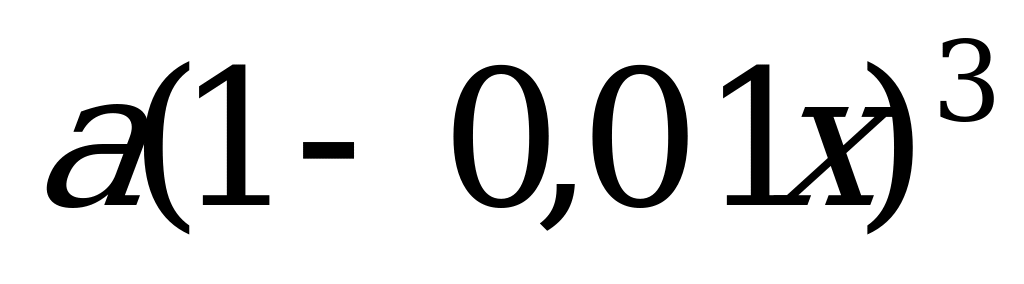
По условию задачи через полгода (1 июля) цены снова стали одинаковые, составляем уравнение:
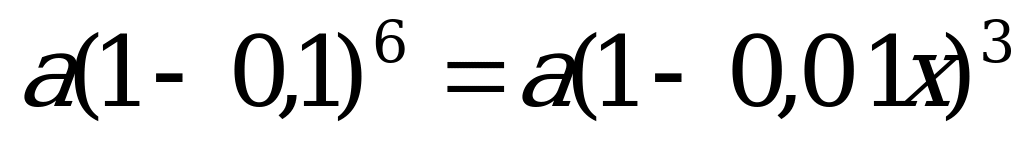
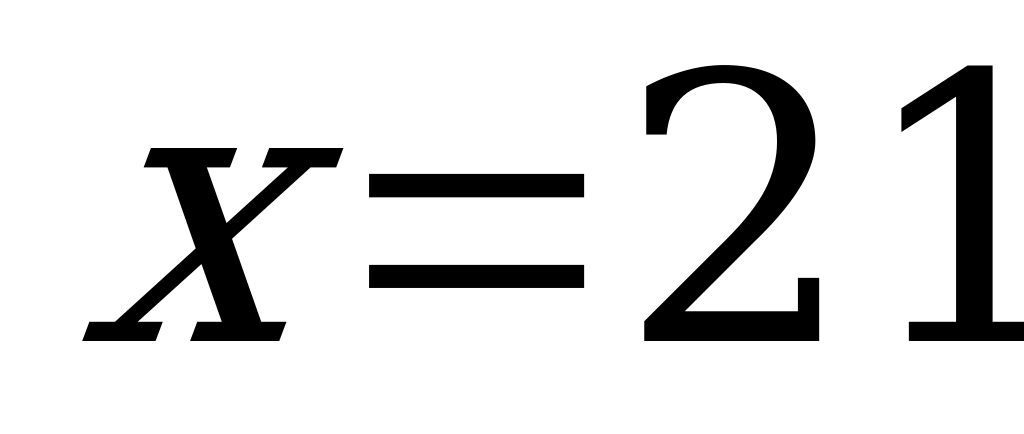
Ответ: на 21%.
Задачи для самостоятельной работы:
1. В соответствии с договором фирма с целью компенсации потерь от инфляции была обязана в начале каждого квартала повышать сотруднику зарплату на 3%. Однако в связи с финансовыми затруднениями она смогла повышать ему зарплату только раз в полгода (в начале следующего полугодия). На сколько процентов фирма должна повышать зарплату каждые полгода, чтобы 1 января следующего года зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренной договором.
Решение:
Пусть  руб. - зарплата,
руб. - зарплата, 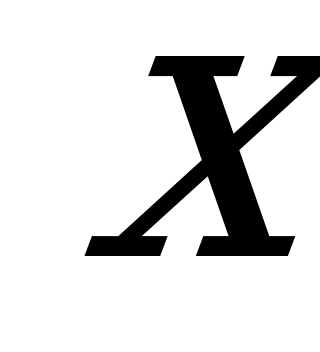 - процент повышения зарплаты. Тогда,
- процент повышения зарплаты. Тогда,
По плану
I квартал 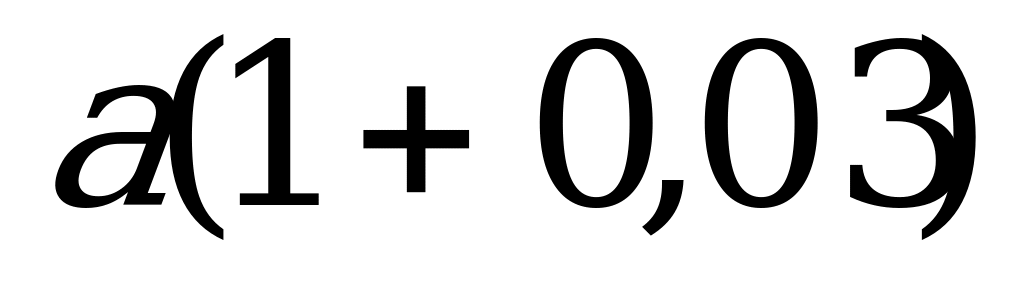 руб.
руб.
……………………………
IV квартал 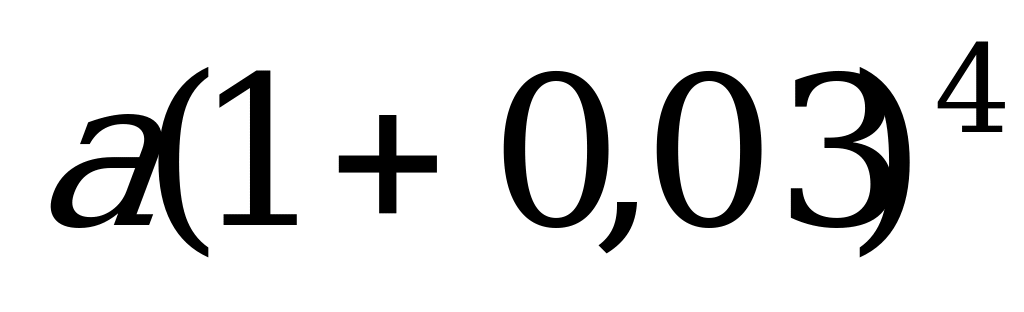 руб.
руб.
Фактически
I полугодие  руб.
руб.
II полугодие  руб.
руб.
По условию задачи зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренного договором, составляем уравнение:
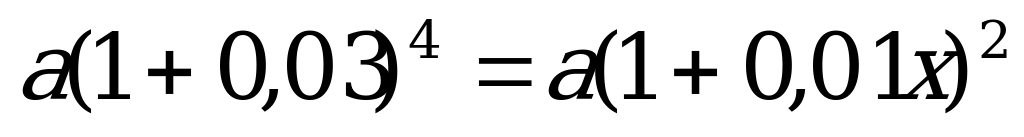
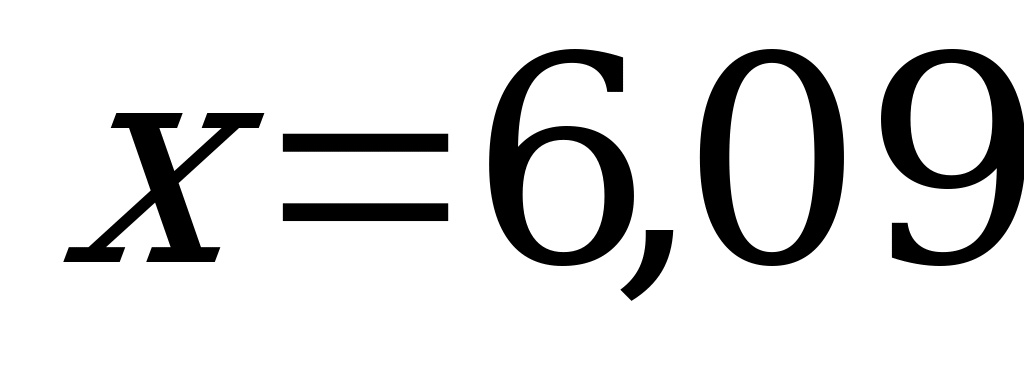
Ответ: на 6,09 %.
2. На заводе было введено рационализаторское предложение. В результате время, необходимое для изготовления рабочими некоторой детали, уменьшилось на 20%. На сколько процентов возросла производительность труда этого рабочего?
Решение:
Пусть 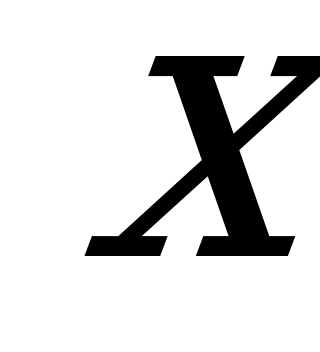 - производительность труда, а
- производительность труда, а  - весь объем работы. Тогда работа будет выполнена за время
- весь объем работы. Тогда работа будет выполнена за время  . В результате роста производительности труда время на изготовление детали стало равно
. В результате роста производительности труда время на изготовление детали стало равно 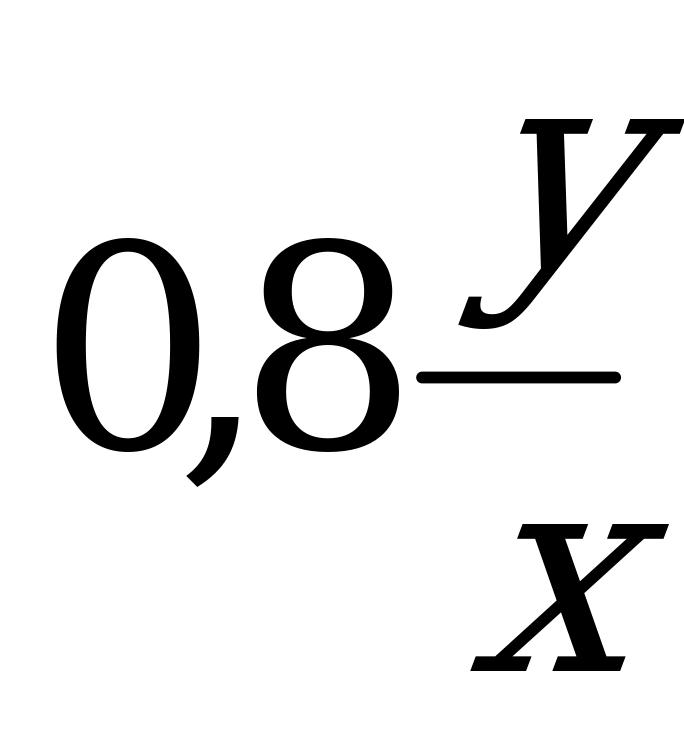 , соответственно производительность
, соответственно производительность 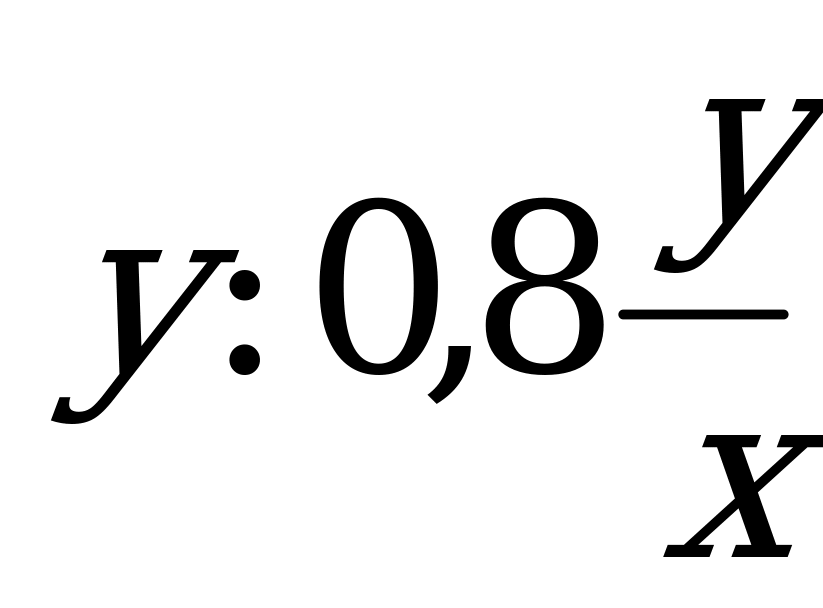 , или
, или 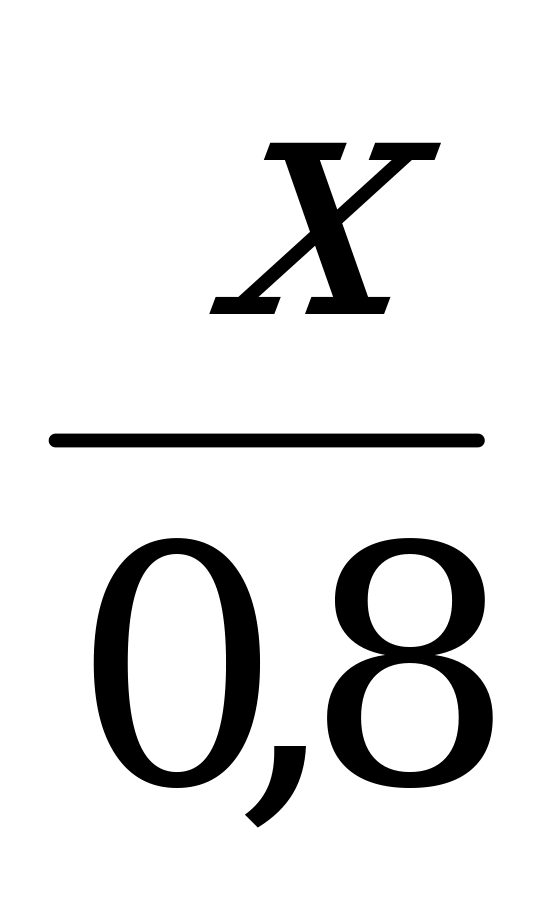 . Соответственно рост производительности труда составил:
. Соответственно рост производительности труда составил: 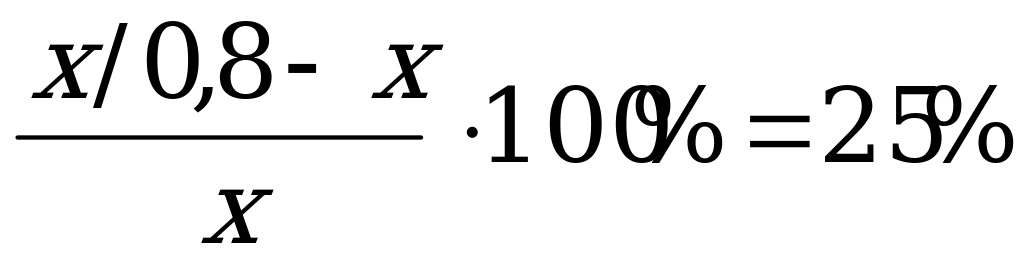
Ответ: 25%
Домашнее задание. ЗАДАЧИ ИЗ ЭКЗАМЕНАЦИОННОГО СБОРНИКА
(Приложение № 3)
Занятие 9.
Проверочная работа ( 1 ч )
Цель : выявление знаний учащихся и степени усвоения ими материала курса.
Ход занятия
I. Организация учащихся на выполнение работы.
П. Выполнение работы
Приложение № 5
Вариант 1
1. Квартирная плата повысилась на 20%. За прошлый месяц заплачено 120рублей. Сколько надо заплатить за текущий месяц?
2. В референдуме приняли участие 18 тыс. человек, что составило 60% всех жителей города, имеющих право голоса. Сколько жителей имеют право голоса?
3. В 5 тысячах из выпущенных 20 тысяч коробочек с жевательной резинкой находится сюрприз. Сколько процентов составили коробочки с сюрпризами?
4. Банком установлен тариф на пролонгацию аккредитива в размере 0,2% за квартал от суммы аккредитива. Вычислите размер комиссионных за пролонгацию аккредитива на сумму 100000 рублей за один квартал?
5. В первом квартале литр молока стоил 10 рублей. Во втором квартале цена на молоко повысилась на 20%, а в третьем еще на 50%. Сколько стал стоить литр молока?
6. Фирма платит разносчикам рекламных изданий за первую партию 10 тыс. рублей, а за каждую следующую в тот же день – на 5% больше по сравнению с предыдущей. Сколько получит человек, если в течение одного дня он разнес 4 партии изданий?
Вариант 2
1. 15% жителей города ежегодно слушают ВВС, 45% - радио «Свобода» и 40% - «Голос Америки». Можно ли сказать, что все жители города ежедневно слушают передачи западного радио?
2. Себестоимость товара 30 тыс. рублей. В магазине этот товар продается по цене 90 тыс. руб. Сколько процентов от себестоимости составляет розничная цена.
3. Валовой национальный продукт государства составил 33 млрд. долларов, что соответствует 75% от планировавшегося бюджетом. Найдите плановую величину НВП этого государства.
4. Подоходный налог установлен в размере 13%. До вычета подоходного налога 1% заработной платы отчисляется в пенсионный фонд. Работнику начислено 5420 рублей. Сколько он получит после указанных вычетов?
5. Инфляция составляет 10% каждый месяц. Сколько процентов составила инфляция за два месяца?
6. В результате мелиоративных мероприятий посевные площади увеличились на 150% по сравнению с прошлым годом. Найдите величину посевных площадей этого года, если в прошлом году она была 60 га.
III. Проверка работы. Анализ ошибок.
IV. Итоги занятия.

 Получите свидетельство
Получите свидетельство Вход
Вход


 5
5 0
0
 0
0  10 3
10 3
 х + у = 1,
х + у = 1,















 Проценты в нашей жизни (577.56 KB)
Проценты в нашей жизни (577.56 KB)
 0
0 86
86 0
0 Нравится
0
Нравится
0







