Производная функции

Урок обобщающего повторения по теме "Производная степенной функции." (2 курс)

Червакова Ирина Валериевна, преподаватель математики высшей квалификационной категории

Цели урока:

1. Познакомить с правилами дифференцирования на основе определения нахождения производных некоторых элементарных функций.

2. Формировать умения применять полученные знания по математике на уроках физики, биологии и химии, т.е. формирование целостного мировосприятия.

3. Отработать у учащихся приемы учебно-познавательной деятельности.

4. Активизировать личностный смысл учащихся к изучении темы.

5. Отработать у учащихся приемы учебно-познавательной деятельности.

Задачи урока:

1. Развивающая:

Учить логически мыслить, оценивать свои знания.

Совершенствовать умения самостоятельного поиска информации, умения анализировать, систематизировать, выбирать главное, способствующие формирование информационной и учебно – познавательной компетенции школьников.

1. Учебная:

Организовать деятельность учащихся по обобщению и систематизации знаний нахождения производных, отработать применение правил дифференцирования.

1. Воспитательная:

Развивать умения работать в группе, способствующие формированию коммуникативной компетенции школьников. Формировать эмоционально-ценностное отношение к учебной деятельности, воспитывать интерес к математике.

Используемые педагогические технологии, методы и приемы.

Здоровьесберегающая технология, проектная технология, ИКТ технология.

Время реализации мероприятия, занятия: 45 мин.

Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. студенты в ходе урока:

1. Систематизации знаний табличных производных. Нахождение новых производных

2. Формирование умений применять табличные производные;

3. умение извлекать необходимую информацию из различного рода источников;

4. навыки пользоваться правилами дифференцирования;

5. умение работать в команде.

Необходимое оборудование и материалы: Интердоска, портреты математиков, мультимедийная разработка урока, бланки листов для проведения программированного контроля

Список учебной и дополнительной литературы:

1. http://festival.1september.ru/

2. Колмогоров М.Н «Алгебра и начала анализа», Москва, «Просвещение»,2006 г.10-11 класс,

3. Фридман Л.М. «Учитесь учиться математике», Москва, «Просвещение», 1995 г.

4. Журнал «Математика»

5. Газета «Математика в школе». Приложение к журналу «Первое сентября»

6. Материалы ЕГЭ

7. Башмаков М.И. учебник математика (для НПО и СПО).

10—11 кл. – М., 2012.

1. Башмаков М.И. Математика (для НПО и СПО). Сборник задач:

учеб.пособие. – М., 20012.

1. do.rksi.runhtk-edu.ru

2. festival.1september.ru

3. e-mediatech.com

4. edu.ru

5. http://yotx.ru/default.aspx

6. http://matesha.ru/

Ход урока

1) Тема нашего урока «Производная степенной функции». Откроем тетради, запишем число и тему урока.

На предыдущих уроках мы выводили табличные производные, доказывали правила дифференцирования и учились практическому применению. Сегодня мы должны повторить производные, правила дифференцирования, закрепить навык их нахождения, дополнить таблицу производных.

2) Повторим таблицу производных, и правила вычисления производных (слайд 5,6)

3) Задание №1:Найди соответствие (устно): (слайд 7,8) (количество правильных совпавших ответов = количеству баллов за это задание, максимум 10 балов)(3-4мин)

4) Задание №2: Найди производные функций (устно). (Слайд 9) (правильный ответ1 балла)(2 мин)

5) Задание №3: Найди ошибку: (слайд 10) (правильный ответ 2 балла) (2 мин)

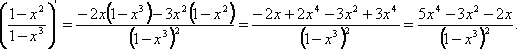
6) Задание №4: «Смотри не ошибись!»: (задания на доске, учащиеся по очереди выходят и решают примеры). (10 мин)

1) (4х²+…..)= (……)΄+ (х²)ʹ=….. (1 балл)

2) (…..-2√х)΄=(1/х)΄- (…..)ʹ=……(1балл)

3) ((3х-1)/(….))=((…..)ʹ(……) -(…..)(х³)ʹ)/(х³)²=^……..(2 балл)

4) (3х²*(…..))΄= (…)ʹ*√х+ (….)(….)ʹ=…..(2 балл)

5) ((1/2х-4)⁸)ʹ=… (3 балл)

7) ) Задание №5: «Кто быстрее?»: Найти значение производной в точке х₀=0 (к доске выходят двое учащихся и решают пример на скорость, остальные работают в тетради): (6 мин)

1) у= (7х+4)/(1-3х) (3 балл) 2) у= (2х-1)/(3-5х) (3 балл)

Ответ: у(0)=19 ответ: у(0)= 1/9

8) ) Задание №6: При каком значении х производная функции =4?(работа в тетради, один учащийся у доски)(4 мин)

У= 1/3х³+х²+х Ответ: х=1 и х=-3. (3 балл)

9) Подведение итогов за урок, выставление оценок. (3 мин) (Слайд 11) Учащиеся получают за урок баллы, которые в конце урока обмениваются на оценку:

10-11 баллов- 3(удовлетворительно)

12-14 баллов- 4 (хорошо)

15 баллов -5(отлично)

Учащиеся подсчитывают свои баллы, переводят их в оценку и сообщают преподавателю для выставления оценки в журнал.

10) Закончим мы с вами историей дифференциального исчисления, и познакомимся с учеными, которые внесли большой вклад в развитие дифференциального исчисления. (Слайд 12-25)(10 мин)

Как один из вариантов, можно предложить в конце урока решить кроссворд.

ГАПОУ КО ОКТУ