Цели.
Обучающая: повторить понятия четности, монотонности, экстремумов, применить их для заданий, в которых функция задана графиком или графиком ее производной.
Развивающая: развить способности мыслить в нестандартной ситуации.
Воспитательная: привить безбоязненное отношение к заданиям, часто встречающимся в ЕГЭ, в которых функция задана графиком.
Формы обучения: фронтальный опрос, выполнение заданий и рассмотрение их решения с помощью презентации через проектор, самостоятельная работа.
Методы обучения: продуктивный (обратная связь как показ усвоенных знаний), проблемный (при постановке проблемы и решении ее с помощью применения изученного материала в заданиях, сформулированных в нестандартной форме).
Оборудование: подготовленная презентация, проектор, экран, ноутбук, раздаточный материал: рисунки с графиками функций, производных, задание самостоятельной работы.
Ход урока
I. Организационный момент (домашнее задание, объявление целей и темы урока).
II. Выполнение заданий с помощью графиков функций (вопросы и задания появляются последовательно на экране в презентации; ответы комментируются учителем математики и записываются на доске учителем или вызванным учащимся; каждому учащемуся выдаются рисунки с графиками).
Вопросы:
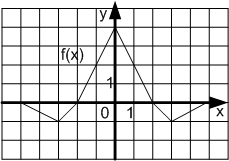
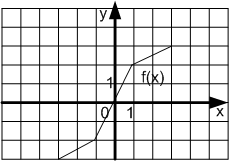
1. Какие функции называются четными?
2. Каким свойством обладают графики четных функций?
3. Какие функции называются нечетными?
4. Каким свойством обладают графики нечетных функций?
Задание 1. Определить по графику, какая из функций является четной, какая нечетной.
Вопросы:
5. Что называется нулями функции?
6. Как изображаются нули функции на графиках?
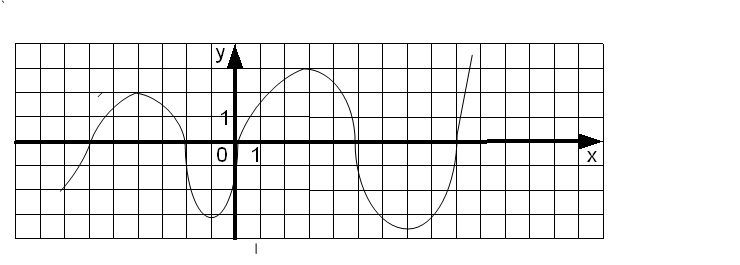
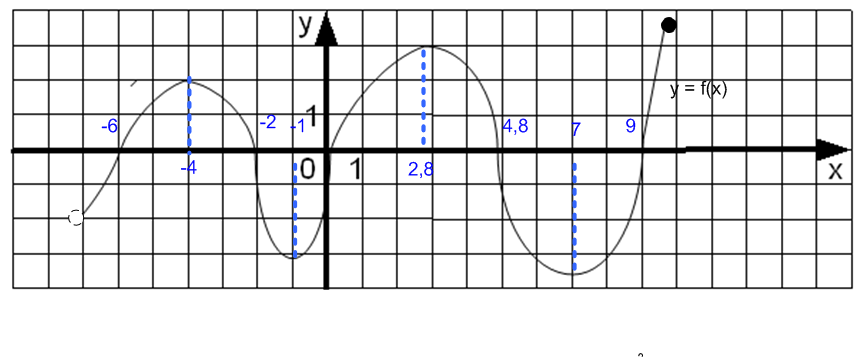
Задание 2. Определить количество нулей функции на (-7; 10] (график №3 из задания 1).
Во время выполнения задания последовательно на экране появляются точки – нули функции и ответ: 5.
Вопросы:
7. Какая функция называется возрастающей на промежутке?
8. Какая функция называется убывающей на промежутке?
Задание 3. Определить промежутки возрастания функции (график №3 из задания 1).
На экране последовательно появляются промежутки возрастания функции, ответ: (-7; -4] и на [-1; 2,8] и на [7; 10]. Акцентируется внимание учащихся на часто встречающиеся ошибки при записи ответов:
- не ставится знак объединения между промежутками;
- концы промежутков, в которых функция определена, включаются в ответ.
Задание 4. Определить промежутки убывания функции (график №3 из задания 1).
Самостоятельное решение задания с последующей проверкой.
Аналогично предыдущему заданию на экране должны появиться промежутки убывания функции и ответ: [-4; -1] и на [2,8; 7].
Задание 5. Определить количество корней уравнения f(x) = 1(график №3 из задания 1). Как графически найти корни данного уравнения?
В презентации организуется последовательное появление на экране прямой – графика функции y = 1, точек пересечения графиков функций y = 1 и y = f(x), абсцисс этих точек пересечения и ответа: 5. Заостряется внимание на то, что при графическом решении уравнения ответом являются абсциссы точек пересечения графиков функций.
Задание 6. Решить неравенство f(x) ≤ 1(график №3 из задания 1).
Вопрос. Что значит графически решить неравенство?
Ответ. Построить графики функций, определить промежутки, для которых точки графика функции f(x) расположены ниже точек графика функции y = 1, и абсциссы точек пересечения графиков, т.к. неравенство нестрогое.
На экране последовательно появляются: прямая – график функции y = 1, абсциссы точек пересечения графиков функций y = 1 и y = f(x), промежутки, которые являются решением неравенства, ответ: (-7; -5,4] V [-2,6; 0,5] V [4,7; 9,2]. Проверяется умение правильно записывать промежутки при решении неравенств.
Вопрос. Почему х = -7 исключено из решения неравенства?
Ответ. Т.к. при этом значении аргумента функция не определена.
Вопрос. Почему остальные концы промежутков в ответ включены?
Ответ. Т.к. неравенство нестрогое.
Вопрос. Можно ли при записи ответа пользоваться значком объединения?
Ответ. Да.
Задание 7. Решить неравенство f(x) > 1(график №3 из задания 1).
Самостоятельное решение задания с последующей проверкой.
Аналогично предыдущему заданию на экране последовательно появляются: прямая – график функции y = 1, абсциссы точек пересечения графиков функций y = 1 и y = f(x), промежутки – решение неравенства, ответ: (-5,4; -2,6) V (0,5; 4,7) V (9,2; 10]. Обратить внимание на правильную запись ответа.
Задание 8. Решить неравенство f(x) > 0 (график №3 из задания 1).
Самостоятельное решение задания с последующей проверкой.
Во время выполнения задания на экране последовательно появляются промежутки значений x, при которых точки графика функции y = f(x) находятся выше оси абсцисс, и ответ: (-6; -2) V (0; 4,8) V (9; 10].
Вопрос. Почему х = 10 является решением неравенства?
Ответ. Т.к. при х = -6; -2; 0; 4,8; 9 значения функции равны нулю, а при х = 10 f(x) > 0.
Задание 9. Решить неравенство f(x) ≤ 0 (график №3 из задания 1).
Самостоятельное решение задания с последующей проверкой.
Аналогично предыдущему заданию последовательно на экране появляются промежутки значений x, при которых точки графика функции y = f(x) находятся ниже оси абсцисс или лежат на ней, и ответ: (-7; -6] V [-2; 0] V [4,8; 9].
Задание 10. На рисунке изображены графики функций y = f(x) и y = g(x), заданных на промежутке [-8; 11]. Укажите множество всех значений x, для которых выполняются неравенства: a) f(x) ≥ g(x); б) f(x) < g(x).
Вопрос. Как вы думаете, на что нужно обратить внимание при решении подобных заданий?
Ответ. 1) Найти абсциссы точек пересечения графиков функций.
2) Выяснить, при каких значениях аргумента точки графика одной функции расположены выше (ниже) точек графика другой функции.
Для проверки ответа на рисунке последовательно появляются промежуток значений x, при котором точки графика функции y = f(x) находятся выше точек графика функции y = g(x) или совпадают, и ответ: [-6; 6]. Затем, после исчезновения предыдущего промежутка, появляются промежуток значений x, при котором точки графика функции y = f(x) находятся ниже точек графика функции y = g(x), и ответ: [-8; -6) V (6; 11].
III. Выполнение заданий с помощью графика производной функции.
Перед следующим заданием идет проверка на доске одного номера из домашнего задания на исследование функции y = x6 ∙ e–x на экстремумы аналитическим способом, чтобы напомнить учащимся план такого исследования: нахождение области определения функции, нахождение производной, критических точек, определение промежутков возрастания и убывания функции, точек экстремума. Одновременно строится схема, отображающая все пункты плана исследования функции.
D(f) = R;
y′ = x 5 ∙ e–x ∙(6 - x);
y′ = 0 при x = 0, x = 6;
определить знаки производной в каждом промежутке;
функция убывает на (-∞; 0] и на [6; ∞)
функция возрастает на [0; 6];
x = 0 –точка минимума
x = 6 – точка максимума.
Этот план исследования функции на экстремумы аналитическим способом и подобная схема в следующем задании используется для исследования функции, заданной графиком ее производной.
Задание 11. По графику производной некоторой функции определить (задания и ответы на них появляются на экране; каждый учащийся строит схему в тетради):
- область определения функции (D(f) = [-8; 14]);
- критические точки (x = -7, -3, 5, 9, 13);
- промежутки возрастания функции ( [-7; -3] и на [5; 9] и на [13; 14] ) и промежутки убывания функции ( (-8; -7] и на [-3; 5] и на [9; 13] );
- точки экстремума (x = -7, 5, 13 – точки минимума, x = -3, 9 – точки максимума).
После построения схемы по графику производной можно ответить на многие вопросы: определить промежутки монотонности функции, количество точек экстремума, характер точек экстремума.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



 3)
3)














 Исследование функций на четность, монотонность, точки экстремума (0.42 MB)
Исследование функций на четность, монотонность, точки экстремума (0.42 MB)
 1
1 984
984 135
135 Нравится
0
Нравится
0


