Презентация к уроку законы логики

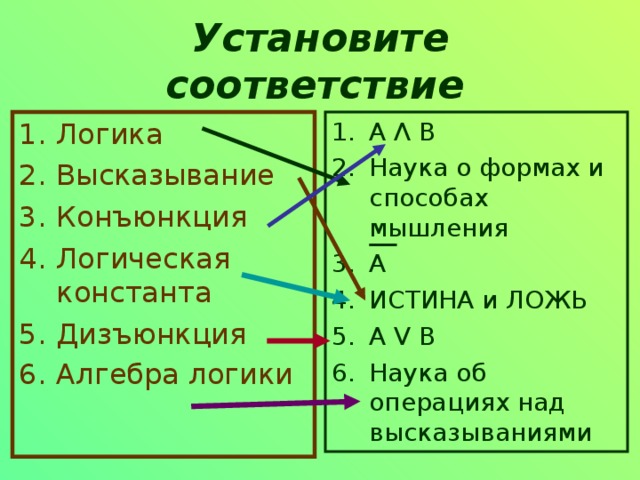
Установите соответствие

• Логика
• Высказывание
• Конъюнкция
• Логическая константа
• Дизъюнкция
• Алгебра логики

• А Λ В
• Наука о формах и способах мышления
• А
• ИСТИНА и ЛОЖЬ
• А V В
• Наука об операциях над высказываниями

Растение, знающее практически каждого.

Хрен

Под каким деревом сидит заяц, когда идет дождь?

Под мокрым

Когда человек бывает в комнате без головы?

Когда высовывает ее из окна на улицу

Сколько месяцев в году имеют 28 дней?

Все месяцы

Переместительный

Дизъюнкция:

X  Y ≡ Y  X

Конъюнкция:

X  Y ≡ Y  X

Основные законы алгебры высказываний

Сочетательный

Дизъюнкция:

X  (Y  Z) ≡ (X  Y)  Z

Конъюнкция:

X  (Y  Z) ≡ (X  Y)  Z

Распределительный

Дизъюнкция:

X  (Y  Z) ≡ X  Y  X  Z

Конъюнкция:

X  (Y  Z) ≡ (X  Y)  (X  Z)

Основные законы алгебры высказываний

Правила де Моргана

Дизъюнкция:

¬ (X  Y) ≡ ¬ X  ¬ Y

Конъюнкция:

¬ (X  Y) ≡ ¬X  ¬ Y

Основные законы алгебры высказываний

Идемпотенции

Дизъюнкция:

X  X ≡ X

Конъюнкция:

X  X ≡ X

Основные законы алгебры высказываний

Поглощения

Дизъюнкция:

X  (X  Y) ≡ X

Конъюнкция:

X  (X  Y) ≡ X

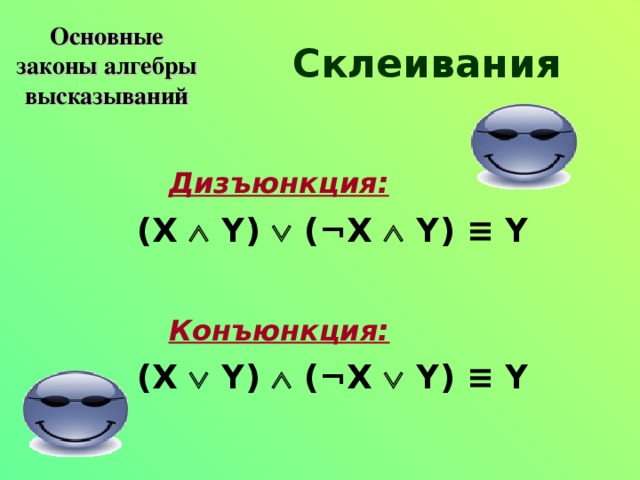
Основные законы алгебры высказываний

Склеивания

Дизъюнкция:

(X  Y)  ( ¬ X  Y) ≡ Y

Конъюнкция:

(X  Y)  ( ¬ X  Y) ≡ Y

Основные законы алгебры высказываний

Переменная со своей инверсией

Дизъюнкция:

X  ¬ X ≡ 1

Конъюнкция:

X  ¬ X ≡ 0

Основные законы алгебры высказываний

Операция с константами

Дизъюнкция:

X  0 ≡ X, X  1 ≡ 1

Конъюнкция:

X  0 ≡ 0, X  1 ≡ X

Основные законы алгебры высказываний

Двойного отрицания

¬(¬ X) ≡ X

Х = Х

Закон контрапозиции (правило перевертывания)

• (A Û  B) = (BÛ A)

┐ (А→В) = А&┐В

┐ А&(АÚВ)= ┐А&В

АÚ┐А&В=АÚВ

Порядок действий

• Действия в скобках
• Отрицание
• Конъюнкция
• Дизъюнкция
• Импликация
• Эквивалентность

Выполни гимнастику для глаз по схеме:

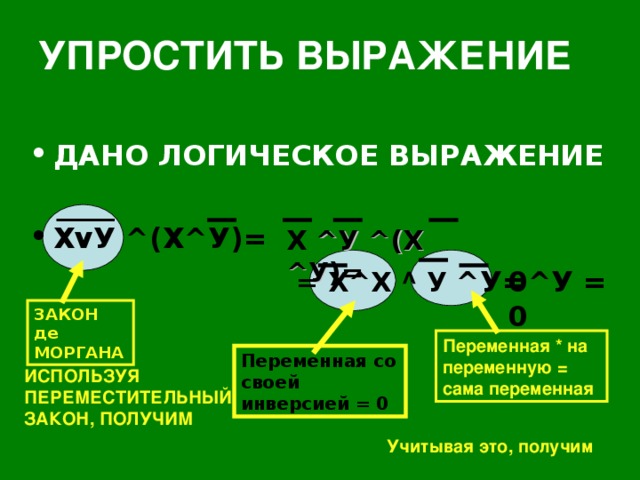
УПРОСТИТЬ ВЫРАЖЕНИЕ

• ДАНО ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ

• Х v У ^ (Х ^ У)=

Х ^ У ^ (Х ^ У)=

= Х ^ Х ^ У ^ У=

0 ^ У = 0

ЗАКОН де МОРГАНА

Переменная * на переменную = сама переменная

Переменная со своей инверсией = 0

ИСПОЛЬЗУЯ ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН, ПОЛУЧИМ

Учитывая это, получим

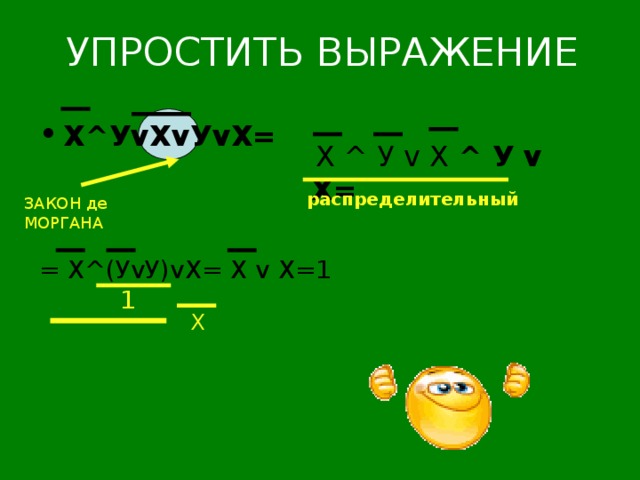
УПРОСТИТЬ ВЫРАЖЕНИЕ

• Х ^ У v Х v У v Х=

Х ^ У v Х ^ У v Х=

распределительный

ЗАКОН де МОРГАНА

= Х ^ (У v У) v Х=

Х v Х=1

1

Х

(B ∙A) " width="640"

УПРОСТИТЬ

1.   ¬ (А ∙В ∙С)+ ¬ ¬ ( А +В +¬С) 2.     ¬ (А + В) = (B ∙A)