Презентация по информатике "СКНФ или СДНФ. Получение схемы логического элемента по заданным значениям логической функции"

Презентация предназначена для поддержки углубленного изучения темы Логика на уроке Информатики и ИКТ в 10 классе и может применяться на заключительных уроках  темы.

В презентации подробно рассмотрено:

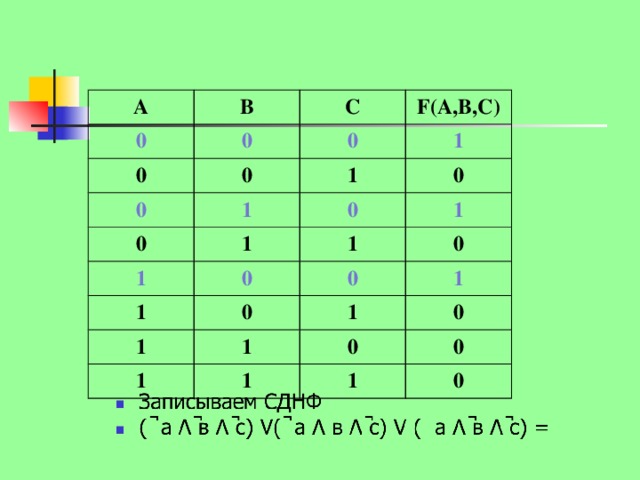
применение СКНФ или СДНФ для получения логического выражения по итоговым значениям логической функции от нескольких логических переменных; 

применение законов логики для упрощения логических функций от нескольких переменных по оптимальному алгоритму;

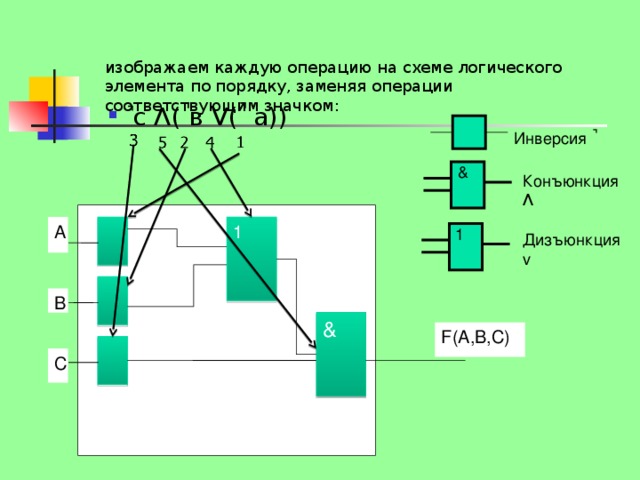
описан алгоритм построения схемы логического элемента по его формуле.

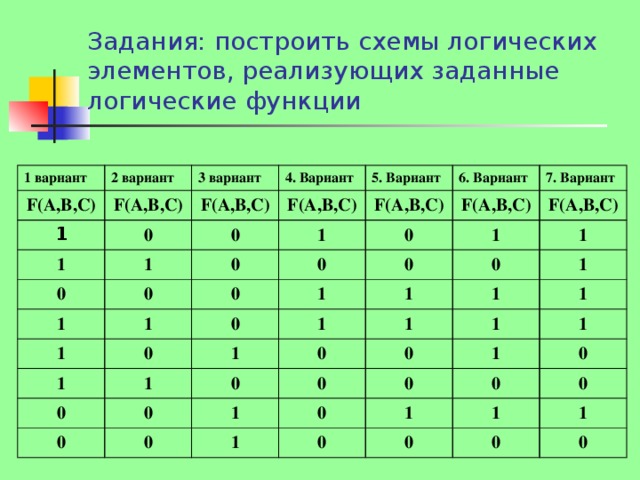
Презентация содержит 7 вариантов контрольных заданий и ключи к ним.

Домашнее задание творческое, связанное с анализом и упрощением схемы логического элемента.

Конъюнкция – логическое умножение.

Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые

Дизъюнкция –логическое сложение.

Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые

Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ).

Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной  нормальной формой. 

Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ

Учитель Информатики и ИКТ

Тропин Константин Львович

МБОУ Гимназия

г.Новый Уренгой

2014г.

Определения:

• Конъюнкция – логическое умножение.
• Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые: ¬C Λ C; C Λ ¬A; ¬C Λ B Λ ¬A ;
• Дизъюнкция –логическое сложение.
• Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые: ¬CVC; CV¬A; ¬CVBV¬A ;

ДНФ и КНФ

• Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ): (CΛCΛ¬B)V(¬CΛA)
• Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной  нормальной формой (КНФ): (CVCV¬ B)Λ(¬CVA)

СКНФ и СДНФ

• Cовершенной ДНФ называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз ( возможно с отрицанием) (C Λ B Λ ¬A)V (C Λ B Λ A)
•   Cовершенной КНФ называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз  ( возможно с отрицанием) (¬ CVBVA) Λ(C V¬BVA)

Алгоритм получения СДНФ по таблице истинности:

Дана таблица итоговых значений логической функции

• Записываем исходные значения логических переменных.
• Применяем СДНФ (так как значений «1» меньше):
• Обрабатываем те строки ТИ, в последнем столбце которых стоят «1»
• Выписываем для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение логической переменной в данной строке =1, то в конъюнкцию включают саму эту переменную, если =0, то ее отрицание:
• Все полученные конъюнкции связать в дизъюнкцией (записать произведение сумм):
• Упрощаем логическое выражение, применяя законы алгебры логики

• Склеивания Распределительный Поглощения
• Склеивания
• Распределительный
• Поглощения

F(А,В,С)

1

0

1

0

1

0

0

0

А

0

В

С

0

0

F(А,В,С)

0

0

0

1

1

1

0

1

0

0

1

0

1

1

1

0

0

1

0

1

1

1

1

0

0

1

0

1

0

• 1) Применяем закон склеивания к 1-му и 3-му выражениям ( ̚ а Λ ̚в Λ ̚с ) V( ̚ а Λ в Λ ̚с) V ( а Λ ̚в Λ ̚с ) =
• 2) Применяем распределительный закон ( ̚в Λ ̚с) V( ̚ а Λ в Λ ̚ с ) =
• 3) Применяем закон поглощения ̚с Λ ( ̚ в V( ̚ а Λ в ))= ̚с Λ( ̚в V( ̚ а))
• 4) Проставляем на полученной формуле порядок выполнения логических операций согласно приоритета.

• ̚ с Λ( ̚в V( ̚ а))

3

1

2

5

4

изображаем каждую операцию на схеме логического элемента по порядку, заменяя операции соответствующим значком:

• ̚ с Λ( ̚в V( ̚ а))

Инверсия ̚

&

Конъюнкция Λ

1

А

1

Дизъюнкция v

В

&

F(A,B,C)

С

Алгоритм получения СКНФ по таблице истинности:

(В случае если среди значений функции значений «0»меньше, применяют СКНФ)

• Отметить те строки таблицы истинности, в последнем столбце которых стоят 0:
• Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке =0, то в дизъюнкцию включают саму эту переменную, если =1, то ее отрицание:
• Все полученные дизъюнкции связать в конъюнкцию(записать сумму произведений):
• Упростить логическое выражение, применив законы

• Склеивания Распределительный Поглощения
• Склеивания
• Распределительный
• Поглощения
• (Предлагается выполнить самостоятельно)

Задания: построить схемы логических элементов, реализующих заданные логические функции

1 вариант

2 вариант

F(А,В,С)

1

3 вариант

F(А,В,С)

4. Вариант

0

1

F(А,В,С)

0

1

0

F(А,В,С)

5. Вариант

6. Вариант

0

1

1

0

F(А,В,С)

7. Вариант

F(А,В,С)

0

1

1

0

0

0

1

1

0

1

0

F(А,В,С)

1

1

0

1

0

1

1

0

0

1

0

1

1

0

1

0

1

0

1

0

1

0

0

1

1

0

0

0

1

1

0

0

1

0

0

Логические операции в порядке приоритета

Инверсия ̚

&

Конъюнкция Λ

1

Дизъюнкция v

Домашнее задание

• Анализ и упрощение логической схемы:

• Нарисовать схему логического элемента с тремя логическими входами (X,Y,Z), содержащую не менее семи логических операций. Построить таблицу истинности к ней. Применить СКНФ или СДНФ. Упростить по приведенному в презентации алгоритму. Построить новую схему.
• Нарисовать схему логического элемента с тремя логическими входами (X,Y,Z), содержащую не менее семи логических операций.
• Построить таблицу истинности к ней. Применить СКНФ или СДНФ.
• Упростить по приведенному в презентации алгоритму.
• Построить новую схему.

Ключ для проверки:

• Сv(BΛ ̚ А)
• СΛ ( ̚ Вv ̚ А)
• ̚ СΛ( ̚ Вv А)
• ̚ АΛ(Bv ̚ С)
• ̚ ВΛ(Сv ̚ А)
• ̚ Вv(СΛ ̚ А)
• ̚ Аv(BΛ ̚ С)