Презентация по информатике "Алгебра высказываний"

Еще живший в 384 - 322 г.г. до нашей эры древнегреческий ученый и философ Аристотель (Ἀριστοτέλης) пытался найти ответ на вопрос “Как мы рассуждаем”, изучал правила мышления. Он впервые дал систематическое изложение логики, подверг анализу человеческое мышление, его формы – понятие, суждение, умозаключение. Так возникла формальная логика.

Немецкий ученый и философ Готфрид - Вильгельм Лейбниц (Gottfried Wilhelm von Leibniz) (1646-1716) начал развивать идею формализации логики, размышляя о ее переводе "из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно".

Лейбниц мечтал создать особый язык для выражения мыслей в чистом виде - lingua mentalis, с помощью которого можно было бы математически строго выразить любую мысль. При этом он уделял особое внимание двоичной системе счисления, считая ее основой основ для любого счета.

Claude Elwood Shannon (1916 - 2001).

Является основателем теории информации, нашедшей применение в современных высокотехнологических системах связи. Шеннон внес огромный вклад в теорию вероятностных схем, теорию автоматов и теорию систем управления — области наук, входящие в понятие кибернетика.

Буль (Boole) Джордж (1815 — 1864) английский математик и логик. Не имея специального математического образования, в 1849 стал профессором математики в Куинс-колледже в Корке (Ирландия), где преподавал до конца жизни. Д. Буля почти в равной мере интересовали логика, математический анализ, теория вероятностей, этика Б. Спинозы, философские работы Аристотеля и Цицерона.

Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств  и т.д.).

МБОУ СОШ №7 п.Коммаяк

Кировского района

Ставропольского края

Учитель высшей

квалификационной категории

Куликова Татьяна Ивановна

Еще живший в 384 - 322 г.г. до нашей эры древнегреческий ученый и философ Аристотель (Ἀριστοτέλης) пытался найти ответ на вопрос “Как мы рассуждаем”, изучал правила мышления. Он впервые дал систематическое изложение логики, подверг анализу человеческое мышление, его формы – понятие, суждение, умозаключение. Так возникла формальная логика.

Немецкий ученый и философ Готфрид - Вильгельм Лейбниц (Gottfried Wilhelm von Leibniz) (1646-1716) начал развивать идею формализации логики, размышляя о ее переводе "из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно". Лейбниц мечтал создать особый язык для выражения мыслей в чистом виде - lingua mentalis, с помощью которого можно было бы математически строго выразить любую мысль. При этом он уделял особое внимание двоичной системе счисления, считая ее основой основ для любого счета.

Claude Elwood Shannon (1916 - 2001).

Является основателем теории информации, нашедшей применение в современных высокотехнологических системах связи. Шеннон внес огромный вклад в теорию вероятностных схем, теорию автоматов и теорию систем управления — области наук, входящие в понятие кибернетика.

Буль (Boole) Джордж (1815 — 1864) английский математик и логик. Не имея специального математического образования, в 1849 стал профессором математики в Куинс-колледже в Корке (Ирландия), где преподавал до конца жизни. Д. Буля почти в равной мере интересовали логика, математический анализ, теория вероятностей, этика Б. Спинозы, философские работы Аристотеля и Цицерона.

Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и т.д.).

Логика – это наука о формах и способах мышления

Формы мышления

понятие

суждение

(высказывание,

утверждение)

умозаключение

Понятие  - это форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других.

Понятие выражается одним или несколькими словами.

Понятие имеет две стороны: содержание и объем.

Например: треугольник, компьютер, персональный компьютер, стол, дом и т.п.

Суждения  - это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком, отношения между предметами или факт существования предмета и которая может быть либо истинной, либо ложной. Языковой формой выражения суждения является повествовательное предложение. Вопросительные и побудительные предложения суждениями не являются.

Суждения  рассматриваются не с точки зрения их смысла и содержания, а только с точки зрения их истинности или ложности. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных объектов. "Дважды два равно четырем" - истинное суждение, а вот "Процессор предназначен для печати" - ложное. Суждения могут быть простыми и сложными. "Весна наступила, и грачи прилетели" - сложное суждение, состоящее из двух простых.

КАКИЕ ИЗ ПРЕДЛОЖЕНИЙ ЯВЛЯЮТСЯ ВЫСКАЗЫВАНИЯМИ? ОПРЕДЕЛИТЕ ИХ ИСТИННОСТЬ

1. Число 6 – чётное.

Да

2. Посмотрите на доску.

Нет

3. Все роботы являются машинами.

Да

КАКИЕ ИЗ ПРЕДЛОЖЕНИЙ ЯВЛЯЮТСЯ ВЫСКАЗЫВАНИЯМИ? ОПРЕДЕЛИТЕ ИХ ИСТИННОСТЬ

4. У каждой лошади есть хвост.

Да

5. Внимание!

Нет

6. Кто отсутствует?

Нет

МОУ "Экономическая гимназия" Никифорова Л.Г,

Умозаключение

Пример 1:заключение на основании двух посылок:

Посылка: все буквы - знаки.

Посылка: «А» - это буква.

Заключение: буква «А» - это знак.

Пример 2:заключение на основании трех посылок:

Посылка: Буква – это часть слова.

Посылка: Слово – часть предложения.

Посылка: Предложение – часть текста.

Заключение: буква «А» - это текста.

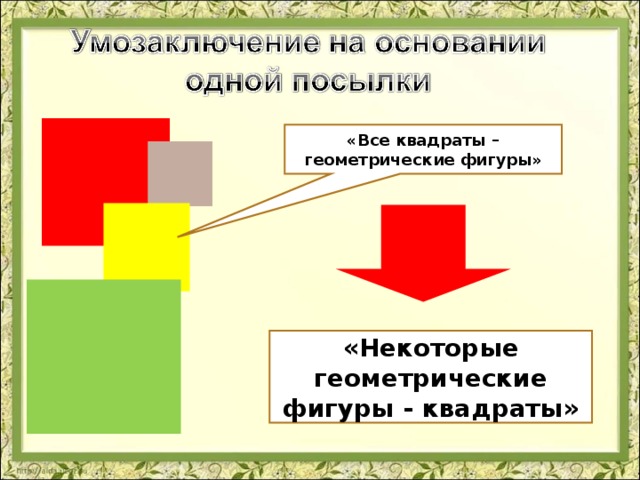
«Все квадраты – геометрические фигуры»

«Некоторые геометрические фигуры - квадраты»

Объектами алгебры логики являются высказывания.

Алгебру логики интересует только один факт – истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.

Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:

А= { Аристотель – основоположник

логики } ;

В= { На яблонях растут бананы } .

Истинному высказыванию ставится в соответствие 1, ложному – 0.

Таким образом, А=1, В=0.

Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции.

Логические операции задаются таблицами истинности и могут быть проиллюстрированы с помощью диаграмм Эйлера-Венна.

• в естественном языке соответствует союзу И;
• в алгебре высказываний обозначение & ;
• в языках программирования обозначение And .

Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Таблица истинности

А В А & В

0 0 0

0 1 0

1 0 0

1 1 1

Диаграмма Эйлера-Венна

• в естественном языке соответствует союзу ИЛИ;
• в алгебре высказываний обозначение V ;
• в языках программирования обозначение Or .

Дизъюнкция – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

Таблица истинности

А В А V В

0 0 0

0 1 1

1 0 1

1 1 1

Диаграмма Эйлера-Венна

• в естественном языке соответствует словам неверно, что… и частице не;
• в алгебре высказываний обозначение Ā ;
• в языках программирования обозначение Not .

Отрицание – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Таблица истинности

А Ā

0 1

1 0

Диаграмма Эйлера-Венна

• в естественном языке соответствует обороту если …, то …;
• обозначение  .

Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (1-ое высказывание) истинно, а следствие (2-ое высказывание) ложно.

Таблица истинности

А В А  В

0 0 1

0 1 1

1 0 0

1 1 1

• в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае;
• обозначение  , ~ .

Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Таблица истинности

А В А  В

0 0 1

0 1 0

1 0 0

1 1 1

Логические операции имеют следующий приоритет:

• действия в скобках; инверсия (отрицание); & ; V ;  ;  .
• действия в скобках;
• инверсия (отрицание);
• & ;
• V ;
•  ;
•  .

1. Найдите значения логических выражений:

а) ( 1 v 1 ) v ( 1 v O);

б) (( 1 v O) v 1 ) v 1 ;

в) (0 v 1) v (1 v 0);

г) (0 & 1) & 1;

е) (( 1 v O) & ( 1 & l)) & (O v 1 );

ж) (( 1 &O) v ( 1 &O)) v 1 ;

з) (( 1 & 1 ) v O) & (O v 1 );

и) ((0&0) v0) & ( 1 v 1 ).

2. Даны два простых высказывания:

А = {2 • 2 = 4}, В = {2 •  2 = 5}.

Какие из высказываний истинны:

а) А;     б) В; в) А&В;     г)AvB ; д) ¬ A ; е) A ^ В; ж) А ^ ¬В?

3.  Даны простые высказывания:

А = {Принтер — устройство ввода информации},

В = {Процессор — устройство обработки информации},

С = {Монитор — устройство хранения информации},

D = {Клавиатура — устройство ввода информации}.

Определите истинность высказывания: (A & B) & (C v D).   

B , б) B = A , которые будут принимать ложные значения.   2. Даны истинные высказывания А = «Карлсон хочет варенье» и В = «Карлсон летает на свежем воздухе». Составьте истинные высказывания вида A B .   3. Даны простые высказывания: А = {Принтер — устройство ввода информации}, В = {Процессор — устройство обработки информации}, С = {Монитор — устройство хранения информации}, D = {Клавиатура — устройство ввода информации}. Определите истинность составных высказываний: а) (AvB) (C& D );   б) А↔ В.   4. Даны простые высказывания: А = {53}, В = {2=3} и С = {4Определите истинность составных высказываний a) (A v B) & C = (A & C) v (B & C); б ) (A & B) v C ↔  (A v C) & (A &B ). " width="640"

1. Даны истинные высказывания: А= «на улице идет снег» и В = «нужно надеть шапку».

Составьте высказывания: а) А= B , б) B = A , которые будут принимать ложные значения.

2. Даны истинные высказывания А = «Карлсон хочет варенье» и В = «Карлсон летает на свежем воздухе». Составьте истинные высказывания вида A B .

3. Даны простые высказывания:

А = {Принтер — устройство ввода информации},

В = {Процессор — устройство обработки информации},

С = {Монитор — устройство хранения информации},

D = {Клавиатура — устройство ввода информации}.

Определите истинность составных высказываний:

а) (AvB) (C& D );   б) А↔ В.

4. Даны простые высказывания:

А = {53}, В = {2=3} и С = {4

Определите истинность составных высказываний

a) (A v B) & C = (A & C) v (B & C); б ) (A & B) v C ↔  (A v C) & (A &B ).

Сложные высказывания можно записывать в виде формул. Для этого простые логические высказывания нужно обозначить как логические переменные буквами и связать их с помощью знаков логических операций. Такие формулы называются логическими выражениями. Например:

Чтобы определить значение логического выражения необходимо подставить значения логических переменных в выражение и выполнить логические операции. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:      1. инверсия;      2. конъюнкция;      3. дизъюнкция;      4. импликация и эквивалентность. Для изменения указанного порядка выполнения логических операций используются круглые скобки.

Для каждого составного высказывания (логического выражения) можно построить таблицу истинности , которая определяет истинность или ложность логического выражения при всех возможных комбинациях исходных значений простых высказываний (логических переменных).

При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий:

1) записать выражение и определить порядок выполнения операций

2) определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (определяется по формуле Q=2 n , где n - количество входных переменных)

3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций)

4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных.

5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности

Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

Например, построим таблицу истинности для логической функции:

Количество входных переменных в заданном выражении равно трем (A,B,C) . Значит, количество входных наборов, а значит и строк Q=2 3 =8 . Количество столбцов равно 6 (3 переменные + 3 операции). Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C , промежуточных результатов и ( B V C ), а также искомого окончательного значения сложного арифметического выражения

A

B

C

B V C

A

B

0

0

C

0

0

0

0

1

0

1

B V C

1

0

1

0

1

1

0

0

1

1

1

1

0

1

1

A

B

0

C

0

0

0

0

0

1

1

1

B V C

0

1

0

0

1

1

1

0

1

1

0

1

1

1

1

1

0

0

1

0

1

1

1

1

1

0

0

1

0

1

0

1

0

0

0

1

0

1

0

Задание. Постройте таблицу истинности для данного логического выражения:

ТОЖДЕСТВЕННАЯ ИСТИНА

При всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

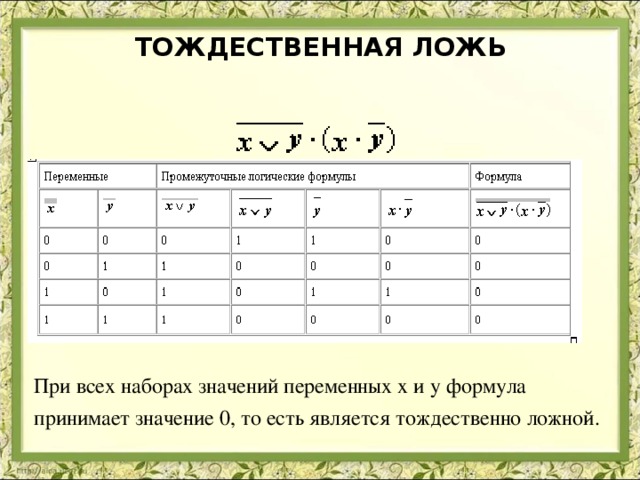
ТОЖДЕСТВЕННАЯ ЛОЖЬ

При всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.

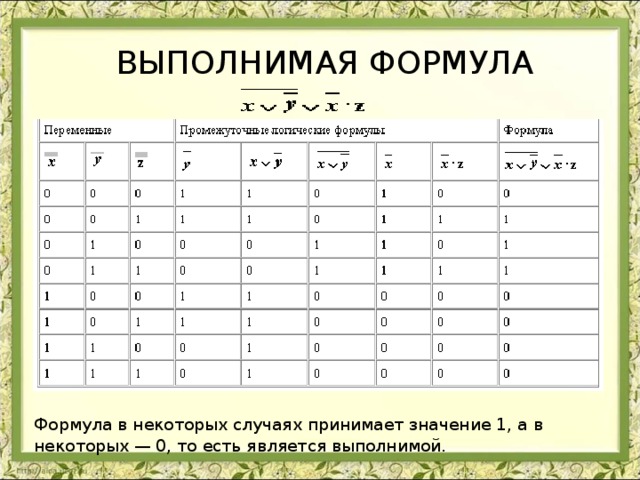
ВЫПОЛНИМАЯ ФОРМУЛА

Формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.

ДОМАШНЕЕ ЗАДАНИЕ:

1. Выучить определения, знать обозначения.

2. Даны высказывания:

А = {На улице светит солнце},

В = {На улице дождь},

С = {На улице пасмурная погода},

В = {На улице идет снег}. 

Составьте два сложных высказывания, одно из которых в любой ситуации всегда будет ложным, а другое истинным.

• Построить таблицу истинности следующих выражений :