Конспект урока по информатике.
Базовые логические операции. Логические выражения и таблицы истинности.
Предмет: информатика
Урок: 45 мин
Общие сведения: учебная тема - теоретическая часть: «Базовые логические операции. Логические выражения и таблицы истинности».
Цели урока:
образовательная: изучение базовых логических операций, порядок выполнения логических операций, построение логических выражений, таблицы истинности, алгоритм построения таблиц истинности.
развивающая: развитие интереса к предмету, умение делать выводы.
воспитательная: воспитание внимательности, дисциплинированности, эстетики при выполнении.
Ядро содержания обучения: понятия конъюнкция, дизъюнкция и инверсия; логическое выражение, таблица истинности (алгоритм построения).
Предварительная подготовка учащихся: актуализация опорных знаний.
Предварительная подготовка учителя: изучение материала урока, написание конспекта, подготовка примеров, разработка презентации.
Дидактические основания урока:
методы обучения: объяснительно-иллюстративный.
тип урока: комбинированный.
формы учебной работы учащихся: фронтальная работа.
Литература: для учителя – Угринович Н. Д. Информатика и информационные технологии. 10 –11 классы. М., 2003.; Бочкин А. И. Методика преподавания информатики. Мн., 1998. Для учеников - Угринович Н. Д. Информатика и информационные технологии. 10 –11 классы. М., 2003.
Техническая база кабинета:
Рабочее место преподавателя (РМП) в количестве – 1шт, видеопроектор, доска.
План урока:
Организационный момент (1 минута)
Актуализация опорных знаний (2 минуты)
Опрос домашнего задания (10 минут)
Объяснение нового материала (28 минут)
Информирование учащихся о домашнем задании и инструктаж по его выполнению (3 мин).
Итог (1 мин).
9. Содержательно деятельностный компонент:
Ход урока:
Здравствуйте, садитесь.
На прошлом уроке вы начали изучать математическую логику. Познакомились с таким понятием как высказывание. Давайте повторим: Каким оно может быть? ( Простые и составные) Приведите примеры простого высказывания и составного? А может ли высказывание быть выражено в форме вопросительного предложения? Как строятся составные высказывания? Какие значения могут принимать выражения? (истинные или ложные), например?
Хорошо, на дом вам был задан пункт 3.2 до пункта 3.2.1. Что основное вы выделили из домашнего задания?:
Для чего разработана алгебра высказываний? (алгебра высказываний разработана, чтобы можно было определить истинность или ложность составных высказываний, не вникая в их содержание) Сегодня среда и на улице оттепель или в классе горит свет или сегодня 2004 год и у нас последний урок
Как обозначаются логические переменные? (обозначаются прописными буквами латинского алфавита) A, B,C,D,E,W,Q…
Для чего нужны логические переменные? (они ставятся в соответствие суждениям (простым высказываниям)) A=сегодня четверг
Какие значения могут принимать логические переменные? (истина или ложь) А=Сегодня среда - 0 – ложь В= я веду урок у 11 А – 1 – истина
Что можно производить над высказываниями? (над высказываниями можно производить определенные логические операции, в результате получаются новые, составные высказывания)
Какие базовые логические операции наиболее часто используются для образования новых высказываний? (и, или, не)
Хорошо. Сегодня на уроке вы должны познакомиться с основными логическими операциями (и, или, не), их обозначениями, таблицами истинности, узнаете что такое логические выражения, что такое таблица истинности и как ее построить.
Откройте тетради и запишите тему сегодняшнего урока “Базовые логические операции. Логические выражения и таблицы истинности”.
Составные высказывания в алгебре логики записываются с помощью логических выражений. Существует несколько основных операций алгебры высказываний, при помощи которых строятся логические выражения. Давайте их рассмотрим.
Запишите : Основные логические операции.
1. КОНЪЮНКЦИЯ (связываю):
в естественном языке соответствует союзу и;
обозначение: & либо /\
в языках программирования обозначение: and;
иное название: логическое умножение.
Конъюнкция - это логическая операция, являющаяся истинной тогда и только тогда, когда оба исходных высказывания истинны.
Давайте посмотрим на примерах, откройте учебник на странице 126:
(1) 2*2=5 и 3*3=10 Истинно оно или нет?
(2) 2*2=5 и 3*3=9 А это? Почему?
(3) 2*2=4 и 3*3=10
(4)2*2=4 и 3*3=9
В приведенных примерах истинно только 4ое. Почему?
Пусть логическая переменная А = «идет снег», а В=(2*2=4) , тогда на основе этих высказываний при помощи логической операции конъюнкция получим составное высказывание F , F=А&В. Таким способом мы записали формулу функции логического умножения, аргументы которой логич переменные А и В, которые могут принимать значения истину или лжи. Сама функция логич умножения так же может принимать лишь два значения – истина или ложь.
Значение логич функции можно определить с помощью таблицы истинности данной функции, при всевозможных наборах ее аргументов, зарисуйте, в уч стр 127:
| А | В | А&В |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Вот пример: А = «Урок длится 40 минут» В = «2*2=3». Первое высказывание(А) истинно -1, а второе(В) ложно – 0, по таблице получается , что F=А&В – ложно – 0 .
2. ДИЗЪЮНКЦИЯ (различаю):
в естественном языке соответствует союзу или;
обозначение: ;
в языках программирования обозначение: or;
иное название: логическое сложение.
Дизъюнкция - это логическая операция , являющаяся ложной тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
На странице 127 примеры:
(1) 2*2=5 или 3*3=10 это высказывание истинно?
(2) 2*2=5 или 3*3=9
(3) 2*2=4 или 3*3=10
(4) 2*2=4 или 3*3=9
Пусть 2*2=5 – высказывание А, а высказывание В=3*3=9, опять же на основе этих высказываний только теперь при помощи логической операции дизъюнкция получим составное высказывание F=А\/В – это и есть формула функции логического сложения, аргументами которой являются логические переменные А и В.
Значение логич функции можно так же определить с помощью таблицы истинности данной функции, при всевозможных наборах ее аргументов, зарисуйте ее, стр 128:
| А | В | А В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Например: «Сейчас ночь или идет урок информатики», разделим это сложное высказывание на простые, получается как? А = «Сейчас ночь» - ложь – 1 , В = «идет урок информатики» - истина – 0; смотрим по таблице А=0, В=1, получается что А\/В=1 – истина;
Теперь у нас осталась последняя основная логическая операция – инверсия.
3. ИНВЕРСИЯ (переворачиваю):
в естественном языке соответствует словам "Неверно, что... " и частице не;
обозначение: 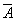 ;
;
в языках программирования обозначение: not;
иное название: отрицание.
Отрицание - это логическая операция, заключающаяся в том, что исходное высказывание отрицается.
Например: «сегодня четверг» – истина -1, тогда F= «сегодня не четверг»
Так же как и у двух предыдущих логических операций существует таблица истинности, зоарисуйте, стр 129:
| A | 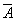
|
| 0 | 1 |
| 1 | 0 |
По таблице легко определить истинность высказывания: например А= «в 11А 27 человек» - ложно – 1, по таблице получим F=1, «в 11А не 27 человек» - истинно.
С основными логическими операциями познакомились. Как думаете, должен ли существовать порядок выполнения логических операций?
Запишите, порядок выполнения логических операций:
инверсия
конъюнкция
дизъюнкция
для изменения указанного порядка могут использоваться скобки
как в математике, сначала выполняется то, что находится в скобках.
А теперь запишите: Каждое составное высказывание можно выразить в виде формулы – логического выражения. В логическое выражение входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции. Давайте рассмотрим пример на стр 130, запишите:
1. «(2*2=5 или 2*2=4) и (2*25 или 2*24)»
Это составное высказывание, из каких простых оно состоит?
2. Выделяем простые высказывания А= «2*2=5» В= «2*2=4» , теперь мы можем составное высказывание записать так:
3. «(А или В) и (неА или неВ)»
4. F=(A\/B)&(неА \/неВ)
5. F=(A\/B)&(неА \/неВ) = (0\/1)&(1\/0)=1&1=1
Для любого логического выражения достаточно просто построить таблицу истинности. Таблицу, показывающую, какие значения принимает составное высказывание, называют таблицей истинности составного высказывания. Запишите это определение.
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице m = 2n;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов в таблице: число переменных плюс число операций;
6. провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Давайте попробуем построить таблицу истинности для последнего примера:
2 переменные - количество строк = 4;
теперь подсчитаем кол-во столбцов = кол-во переменных (2) + кол-во логических операций…сколько в этом примере операций? (5)
Теперь строим таблицу, 5 строк, 1ая отводиться под заголовки столбцов, и 7 строк. Вносим в таблицу всевозможные наборы значений исходных логич переменных, каких переменных? (А и В)
Заполняем таблицу по столбцам, выполняя операции в необходимой последовательности и в соответствии с их таблицами истинности.
У нас получилась таблица истинности, по ней теперь можно определить значение логических функции для любого набора значений логических переменных.
Это понятно?
Ребята, сегодня на уроке вы изучили такие базовые операции как: конъюнкция, дизъюнкция и инверсия; на примере научились составлять логические выражения и таблицу истинности. Кратко напомните ключевые моменты этого урока?
Теперь откройте дневники и запишите домашнее задание: самостоятельно изучите параграф3.3 («Равносильные логические выражения»), прочитайте еще раз параграф 3.2.1 – конец параграфа 3.3. На следующем уроке спрошу основные понятия.
Выполните задания:
1) Определите истинность простых высказываний:
А = {Принтер – устройство ввода информации},
В = {Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.
Определите истинность составных высказываний:
а) (А&В) (C D); б) (А&В) /\ (C D);
в) (А В) /\ (C D); г) 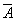 /\
/\ 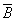 .
.
2) Найдите значения логических выражений:
а) (11)(10); 1
б) ((10)1)1; 1
в) (01)(10); 1
г) (0&1)&1; 0
4) Для формулы A&(B 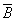 &
& 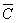 ) построить таблицу истинности алгебраически. Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8. Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.
) построить таблицу истинности алгебраически. Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8. Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.
Спасибо за внимание, урок окончен. До свидания!

 Получите свидетельство
Получите свидетельство Вход
Вход












 Разработка урока по информатике "Базовые логические операции. Логические выражения и таблицы истинности" (78 КB)
Разработка урока по информатике "Базовые логические операции. Логические выражения и таблицы истинности" (78 КB)
 0
0 1081
1081 151
151 Нравится
0
Нравится
0


