Повторение. Решение тригонометрических уравнений

Овчинникова Н.В., учитель математики,

МАОУ «СОШ №2», г.Краснотурьинск, Свердловской обл.

Решение тригонометрических уравнений

Повторение изученного материала.

Простейшие тригонометрические уравнения

Уравнения 1 и 2 имеют решения, если а  -1; 1 

• sin х = a

x = arcsin a + 2  k

x = (  - arcsin a) + 2  k, к  Z

2. cos х = a

x =  arccos a + 2  k, k  Z

3. tg х = a

x = arctg a +  k , k  Z

Если в 1 и 2 уравнениях вместо а стоят числа -1, 0, 1, то надо применять частные случаи решения этих уравнений.

Надо помнить:

• arcsin (-a) = -arcsin a

• arccos(-a) =  - arccos a

• arctg (-a) = - arctg a

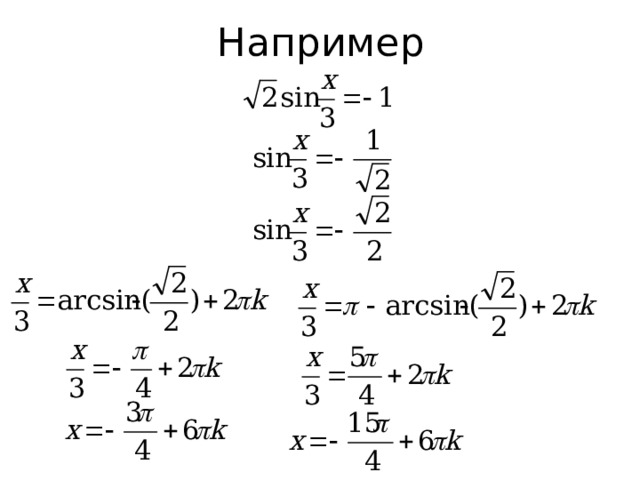
Например

Виды тригонометрических уравнений.

• Уравнения, сводящиеся к квадратным

• Однородные тригонометрические уравнения (первой и второй степеней)

• Уравнения, решаемые разложением левой части на множители.

Уравнения, сводящиеся к квадратным

Уравнения, сводящиеся к квадратным

Однородные тригонометрические уравнения

Второй степени

Первой степени

a  sinx + b  cosx = 0

Решаются делением обеих частей уравнения на cos x

Например

sinx = 2cosx

sinx - 2cosx = 0

tgx – 2 = 0

tgx = 2

x = arctg 2 +  k

Ответ: arctg 2 +  k, k  Z

Решаются делением обеих частей уравнения на

Например

Если произведение нескольких множителей равно нулю , то хотя бы один из этих множителей равен нулю .

Уравнения, решаемые разложением

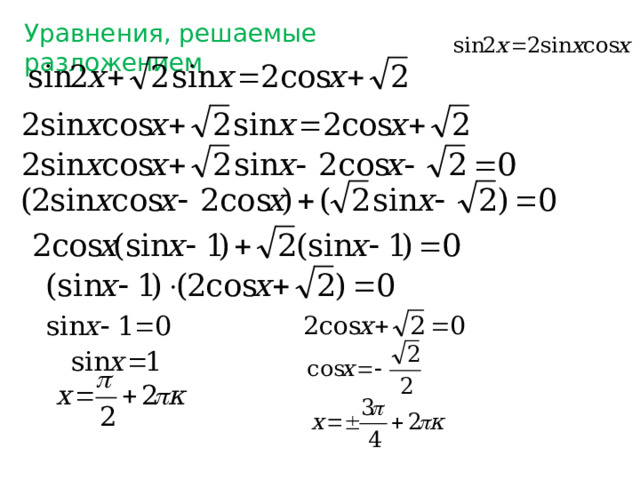
Уравнения, решаемые разложением

Домашнее задание.

• Стр.198, задания раздела «Проверь себя»

Выучить решения простейших тригонометрических уравнений (не забудьте про частные случаи)