Однородные тригонометрические уравнения
Колтакова Ирина Сергеевна ,учитель математики МБОУСОШ 1 г. Королев
ГМО Математика
![]()
Цели урока:
1) Обучающие – познакомить учащихся с однородными уравнениями, рассмотреть методы их решения, способствовать формированию навыков решения ранее изученных видов тригонометрических уравнений.
2) Развивающие – развивать творческую активность учащихся, их познавательную деятельность, логическое мышление, память, умение работать в проблемной ситуации, добиваться умения правильно, последовательно, рационально излагать свои мысли, расширить кругозор учащихся, повышать уровень их математической культуры.
3) Воспитательные –формировать умение грамотно и аккуратно выполнять математические записи, воспитывать активность, содействовать побуждению интереса к математике.
Тип урока: комбинированный.
Оборудование:
Карточки для шести учащихся.
Карточки для самостоятельной и индивидуальной работы учащихся.
Стенды «Решение тригонометрических уравнений», «Числовая единичная окружность»
Презентация к уроку (Приложение 1).
Ход урока
1. Организационный этап (2 минуты)
Взаимное приветствие; проверка подготовленности учащихся к уроку (рабочее место, внешний вид); организация внимания.
Учитель сообщает учащимся тему урока, цели (слайд 2) и поясняет, что во время урока будет использоваться тот раздаточный материал, который находится на партах.
2. Повторение теоретического материала (15 минут)
Задания на перфокартах (6 человек). Время работы по перфокартам – 10 мин (Приложение 2)
Решив задания, учащиеся узнают, где применяются тригонометрические вычисления. Получаются такие ответы: триангуляция (техника, позволяющая измерять расстояния до недалеких звезд в астрономии), акустика, УЗИ, томография, геодезия, криптография.
(слайд 3)
Фронтальный опрос.
Какие уравнения называются тригонометрическими?
Какие виды тригонометрических уравнений вы знаете?
Какие уравнения называются простейшими тригонометрическими уравнениями?
Какие уравнения называются квадратными тригонометрическими?
Сформулировать определение арксинуса числа а.
Сформулировать определение арккосинуса числа а.
Сформулировать определение арктангенса числа а.
Сформулировать определение арккотангенса числа а.
Игра «Отгадайте зашифрованное слово»
Когда-то Блез Паскаль сказал, что математика – наука настолько серьёзная, что нельзя упускать случая, сделать её немного более занимательной. Поэтому я предлагаю поиграть. Решив примеры, определите последовательность цифр, по которой составлено зашифрованное слово. По латыни это слово означает «синус». (слайд 4)
1) arc tg 1
2) arc tg (-√3)
3) arc tg 0
4) tg (arc cos (1/2))
5) tg (arc ctg √3)
| Б | 1/√3 |
| И | π/4 |
| З | - π/3 |
| Т | π/6 |
| Г | 0 |
| С | 2 π |
| И | √3 |
Ответ: «Изгиб»
Игра «Рассеянный математик»
На экран проектируются задания для устной работы:
Проверьте правильность решения уравнений. (правильный ответ появляется на слайде после ответа учащегося). (слайд 5)
| | Ответы с ошибками | Правильные ответы |
| cos x = 1/2 | х = ±π/6+2πn | х = ±π/3+2πn |
| sinx = √3/2 | х = π/3+πn | х = (-1)nπ/3+πn |
| tg x = π/4 | х = 1+πn | tg x =1, х = π/4+πn |
| cos x = √3/2 | х = ±π/6+πn | х = ±π/6+2πn |
| sin x = 1/3 | х = (-1)n arcsin1/3+ 2πn | х = (-1)n arcsin1/3+ πn |
| cos x = -√3/2 | х = ±π/6+2πn | х = ±5π/6+2πn |
| cos x = π/3 | х = ±1/2+2πn | cos x = 1/2, х = ±π/3+2πn |
Проверка домашнего задания.
Преподаватель установливает правильность и осознанность выполнения домашнего задания всеми учащимися; выявляет пробелы в знаниях; совершенствует знания, умения и навыки учащихся в области решения простейших тригонометрических уравнений.
1 уравнение. Учащийся комментирует решение уравнения, строки которого появляются на слайде в порядке следования комментария). (слайд 6)
√3tg2x = 1;
tg2x =1/√3;
2х= arctg 1/√3 +πn, n ∈Z.
2х= π/6 +πn, n ∈Z.
х= π/12 +π/2n, n ∈Z.
2 уравнение. Решение записывается учащимся на доске.
2 sin2x + 3 cosx = 0.
3. Актуализация новых знаний (3 минуты)
Учащиеся по просьбе учителя вспоминают способы решения тригонометрических уравнений. Они выбирают те уравнения, которые уже умеют решать, называют способ решения уравнения и получившийся результат. Ответы появляются на слайде. (слайд 7) .
Введение новой переменной:
№1. 2sin2x – 7sinx + 3 = 0.
Пусть sinx = t, тогда:
2t2 – 7t + 3 = 0.
Разложение на множители:
№2. 3sinx cos4x – cos4x = 0;
сos4x(3sinx – 1) = 0;
cos4x = 0 или 3 sinx – 1 = 0; …
№3. 2 sinx – 3 cosx = 0,
№4. 3 sin2x – 4 sinx cosx + cos2x = 0.
Преподаватель: Последние два вида уравнений вы решать еще не умеете. Оба они одного вида. Их нельзя свести к уравнению относительно функций sinx или cosx. Называются однородными тригонометрическими уравнениями. Но только первое – однородное уравнение первой степени, а второе – однородное уравнение второй степени. Сегодня на уроке предстоит познакомиться с такими уравнениями и научиться их решать.
4. Объяснение нового материала (25 минут)
Преподаватель дает учащимся определения однородных тригонометрических уравнений, знакомит со способами их решения.
Определение. Уравнение вида a sinx + b cosx =0, где a ≠ 0, b ≠ 0 называется однородным тригонометрическим уравнением первой степени. (слайд 8)
Примером такого уравнения является уравнение №3. Выпишем общий вид уравнения и проанализируем его.
а sinx + b cosx = 0.
Если cosx = 0, то sinx = 0.
– Может ли получиться такая ситуация?
– Нет. Получили противоречие основному тригонометрическому тождеству.
Значит, cosx ≠ 0. Выполним почленное деление на cosx:
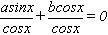
а · tgx + b = 0
tgx = –b / а – простейшее тригонометрическое уравнение.
Вывод: Однородные тригонометрические уравнения первой степени решаются делением обеих частей уравнения на cosx (sinx).
Например: 2 sinx – 3 cosx = 0,
Т.к. cosx ≠ 0, то
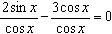
2tgx – 3 = 0;
tgx = 3/2;
х = arctg (3/2) +πn, n ∈Z.
Определение. Уравнение вида a sin2x + b sinx cosx + c cos2x = 0 , где a ≠ 0, b ≠ 0, c ≠ 0 называетсятригонометрическим уравнением второй степени. (слайд 8)
Примером такого уравнения является уравнение №4. Выпишем общий вид уравнения и проанализируем его.
a sin2x + b sinx cosx + c cos2x = 0.
Если cosx = 0, то sinx = 0.
Опять получили противоречие основному тригонометрическому тождеству.
Значит, cosx ≠ 0. Выполним почленное деление на cos2x:
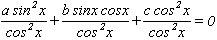
а tg2x + b tgx + c = 0 – уравнение, сводящееся к квадратному.
Вывод: Однородные тригонометрические уравнения второй степени решаются делением обеих частей уравнения на cos2x (sin2x).
Например: 3 sin2x – 4 sinx cosx + cos2x = 0.
Т.к. cos2x ≠ 0, то
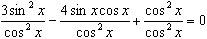
3tg2x – 4 tgx + 1 = 0 (Предложить ученику выйти к доске и дорешать уравнение самостоятельно).
Замена: tgx = у. 3у2– 4 у + 1 = 0
D = 16 – 12 = 4
y1 = 1 или y2 = 1/3
tgx = 1 или tgx = 1/3
tgx = 1:
x = arctg (1/3) + πn, n ∈Z.
tgx = 1/3:
х = arctg1 + πn, n ∈Z.
x = π/4 + πn, n ∈Z.
5. Этап проверки понимания учащимися нового материала (1 мин.)
Выберите лишнее уравнение:
sinx = 2cosx; 2sinx + cosx = 2;
√3sinx + cosx = 0; sin2x – 2 sinx cosx + 4cos2x = 0;
4cosx + 5sinx = 0; √3sinx – cosx = 0.
(слайд 9)
6. Закрепление нового материала (24 мин).
Учащиеся вместе с отвечающими у доски решают уравнения на новый материал. Задания написаны на слайде в виде таблицы. При решении уравнения открывается соответствующая часть картинки на слайде. В результате выполнения 4-х уравнений перед учащимися открывается портрет математика, оказавшего значительное влияние на развитие тригонометрии. (ученики узнают портрет Франсуа Виета – великого математика, внесшего большой вклад в тригонометрию, открывшего свойство корней приведенного квадратного уравнения и занимавшегося криптографией). (слайд 10)
1) √3sinx + cosx = 0,
Т.к. cosx ≠ 0, то
√3tgx + 1 = 0;
tgx = –1/√3;
х = arctg (–1/√3) + πn, n ∈Z.
х = –π/6 + πn, n ∈Z.
2) sin2x – 10 sinx cosx + 21cos2x = 0.
Т.к. cos2x ≠ 0, то tg2x – 10 tgx + 21 = 0
Замена: tgx = у.
у2 – 10 у + 21 = 0
у1 = 7 или у2 = 3
tgx = 7 или tgx = 3
tgx = 7:
х = arctg7 + πn, n ∈Z
tgx = 3:
х = arctg3 + πn, n ∈Z
3) sin22x – 6 sin2x cos2x + 5cos22x = 0.
Т.к. cos22x ≠ 0, то 3tg22x – 6tg2x +5 = 0
Замена: tg2x = у.
3у2 – 6у + 5 = 0
D = 36 – 20 = 16
у1= 5 или у2 = 1
tg2x = 5 или tg2x = 1
tg2x = 5:
2х = arctg5 + πn, n ∈Z
х = 1/2 arctg5 + π/2 n, n ∈Z
tg2x = 1:
2х = arctg1 + πn, n ∈Z
х = π/8 + π/2 n, n ∈Z
4) 6sin2x + 4 sin(π-x) cos(2π-x) = 1.
6sin2x + 4 sinx cosx = 1.
6sin2x + 4 sinx cosx – sin2x – cos2x = 0.
5sin2x + 4 sinx cosx – cos2x = 0.
Т.к. cos2x ≠0, то 5tg2x + 4 tgx –1 = 0
Замена: tg x = у.
5у2 + 4у – 1 = 0
D = 16 + 20 = 36
у1 = 1/5 или у2 = –1
tg x = 1/5 или tg x = –1
tg x = 1/5:
х = arctg1/5 + πn, n ∈Z
tg x = –1:
х = arctg(–1) + πn, n ∈Z
х = –π/4 + πn, n ∈Z
Дополнительно (на карточке):
Решить уравнение и, выбрав один вариант из четырех предложенных, отгадать имя математика, который вывел формулы приведения:
2sin2x – 3 sinx cosx – 5cos2x = 0.
Варианты ответов:
х = arctg2 + 2πn, n ∈Z х = –π/2 + πn, n ∈Z – П.Чебышев
х = arctg 12,5 + 2πn, n ∈Z х = –3π/4 + πn, n ∈Z – Евклид
х = arctg 5 + πn, n ∈Z х = –π/3 + πn, n ∈Z – Софья Ковалевская
х = arctg2,5 + πn, n ∈Z х = –π/4 + πn, n ∈Z – Леонард Эйлер
Правильный ответ: Леонард Эйлер.
7. Дифференцированная самостоятельная работа ( 8 мин.)
Великий математик и философ более 2500 лет назад подсказал способ развития мыслительных способностей. «Мышление начинается с удивления» – сказал он. В правильности этих слов мы сегодня неоднократно убеждались. Выполнив самостоятельную работу по 2-м вариантам, вы сможете показать, как усвоили материал и узнать имя этого математика. Для самостоятельной работы используйте раздаточный материал, который находится у вас на столах. Вы можете сами выбрать одно из трех предложенных уравнений. Но помните, что решив уравнение, соответствующее желтому цвету, вы сможете получить только «3»,решив уравнение, соответствующее зеленому цвету – «4», красному цвету – «5». (Приложение 3)
Какой бы уровень сложности не выбрали учащиеся, после правильного решения уравнения у первого варианта получается слово «АРИСТ», у второго – «ОТЕЛЬ». На слайде получается слово: «АРИСТ—ОТЕЛЬ». (слайд 11)
Листочки с самостоятельной работой сдаются на проверку. (Приложение 4)
8. Запись домашнего задания (1 мин)
Д/з: §7.17. Составить и решить 2 однородных уравнения первой степени и 1 однородное уравнение второй степени (используя для составления теорему Виета). (слайд 12)
9. Подведение итогов урока, выставление оценок (2 минуты)
Учитель еще раз обращает внимание, на те типы уравнений и те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их.
Учащиеся отвечают на вопросы:
С каким видом тригонометрических уравнений мы познакомились?
Как решаются эти уравнения?
Учитель отмечает наиболее успешную работу на уроке отдельных учащихся, выставляет отметки.
10


 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по математике "Однородные тригонометрические уравнения" (41.84 КB)
Конспект урока по математике "Однородные тригонометрические уравнения" (41.84 КB)
 0
0 601
601 90
90 Нравится
0
Нравится
0


