Понятие производной

ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ

ПОНЯТИЕ ПРОИЗВОДНОЙ

Сколько всего лиц?

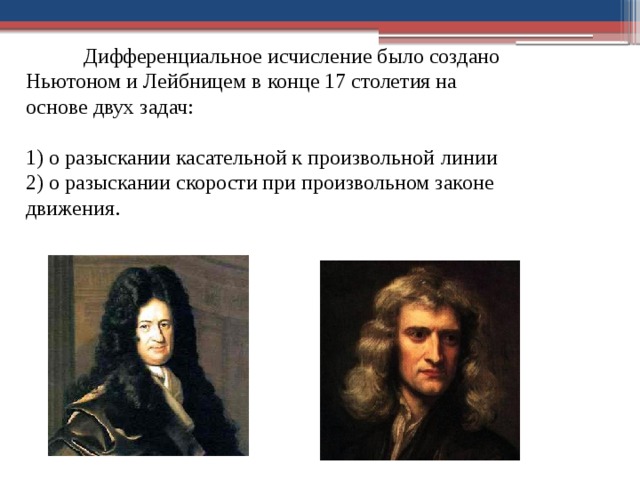
Дифференциальное исчисление было создано

Ньютоном и Лейбницем в конце 17 столетия на

основе двух задач:

1) о разыскании касательной к произвольной линии

2) о разыскании скорости при произвольном законе

движения .

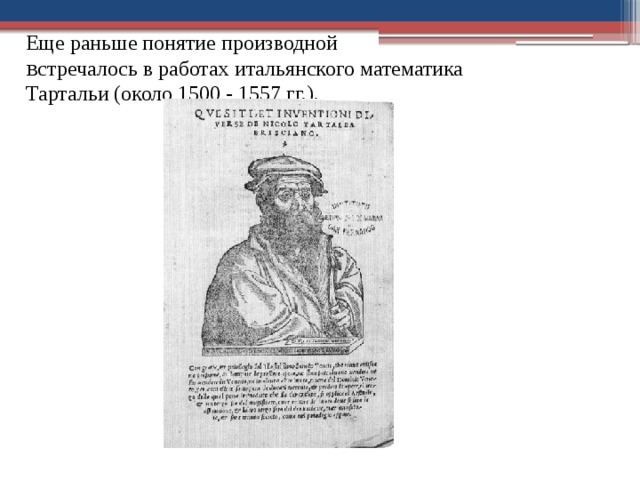
Еще раньше понятие производной

в стречалось в работах итальянского математика

Тартальи (около 1500 - 1557 гг.).

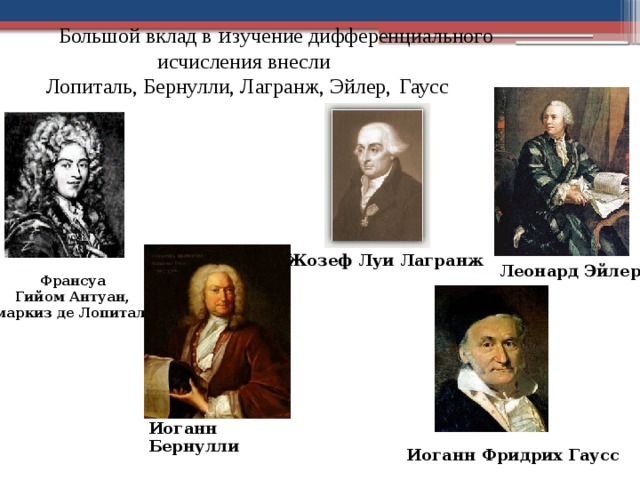
Большой вклад в и зучение дифференциального

исчисления внесли

Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс

Жозеф Луи Лагранж

Леонард Эйлер

Франсуа Гийом Антуан, маркиз де Лопиталь

Иоганн Бернулли

Иоганн Фридрих Гаусс

5

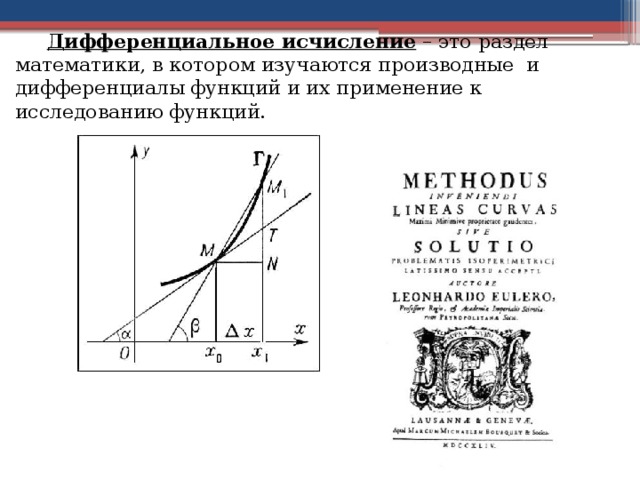
Дифференциальное исчисление – это раздел математики, в котором изучаются производные и дифференциалы функций и их применение к исследованию функций.

5

Термин « производная » является буквальным переводом на русский язык французского слова derivee , которое ввёл в 1797 году Ж. Лагранж . Он же ввёл современные обозначения:

Лейбниц говорил о дифференциальном отношении и обозначал производную как

Такое обозначение есть и в современной литературе.

5

Производная одно из фундаментальных понятий математики.

Оно возникло в XVII в. в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь для определения скорости прямолинейного движения и построения касательной к кривой.

5

Используя методы дифференциального исчисления английский астроном, математик Эдмон Галлей ещё в XVII веке предсказал возвращение кометы Галлея.

В 1705 году Эдмонд Галлей предсказал, что комета, которую наблюдали в 1531, 1607 и 1682 годах, должна возвратиться в 1758 году. Комета действительно возвратилась, как было предсказано, и позже была названа в его честь.

5

• Комета Галлея вернется во внутреннюю Солнечную систему в следующий раз в 2061 году.

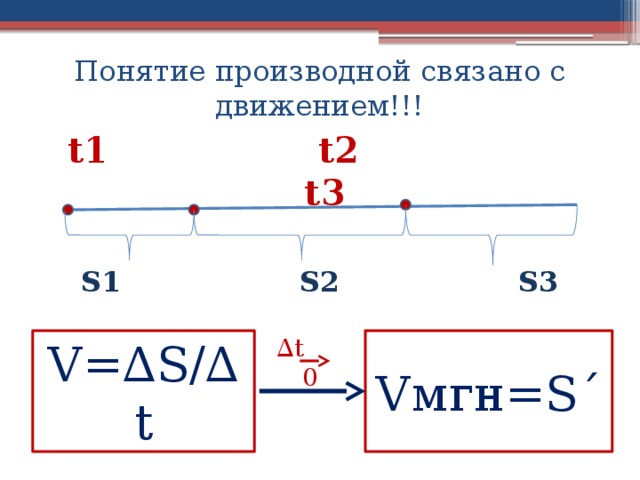
Понятие производной связано с движением!!!

t1 t2 t3

S1 S2 S3

V=∆S/∆t

Vмгн=S´

∆ t 0

• Что такое аргумент?
• Что такое функция?
• Какие функции вы знаете?

• Пусть  x  – аргумент функции  f(x)  и  - ∆Х малое число, отличное от нуля.

  (читается «дельта икс») называют 

приращением аргумента функции

∆ Х=Х-Х 0

• Разность 

∆ f=f(x 0 + ∆x)-f(x)

называют  приращением функции  f(x) , соответствующем данному приращению аргумента

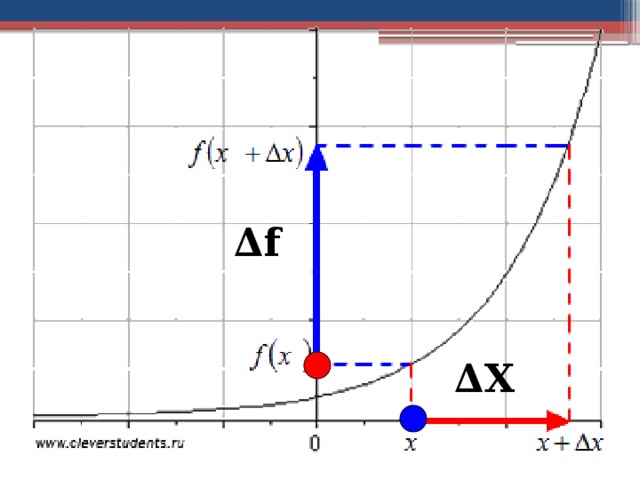
∆ f

∆ Х

Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю.

f′(x)-читается:

« эф штрих от икс»

Производная также обозначается

• у ′, у ′(х), f′, f′(x),

,   

.

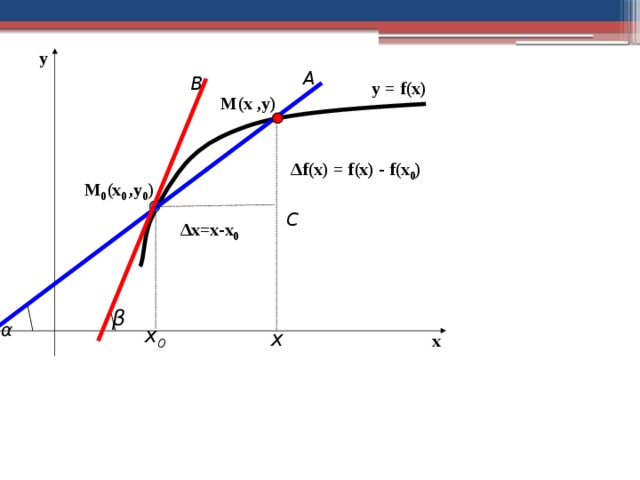
y

А

В

y = f(x)

М(х ,у)

∆ f(x) = f(x) - f(x 0 )

М 0 (х 0 ,у 0 )

С

∆ х=х-х 0

β

α

x 0

x

x

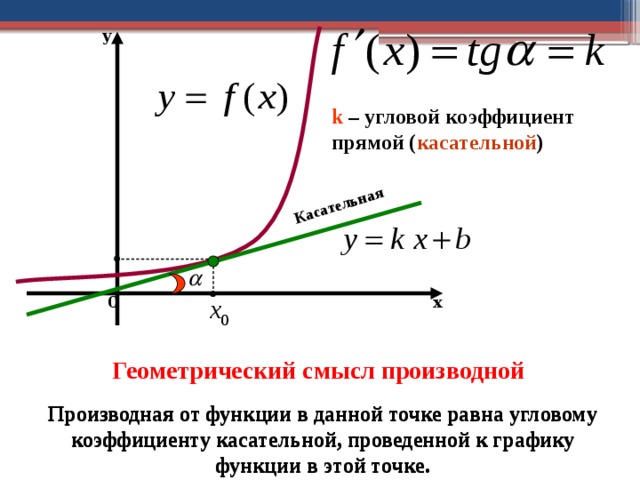
Касательная

y

k – угловой коэффициент прямой ( касательной )

0

х

Геометрический смысл производной

Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Физический смысл производной

• Производная пути по времени есть скорость
• S′(t)=V(t)

Производной

Геометрический смысл производной

• функции в данной точке называется _________ отношения _________функции в этой точке к приращению ____________, когда приращение аргумента стремится к________.

• Производная от функции в данной точке равна ______________________________________касательной, проведенной к ___________ функции в этой точке.

ЗАПОМНИТЕ

• Операция нахождения производной называется дифференцированием

• Производная функции в точке -это число

• Производная функции на отрезке -это функция

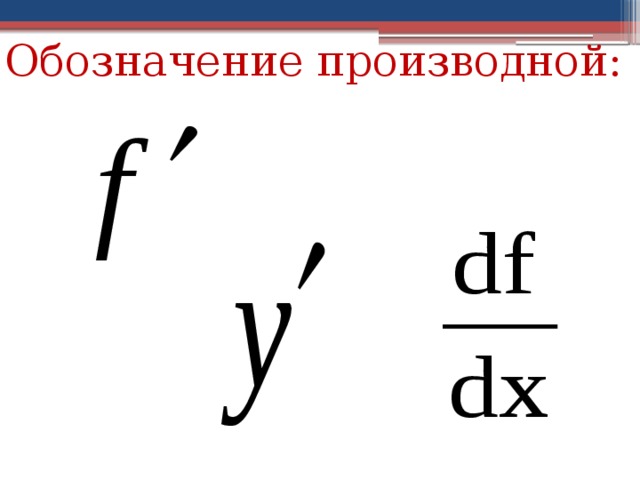
Обозначение производной:

.

В данной функции от x, нареченной игреком

Вы фиксируете x, отмечая индексом

Придаете вы ему тотчас приращение

Тем у функции самой вызвав изменение

Приращений тех теперь взявши отношение

Пробуждаете к нулю у стремление

Предел такого отношения вычисляется

Он ………… в науке называется

Как найти производную функции?

МОЗГОВОЙ ШТУРМ

Найдем производную функции f(x)=x²

• 1. Дадим х приращение ∆х
• 2. Тогда ∆f(x)=f(x 0 + ∆х)-f(x 0 )
• ∆ f(x)= (x 0 + ∆х)²-x 0 ² =
• =x 0 ²+2 x 0 ∆х+ ∆х²-x 0 ² =
• =2 x 0 ∆х+ ∆х²

• Итак: ∆f(x)= 2 x 0 ∆х+ ∆х²

Найдем производную функции f(x)=x²

• 3. Найдем разностное отношение:

∆ f(x) 2 x 0 ∆х+ ∆х²

=

∆ x ∆х

=2x 0 + ∆x

Найдем производную функции f(x)=x²

• 4. Найдем предел разностного отношение:

∆ f(x) 2 x 0 0+ ∆х²

2x 0 + ∆x=2x 0 +0=2x 0

lim

∆ х 0

=

∆ x ∆х

Производная функции f(x)=x² в точке х 0 равна 2х 0

Производная функции f(x)=x² в на отрезке равна 2х

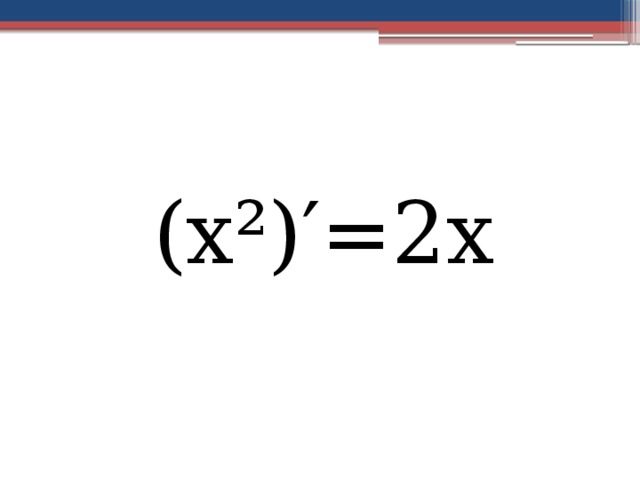
(х²)′=2х

Найдите производную функции f(x)=x³

• (а+b)³=a³+3a²b+3ab²+b³

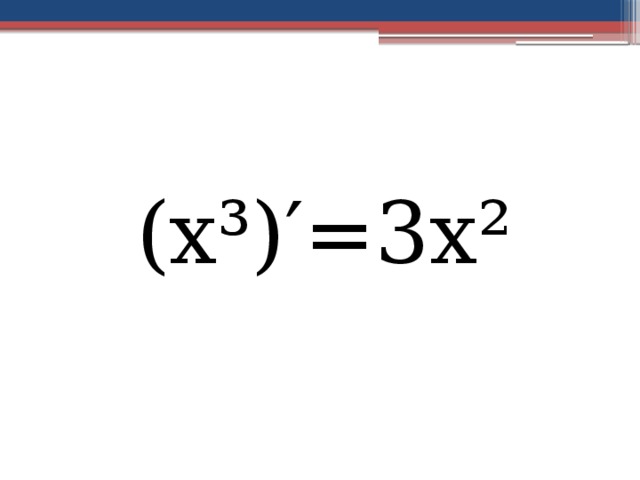
(х³)′=3х²

Найдите производную функции f(x)=x ⁵ Бином Ньютона

Биномиальные коэффициенты есть

коэффициэнты разложения многочлена

по степеням x и y

Найдите производную функции f(x)=x ⁵

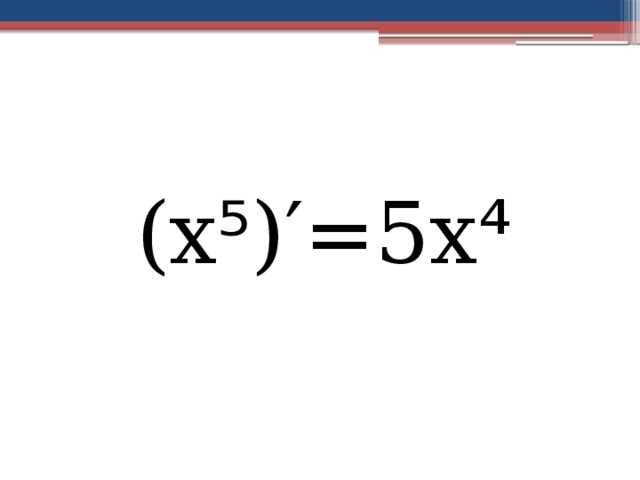
(х ⁵ )′=5х ⁴

Вывод

ФОРМУЛА

• (х²)′=2х
• (х³)′=3х²
• (х ⁴) ′=?
• (х ⁵ )′=5х ⁴
• (х ⁶) ′=?

• (х n )′=nx n-1

f′(x)= tgα=k

S′(t)=V(t)

(х n )′=nx n-1

Домашнее задание: знать ответы на вопросы

• 1) Приращение аргумента
• 2) Приращение функции
• 3) Производная
• 4) Геометрический смысл производной
• 5) Физический смысл производной
• 6) (х n )′=

Задания на повторения

• Подготовка к экзамену