Площадь треугольника.

Теорема о площади треугольника

• Перечислите формулы, применяемые при вычислении площади треугольника

Формулы площади треугольника

• , где а, в - катеты прямоугольного треугольника
• , где а - основание треугольника, h- высота

р- полупериметр,

а,в,с - стороны треугольника

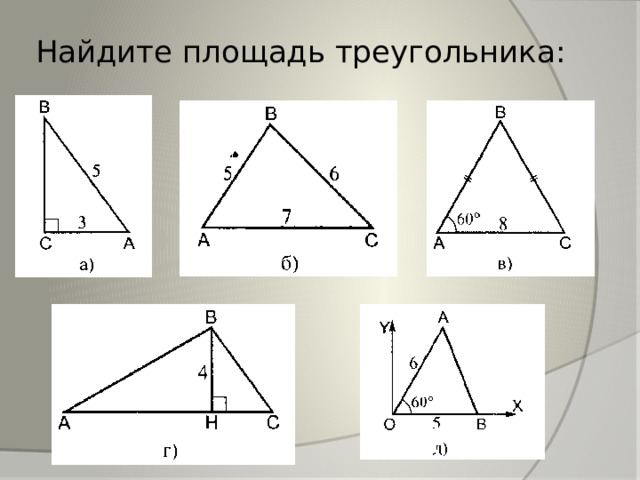
Найдите площадь треугольника:

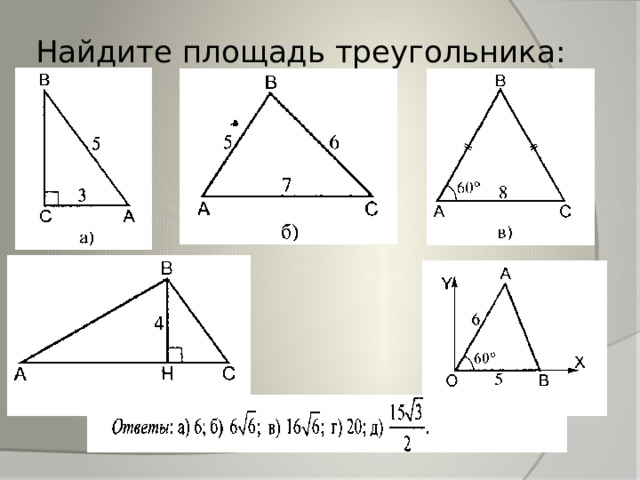
Найдите площадь треугольника:

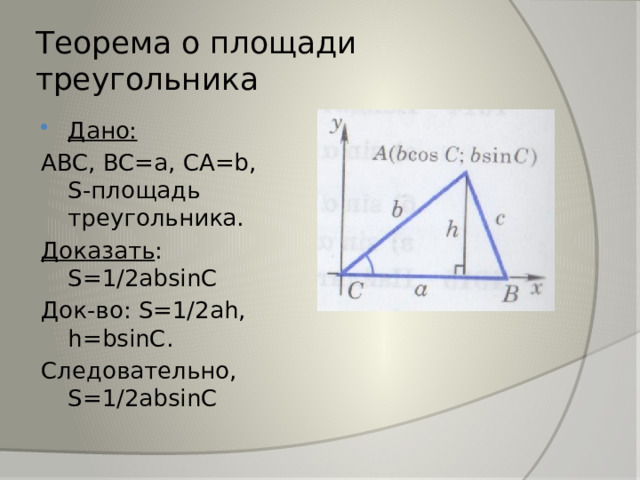
Теорема о площади треугольника

• Дано:

ABC, BC=a, CA=b, S-площадь треугольника.

Доказать : S=1/2absinC

Док-во: S=1/2ah, h=bsinC.

Следовательно, S=1/2absinC

Формула нахождения площади треугольника

Решение задач

• № 1020(а), 1024(а)

Дополнительная задача:

• Найдите площадь равнобедренного треугольника с углом при основании 15 и боковой стороной, равной 5см.
• В треугольнике АВС АВ=4, ВС=6, ВD -биссектриса, угол АВС=45 . Найдите площадь треугольников АВD и СВD

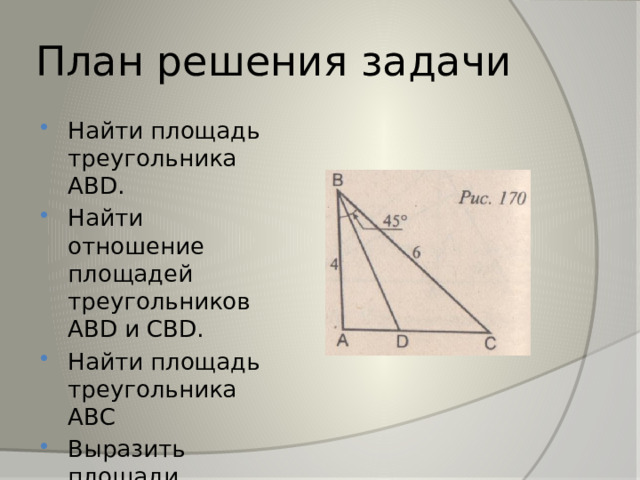
План решения задачи

• Найти площадь треугольника АВD.
• Найти отношение площадей треугольников АВD и СВD.
• Найти площадь треугольника АВС
• Выразить площади треугольников

Подготовка к ГИА

• Задачи:

1. В параллелограмме ABCD AB=6, AD=4, sinA=0,8. Найдите большую высоту параллелограмма.

2. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону трапеции.

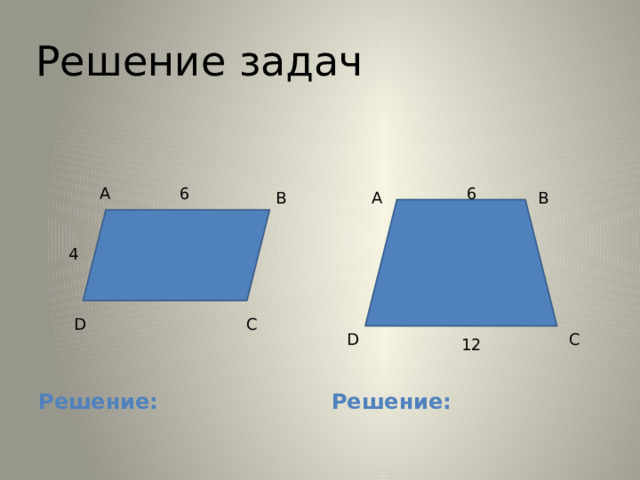
Решение задач

6

A

6

B

B

A

4

D

C

C

D

12

Решение:

Решение:

Самостоятельная работа

• . Найдите SINA, если COSA=-1/3 (COSA=-1/4)
• 2. Найдите COSA , если SINA= 2/5 (COSA=-2/3)
• 3. Проверьте, лежат ли на единичной окружности точки:
• В(7;3),С(0,5;0,5) (С(2;3), В(-0,5;0,5))
• 4. Угол между лучом ОМ, пересекающим единичную полуокружность, и положительной полуосью Ох равен А. Найдите координаты точки М, если ОМ=8,(ОМ=10) А=30 (А=60

)

Домашнее задание

• П. 96 (доказательство теоремы)
• № 1020 (б, в ) , 1021, 1022