Билет №1.
1. Сформулируйте определение выпуклого многоугольника ( периметр, диагональ). Сформулируйте теорему о сумме углов выпуклого многоугольника.
2. Признаки подобия треугольников. Доказать один признак на выбор обучающегося.
3. В окружность вписан треугольник ABC так, что АВ - диаметр окружности. Найдите углы треугольника, если: дуга ВС=134°;
Билет №2.
1. Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
2. Площадь прямоугольника (формулировка и доказательство).
3. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника
Билет №3
1. Параллелограмм. Определение. Свойства.
2. Теорема об окружности, вписанной в треугольник.
3. Стороны прямоугольника равны 3 см и
Билет № 4.
1. Четырехугольник. Сумма углов четырёхугольника.
2. Свойство касательной к окружности (формулировка и доказательство).
3. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Билет № 5.
1. Свойства площадей.
2. Теорема о средней линии треугольника (формулировка и доказательство).
3. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см. считая от основания. Найдите периметр треугольника.
Билет № 6
1. Трапеция. Определение. Виды трапеций. Свойство равнобедренной трапеции.
2. Свойство отрезков касательных, проведенных из одной точки (формулировка и доказательство).
3. Подобны ли треугольники ABC и МКР если:
АВ=3 см, ВС=5 см, СА=7 см, МК=4, 5 см, КР=7, 5 см, РМ = 10, 5 см.
Билет № 7
1. Прямоугольник. Свойства прямоугольника. Квадрат.
2. Теорема о вписанном угле (формулировка и доказательство).
3. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите: АВ, если ОВ=4 см, OD=10 см, DC=25 см.
Билет № 8
1. Ромб. Свойства ромба. Квадрат.
2. Свойство биссектрисы угла (формулировка и доказательство).
3. Площади двух подобных треугольников равны 75 и 300. Одна из сторон второго треугольника равна 9. Найдите сходственную ей сторону первого треугольника.
Билет № 9
1. Квадрат. Свойства квадрата.
2. Свойство серединного перпендикуляра к отрезку (доказательство).
3. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.
Билет № 10.
1. Подобные треугольники. Определение. Коэффициент подобия.
2. Свойства прямоугольника.
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см. а больший угол равен 135°.
Билет № 11.
1. Медиана треугольника. Определение. Свойство точки пересечения медиан треугольника.
2. Площадь параллелограмма (формулировка и доказательство).
3. Две стороны треугольника равны 7, 5 см и 3, 2 см. Высота, проведенная к большей стороне, равна 2, 4 см. Найдите высоту, проведенную к меньшей из данных сторон.
Билет № 12.
1. Пропорциональные отрезки в прямоугольном треугольнике.
2. Теорема об окружности, описанной около треугольника (формулировка и доказательство).
3. Найдите площадь прямоугольника, если одна из его сторон равна 5 см, а угол между диагоналями равен
Билет № 13.
1. Свойство описанного четырехугольника.
2. Свойства ромба (формулировка и доказательство).
3. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.
Билет № 14.
1. Свойство вписанного четырехугольника.
2. Площадь треугольника (формулировка и доказательство).
3. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Билет № 15.
1. Центральный угол. Вписанный угол.
2. Площадь трапеции (формулировка и доказательство).
3. Найдите площадь равнобедренного треугольника, если его основание равно 10см, а боковая сторона
равна 13см.
Билет № 16.
1. Значения синуса, косинуса и тангенса для углов 30° , 45° , 60° .
2. Теорема, обратная теореме Пифагора (формулировка и доказательство).
3. Катеты прямоугольного треугольника равны 6 и 8см. , гипотенуза 10 см. Вычислите высоту, проведённую к гипотенузе.
Билет № 17
1. Описанная окружность. Центр окружности, описанной около треугольника.
2. Свойства параллелограмма (формулировка и доказательство).
3. Найдите площадь трапеции с основаниями AD и BC, если АD=12см, ВС=6см, СD=5см, АС=13см.
Билет № 18
1. Вписанная окружность. Центр окружности, вписанной в треугольник.
2. Теорема Пифагора (формулировка и доказательство). Пифагоровы треугольники.
3. Найдите площадь параллелограмма, если АD =12см, ВD=5см, АВ=13см.

 Получите свидетельство
Получите свидетельство Вход
Вход


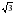 см. Найдите углы, которые образует диагональ со сторонами прямоугольника.
см. Найдите углы, которые образует диагональ со сторонами прямоугольника.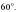
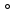 , 45
, 45








 Билеты к устному экзамену по геометрии (8 класс) (21.82 КB)
Билеты к устному экзамену по геометрии (8 класс) (21.82 КB)
 5
5 32778
32778 1951
1951



Скиньте ответы в вк пожалуйста 4ejiobe4elc
Скинь ответы плз,если есть
скиньте ответы на почту. пожалуйста