МБОУ СШ № 47 г. Красноярск
ФИО учителя: Лавенкова Любовь Серафимовна
Класс: 11 А
УМК:
1. Алгебра и начала анализа. 11 кл. : учеб. для общеобразоват. учреждений / Г. К. Муравин, О. В. Муравина. — 5-е изд., ст. — М. : Дрофа, 2018
2. Алгебра и начала анализа. 11 кл.: метод, пособие к учеб. Г. К. Муравина, О. В. Муравиной «Алгебра и начала анализа. 11 класс» / Г. К. Муравин, О. В. Муравина.М. : Дрофа, 2017
Предмет: математика
Тема: «Площадь криволинейной трапеции»
Тип урока: урок ознакомления с новым материалом.
Место и роль урока в изучаемой теме: первый урок по теме, вводятся основные определения «криволинейная трапеция», «интеграл».
Цели урока:
формирование понятий криволинейной трапеции и интеграла:
сформулировать умение записывать площадь криволинейной трапеции через сумму и разность интегралов.
Предметные результаты обучения:- формулировать определения криволинейной трапеции, интеграла, интегрирования;
записывать площадь изображённой плоской фигуры с помощью интеграла, суммы или разности интегралов
умение переводить язык математических формул на графический и обратно;
применять знания по геометрии для вывода формул площади.
материал вводится на наглядно-интуитивном уровне, поэтому использование презентации позволяет сделать объяснение более наглядным, а урок проходит интенсивнее.
Оборудование – компьютер, экран
Наглядность - презентация.
| № | Этап урока | Деятельность учителя | наглядность | деятельность уч-ся |
| 1. | Организационный момент | Сформулировать тему и цели урока. |
|
|
| 2. | Изучение нового материала (криволинейная трапеция) (5 мин.) | Ввести понятие криволинейной трапеции. Рассмотрим фигуру, изображенную на рисунке, изображение и определение записываем в тетрадь.
| Слайд №1 | Рисунок и определение криволинейной трапеции в тетрадь |
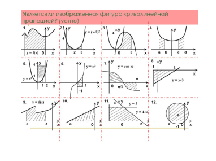
| 2.1 | Работа с определением криволинейной трапеции (5 мин.) | Объясняет алгоритм выполнения задания: 1. выделяем график функции, непрерывной и не меняющей знак на отрезке [a;b] 2. точки с абсциссам х=а, х=в, 3. делаем вывод: является ли фигура криволинейной трапецией. Объясняет отличие криволинейной трапеции от плоской фигуры. Обращает внимание на то, что плоскую фигуру можно представить как разность или сумму криволинейных трапеций. | Слайд №2 | Устная работа. Учащиеся отвечают и обосновывают свой ответ, опираясь на определение криволинейной трапеции. |
|
3. |
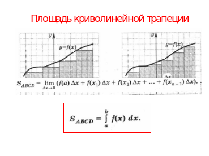
Изучение нового материала (площадь криволинейной трапеции и интеграл) (7 мин.) | Вводит понятие площади криволинейной трапеции и интеграла. Организует обсуждение : 1. как можно найти площадь криволинейной трапеции (разбиение фигуры на прямоугольники) 2. как более точно вычислить площадь (уменьшать х) 3. как записать площадь через предел. Проговаривает определение интеграла, записывает площадь трапеции через интеграл | Слайд №3 | Устная беседа. Записывают формулу площади криволинейной трапеции через интеграл в тетрадь. |
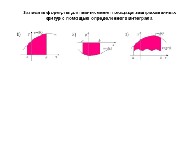
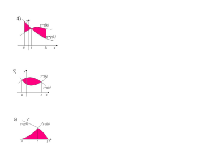
| 3.1 | Работа с ведением понятия площади криволинейной трапеции и интеграл ( 8 мин) | Ученикам раздаются листы с рисунками плоских фигур на плоскости (листы остаются у учеников как конспекты). Для каждого типа фигуры проговаривает правило записи площади через интеграл, сумму или разность интегралов, правило симметрии. Записывает на доске под каждой фигурой площадь с помощью интеграла. | Слайды № 4,5 | Записывают за учителем на листах под каждой фигурой площадь с помощью интеграла. |
|
4. |
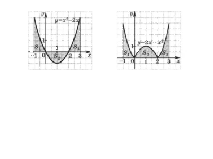
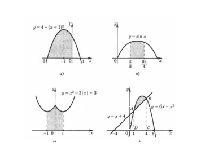
Закрепление нового материала (запись площадей плоских фигур с помощью интегралов) (12 мин) | 1. Рассмотрим на примере задачи №1 учебника стр. нахождение площади криволинейной трапеции. 2. упр. № 179 ученики решают самостоятельно, затем проверяем (записывают ученики на доске) 3. дополнительное задание №182 (г) | Слайд №6
Слайд № 7
Слайд № 8
| 1. Ученики самостоятельно изучают пример № Обсуждают решение. 2. решают упр. № 179 самостоятельно с последующей проверкой на экране 3. те, кто раньше выполнили задание, решают № 182 (г) |
|
5. |
Итог урока (рефлексия, оценивание работы учащихся) (3 мин) | Фронтальная работа Какая фигура называется криволинейной трапецией? Как найти площадь криволинейной трапеции? Как найти площадь плоской фигуры? Оценки прокомментировать. Оценка работы всего класса.
|
| Ответы устно, можно использовать при ответе записи в тетради |
| 6 | Домашнее задание (1 мин) | № 183 Повторить графики элементарных функций. |
| Записывают д.з
Задают вопросы.
|
Приложение (слайды) (№ 1-7)
слайд № 1
 слайд № 2
слайд № 2
слайд № 3
слайд № 4
слайд № 5
слайд № 6
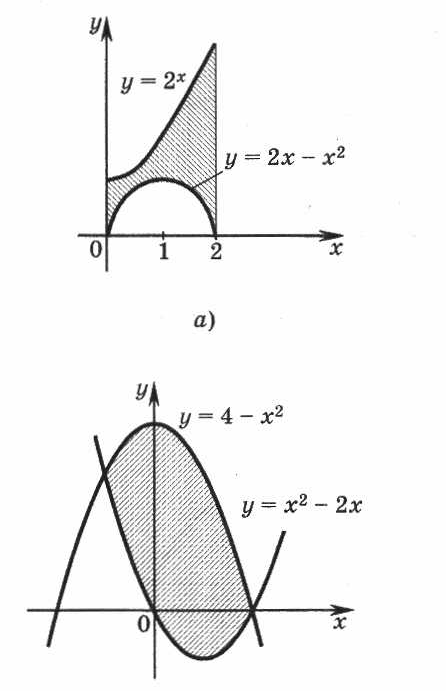
слайд № 7
слайд № 8
Самоанализ урока математики
МБОУ СШ № 47 г. Красноярск
ФИО учителя: Лавенкова Любовь Серафимовна
Класс: 11 А
Тема: «Площадь криволинейной трапеции»
Тип урока: урок ознакомления с новым материалом.
Место и роль урока в изучаемой теме: первый урок по теме, вводятся основные определения «криволинейная трапеция», «интеграл».
Цели урока:
формирование понятий криволинейной трапеции и интеграла:
сформулировать умение записывать площадь криволинейной трапеции через сумму и разность интегралов.
При планировании урока были учтены возрастные и психологические особенности класса (стремление работать индивидуально), способность большинства учащихся к самоорганизации.
Выбор структуры и типа урока обосновывался местом урока в теме (1-й урок), содержанием урока в соответствии с требованием учебной программы. Для проведения урока я заранее подобрала необходимый теоретический материал. Материал вводится на наглядно-интуитивном уровне, поэтому мною была подготовлена презентация, что позволило сделать объяснение более наглядным, а урок более интенсивным и продуктивным.
На уроке были созданы условия доброжелательного сотрудничества, для предупреждения утомляемости применялись смена видов деятельности, наглядность, работа с различным учебным материалом.
Основной задачей урока являлось дать учащимся конкретные определения новых математических понятий, организовать закрепление нового учебного материала для дальнейшего успешного изучения темы.
Структура урока согласована с типом и целями урока и представлена следующими этапами:
1) организационный момент (1 мин.);
2) изучение нового материала (определение трапеции), с последующим закреплением (8 мин.);
3) изучение нового материала (площадь), с последующим закреплением (10 мин.);
4) закрепление нового материала, решение упражнений (15 мин.);
5) итог урока (рефлексия) (5 мин.);
6) домашнее задание (1 мин.).
Время было выбрано с учетом объема изучаемого материала. Все запланированные этапы урока были проведены четко, последовательно с соблюдением временных рамок. Структура урока соответствовала целям и его содержанию. Весь используемый на уроке теоретический материал полностью соответствовал теме урока и был необходим ученикам для выполнения заданий.
Я не дифференцировала работу учащихся, т.к. материал урока носит первичный характер и необходим всем учащимся, все задания были базового уровня подготовки. На уроке была создана атмосфера взаимопомощи, все ученики могли общаться между собой, помогать друг другу. Ученики были сосредоточены, внимательны, дисциплина не нарушалась.
Организационный момент включал в себя приветствие учителем учащихся, проверку готовности кабинета и учащихся к уроку, объявление темы и целей.
Введение нового учебного материала было разбито на два блока: 1) определение криволинейной трапеции; 2) площадь криволинейной трапеции. В начале каждого блока мною вводились определения и давались необходимые разъяснения, затем эти понятия отрабатывались учащимися при выполнении заданий (устно и письменно) под моим вниманием. Учащиеся проявили активность и понимание изучаемого материала.
На этапе закрепления новых знаний учащиеся самостоятельно выполнили упражнение, записали формулы площади для произвольных фигур. Учащиеся активно обсуждали, доказывали правильность своего решения.
При подведении итогов урока учащиеся продемонстрировали понимание материала, его усвоение, способность применить на практике новые знания и использовать их для дальнейшего изучения темы. Это значит, что цели и задачи урока были достигнуты.
Содержание урока придерживалось и точки зрения обще-дидактических принципов:
принцип научности (содержание материала соответствовало уровню современной науки);
принцип доступности (учитывались возрастные особенности учащихся, выполнялись условия: следовать от простого к сложному, от неизвестного к известному);
принцип прочности знаний (созданы условия для запоминания: повторение изученного материала, создание ситуаций, вызывающих активную умственную работу над ними);
принцип последовательности (логическая стройность излагаемого материала, отсутствие пропусков в изложении).
Урок был построен методически грамотно: наличие четкой структуры, реализация каждого этапа соответствующими методами, учет дидактических принципов и целей математического образования. Я осуществляла обратную связь, речь была достаточно грамотной, не содержала неизвестных терминов. Весь использованный на уроке материал и задачи полностью соответствовали программе и уровню подготовленности учеников. Материал на уроке излагался доступным и грамотным языком. Взаимоотношения учителя и учащихся на протяжении всего урока носили характер сотрудничества. Ученики внимательно слушали, активно отвечали на вопросы, выполняли задания.
На мой взгляд, поставленные задачи и цели урока были достигнуты. Во время урока удалось выполнить весь запланированный объем работы.
Учитель математики Лавенкова Л.С.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Площадь криволинейной трапеции (5.43 MB)
Площадь криволинейной трапеции (5.43 MB)
 0
0 214
214 5
5 Нравится
0
Нравится
0


