ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИАНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
МОСКОВСКОЙ ОБЛАСТИ
СОЦИЛЬНО-ТЕХНОЛОГИЧЕСКИЙ ТЕХНИКУМ
Г. ОРЕХОВО-ЗУЕВО
Методическая разработка урока
на тему:
«Первообразная и площадь криволинейной трапеции ».
Рассмотрено на заседании
цикловой комиссии
общеобразовательных дисциплин
Председатель ц/к:
Преподаватель: Новикова Т.Ю.
2014 – 2015 гг.
Тема: ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ.
Тема урока: Первообразная и площадь криволинейной трапеции.
Цели урока:
Образовательные:
повторить правила нахождения первообразной,
повторить основные свойства первообразной,
повторить основные формулы,
повторить правило нахождения площади криволинейной трапеции;
рассмотреть различные способы нахождения площади криволинейной трапеции и сделать выбор наиболее точного из них;
проверить степень усвоения данной темы;
обобщить полученные знания по данной теме.
Развивающие:
содействовать формированию умений самостоятельно осуществлять контроль за выполнением операций в работе,
самостоятельно работать при выполнении заданий,
содействовать развитию логического мышления.
Воспитывающие:
содействовать формированию положительных мотиваций в отношении к работе, умению работать в коллективе,
содействовать воспитанию трудолюбия, активности, аккуратности в работе.
Учебно-материальное оснащение:
презентация,
наглядные пособия.
Педагогические технологии:
ИКТ;
Групповая технология;
Проблемное обучение.
ПЛАН УРОКА
Организационная часть
Принять рапорт от старосты, проверить присутствующих.
Проверить готовность к занятию.
Назначить дежурных.
Введение в учебную деятельность
Довести до сведения учащихся тему урока. Провести целевую установку с использованием демонстрационного материала, т.е. сформировать мотивацию, установить связи между учителем и учащимися. Сообщить учащимся план-задание на день.
Актуализация знаний и умений
Вопросы для актуализации:
Дайте определение первообразной?
Озвучьте основные свойства первообразной?
Чему равна первообразная функции xn?
Скажите, что означает С в записи первообразной?
Как называется вид первообразной, содержащий С?
Рассмотреть и повторить правило нахождения площади криволинейной трапеции.
Используя, какую формулу вы можете найти площадь криволинейной трапеции.
Ответ: S=F(b) – F(a).
Чем являются прямые x=b и x=a для криволинейной трапеции?
Ответ: Ограничивающими прямыми.
Каким неравенством они связаны?
Ответ: ba
Создание учебной ситуации
1.Теперь перейдем к решению примеров. Сначала вы разделитесь на 3 группы, каждая группа получит вот такую фигуру (приложение 2), площадь которой нужно будет найти тремя разными способами. У каждой группы будет свой способ решения. После работы в группах мы с вами сравним результаты и определим какой из способов наиболее точный.
Учащиеся делятся по группам.
Перед тем как приступить к работе, давайте все вместе посмотрим на листы, на которых изображена фигура и подумаем, как можно найти ее площадь.
Ответ: используя формулу для площади криволинейной трапеции
Да, можно и этим способом площадь этой фигуры будет находить первая группа. А еще как?
Ответ: можно разбить фигуру на геометрические фигуры, площади которых мы можем найти.
Да, это тоже одни из способов, вспомните, его мы с вами применяли, когда только начинали знакомиться с криволинейной трапецией. Этим способом площадь фигуры будет находить вторая группа.
Третья группа будет находить площадь фигуры, используя палетки, то есть наложением.
Итак, приступаем к работе, как только вы закончите мы посмотрим у кого сколько получилось и решим какой из способов наиболее точный.
Учащиеся работают в группах, учитель контролирует процесс и отвечает на вопросы. Учитель на доске изображает две фигуры такие же как у учащихся на листках, которые в дальнейшем пригодятся для проверки результатом.
Вопросы учащихся.
Продолжим дальше.
Первая группа работала по формулу площади криволинейной трапеции.
Ответьте на мои вопросы:
Какими линиями ограничена фигура? (x=-1; x=2; y=x2)
Чему равна первообразная функции, ограничивающей фигуру? (x3/3)
Запишите на доске какие расчеты вы производили? (один ученик записывает решение и полученный результат)
Итак, у первой группы получилось 3.
Вторая группа искала площадь фигуру, используя разбиение на геометрические фигуры. Пожалуйста, выберите одного представителя от группы, который вот на этом чертеже покажет ваше разбиение и расскажет нам, как вы посчитали площадь.
Учащийся работает на доске.
Пока вторая группа оформляет свое решение, мы перейдем к третьей группе.
На клетчатой доске, которая похожа на палетку, изображена ваша фигура, используя чертеж расскажите как вы искали площадь. Вас я тоже попрошу выбрать одного представителя, который нам все и расскажет.
Ответ участника третьей группы.
Итак, ваша площадь равна приблизительно 3.
Мы уже увидели два результата, которые отличаются друг от друга, давайте посмотрим третий. ( возвращаемся к учащемуся второй группы и рассматривает его решение, которое он комментирует).
Итак, вот и последний результат. Давайте сравним все результаты и выберем наиболее точный, как вы думаете какой это результат?
Ответ: первой группы
Почему?
Ответ: фигура рассмотрена более точно, четче оформлены ее границы и исключены лишние части.
Еще раз посмотрите на наши способы решение, все они правильные, но одни дают более точный, а другие менее точный результат.
Скажите, когда удобно использовать первый способ?
Ответ: когда знаешь, какими линиями ограничена фигура
А второй способ?
Ответ: если можно разбить фигуру на геометрические фигуру, площадь которых можно найти без померь
И третий?
Ответ: если при наложении палетки четко видно, какое количество квадратиков занимает фигура.
Подведение итогов занятия
Сделать анализ степени достижения поставленных целей самими учащимися.
Выделить наиболее активных учащихся. Объяснить, почему?
Провести анализ допущенных ошибок (если таковые имеются) и пути их устранения.
Сообщить полученные оценки за урок.
Сообщить тему следующего урока.
Приложение 1
Презентация к уроку на диске может быть использована при проведении урока.
Приложение 2
Найдите площадь фигуры, изображенной на рисунке:
Приложение 3
Справочный материал.
| Функция | Первообразная |
| xn |  +C +C
|
| 
| lnx+C |
| 
|  +C +C
|
| sinx | |
| cosx | sinx+C |
| (kx+b)p, p≠-1, k≠0 | 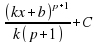
|
|  , k≠0 , k≠0
| 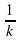 ln(kx+b)+C ln(kx+b)+C
|
|  , k≠0 , k≠0
|  +C +C
|
| sin(kx+b), k≠0 | -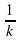 cos(kx+b)+C cos(kx+b)+C |
| cos(kx+b), k≠0 | 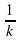 sin(kx+b)+C sin(kx+b)+C
|
Формула площади криволинейной трапеции: S=F(b) – F(a)
Литература:
Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений/ Ш. А. Акимов, Ю. М. Колягин, Ю. В. Сидоров и др. – 12-е изд. – М.: Просвещение, 2004. – 384с.
Алгебра и начала математического анализа. 11 класс. Самостоятельные работы для учащихся общеобразовательных учреждений/ Л.А. Александрова; под ред. А.Г. Мордковича. – 4-е изд., испр. и доп. – М.: Мнемозина, 2009. – 100с.
Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразовательных учреждений(базовый уровень)/ В.И.Глизбург; под ред. А.Г. Мордковича. – 4-е изд., испр. и доп. – М.: Мнемозина, 2009. –32с.
Контрольные и самостоятельные работы по алгебре и началам анализа: 11 класс: к учебнику А.Г. Мордковича и др. «Алгебра и начала анализа. 10-11 класс»/ М.А. Попов. – М.: Издательство «Экзамен», 2008. – 63с.
Предметная неделя математики в школе/ Т.Г. Власова. – Изд. 5-е – Ростов н/Д.: Феникс, 2009. – 168с.: - (Библиотека учителя).
ЕГЭ 2010. Математика: Сборник заданий/ В.В. Кочагин, М. Н. Кочагина. – М.: Эксмо, 2009. 208с. – (ЕГЭ. Сборник заданий).
Lib.Ru: Библиотека Максима Мошкова http://lib.ru/
Математика: учебник для учреждений нач. и сред. проф. образования/ М.И. Башмаков. - 6-е изд., стер. - М.: Издательский центр "Академия", 2012. - 256 с.
Математика. Задачник: учеб. пособие для учреждений нач. и сред. проф. образования/ М.И. Башмаков. - 2-е изд., стер. - М.: Издательский центр "Академия", 2013. - 416 с.


 Получите свидетельство
Получите свидетельство Вход
Вход



 +C
+C

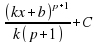
 , k≠0
, k≠0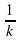 ln(kx+b)+C
ln(kx+b)+C , k≠0
, k≠0 +C
+C








 Методическая разработка урока математики "Первообразная и площадь криволинейной трапеции" (25.52 КB)
Методическая разработка урока математики "Первообразная и площадь криволинейной трапеции" (25.52 КB)
 0
0 839
839 117
117 Нравится
0
Нравится
0




