Министерство образования Республики Коми
Государственное профессиональное образовательное учреждение
Сыктывкарский лесопромышленный техникум
Учебное пособие
«Первообразная и интеграл»
Копецкая М.Г.
Преподаватель математики
высшей категории
Сыктывкар
2014год
Автор: Копецкая Марина Геннадьевна - преподаватель математики высшей квалификационной категории
Одобрено на заседании предметно - цикловой комиссии преподавателей естественнонаучного цикла
Рецензент: Елькина Зоя Ювенальевна – заместитель директора по ТО, Арцер Марина Николаевна – методист СЛТ
Учебно - методическое пособие разработано на основе технологии модульного обучения и содержит основные сведения, необходимые для организации и выполнения учебных действий обучающимися как на уроках, так и во внеаудиторное время.
Пособия поможет обучающимся самостоятельно (полностью или частично) обучаться по целевой индивидуализированной программе, что даст возможность для формирования совокупности “универсальных учебных действий”, обеспечивающих компетенцию “научить учиться”.
Учебное пособие может быть использовано преподавателями математики и обучающимися, которые изучают математику на базовом уровне.
Аннотация
Разработанное учебное пособие предназначено для обучающихся образовательных учреждений начального и среднего профессионального образования, изучающих математику на ступени основного общего образования, в частности для студентов ГПОУ Сыктывкарского лесопромышленного техникума, обучающихся по профессиям:
190631.01 Автомеханик; 250401.07 Машинист машин по производству бумаги и картона; 150709.02 Сварщик (электросварочные и газосварочные работы);
220703.02 Слесарь по контрольно-измерительным приборам и автоматике;
140446.03 Электромонтер по ремонту и обслуживанию электрооборудования
270802.10 Мастер отделочных строительных работ;
151013.01 Машинист лесозаготовительных и трелевочных машин.
Учебное пособие, разработанное на основе технологии модульного обучения, содействует развитию самостоятельности обучающихся, их умению работать с учетом индивидуальных способов проработки учебного материала, что повышает качество образования. В пособие реализуется системно - деятельностный подход, лежащий в основе Федерального государственного образовательного стандарта (ФГОС).
Цель учебного пособия – обеспечение поддержки учебного процесса по технологиям открытого образования. Учебное пособие может применяться для различных форм обучения (аудиторной и внеаудиторной). Также пособие предназначено для студентов, которые не имеют возможности прослушать весь курс в полном объеме (например, по состоянию здоровья).
Учебное пособие доступно в электронном виде, может распространяться на машинных носителях, например компакт - дисках (CD-ROM).
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к учебному пособию «Первообразная и интеграл»
Автор: преподаватель математики высшей квалификационной категории Копецкая Марина Геннадьевна
Целевое назначение
Учебное пособие предназначено для обучающихся, изучающих математику на базовом уровне, в частности для обучающихся образовательных учреждений начального и среднего профессионального образования.
Соответствие стандарту
По содержанию
В учебном пособие рассматривается тема «Первообразная и интеграл». Оно включает в себя материал, предусмотренный действующим государственным стандартом для обучения математике в старшей школе на базовом уровне. Содержание пособия распределено на 3 микромодуля:
М.М.1. Определение первообразной. Основное свойство первообразной. Правила нахождения первообразной.
М.М.2. Площадь криволинейной трапеции.
М.М.3. Понятие об интеграле. Формула Ньютона Лейбница.
По требованиям к уровню подготовки
Учебное пособие содержит достаточный практический материал для освоения основных предусмотренных стандартом умений и накопления опыта в использовании приобретенных знаний и умений в практической деятельности и повседневной жизни по данной теме. За основу взяты дидактические единицы из Примерной программы по математике для базового уровня автора Башмакова М.И.
По познавательным универсальным действиям
В соответствии с идеями стандартов нового поколения учебное пособие содержит достаточно материала для формирования стандартных универсальных действий, относящихся к поиску и выделению необходимой информации, структурированию знаний, выбору наиболее эффективных способов решения задач, осмыслению текста и рефлексии способов и условий действий.
Научно-методическая платформа
При разработке учебного пособия учитывалась реализация концепции продуктивного обучения, которая лежит в рамках общепринятого деятельностного подхода к обучению.
Особенности учебного пособия
В представляемом учебном пособии теоретическая часть представлена конкретной информацией по теме, а в практический блок включен материал, разбитый, как правило, на три уровня сложности.
Цели:
развитие у обучающихся способности к саморазвитию и самосовершенствованию;
формирование личностных ценностно-смысловых ориентиров и установок, личностных, регулятивных, познавательных, коммуникативных универсальных учебных действий;
повышение эффективности усвоения обучающимися знаний и учебных действий, формирования компетенций и компетентностей в предметных областях, учебно-исследовательской и проектной деятельности;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей.
Ожидаемый результат:
Внедрение учебного пособия «Первообразная и интеграл» в учебный процесс на практике позволит:
- сформировать общеучебные компетенции у обучающихся;
- повысить качество знаний по данной теме;
- использовать пособие во внеаудиторное время (электронный вариант);
- повысить самооценку обучающегося.
|
СОДЕРЖАНИЕ
| стр. |
Введение | 6-7 |
| 2. Учебное пособие «Первообразная и интеграл» 2.1. Информационный блок 2.1.1. М.М.1.Определение первообразной. Основное свойство первообразной. Правила нахождения первообразной 2.1.2. М.М.2. Площадь криволинейной трапеции 2.1.3. М.М.3. Понятие об интеграле. Формула Ньютона - Лейбница 2.2. Примеры решения задач 2.2.1. Примеры к модулю М. М.1. 2.2.2. Примеры к модулю М.М.2. 2.2.3. Примеры к модулю М.М.3. 2.3. Вопросы для самоконтроля 2.4. Творческие задания 2.5. Задачи для самостоятельного решения 3. Заключение 4. Используемые источники
|
9 -14
14 - 20
20 - 25
25 -26 26 |
1.Введение
Специфика современной системы образования состоит в том чтобы не только вооружать обучаемого знаниями, но и формировать у него потребность в самостоятельном овладении знаниями, творческом походе в овладении знаниями.
С введением Федеральных государственных образовательных стандартов профессионального образования нового поколения меняется подход к преподаванию дисциплин общеобразовательного цикла, который предусматривает формирование новых ключевых компетенций, необходимых для современного специалиста,
Модульная технология преобразует образовательный процесс так, что учащийся самостоятельно (полностью или частично) обучается по целевой индивидуализированной программе.
Содержание учебного материала пособия представлено в самостоятельных, законченных микромодулях с краткими конспектами теоретического материала с примерами, заданиями для самостоятельной работы и методическими рекомендациями к их выполнению Пособие соответствует определённой теме учебной программы. Задания, предлагаемые для самостоятельной работы разноуровневые: задания У –А (уровень обязательной подготовки); задания У – Б (типовые задания, решения которых состоит из нескольких действий); задания У – С («нестандартные задачи», требующие логических рассуждений).
Планирование уроков с применением учебного пособия, разработанного на основе технологии модульного обучения соответствует структурированию деятельности обучающегося в логике этапов усвоения знаний: восприятие, осмысление, запоминание, применение, обобщение, систематизация, контроль.
2.Учебное пособие: «Первообразная и интеграл»
2.1. Информационный блок
М.М.1. Определение первообразной. Основное свойство первообразной. Правила нахождения первообразной
Определение первообразной. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка
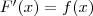
| Основное свойство первообразной. Задача интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные. При решении этой задачи важную роль играет следующее утверждение:
Признак постоянства функции. Если F'(х) = 0 на некотором промежутке I, то функция F — постоянная на этом промежутке.
Все первообразные функции f можно записать с помощью одной формулы, которую называют общим видом первообразных для функции f. Справедлива следующая теорема (основное свойство первообразных):
Теорема. Любая первообразная для функции f на промежутке I может быть записана в виде F(x)+C, где F (х) — одна из первообразных для функции f (x) на промежутке I, а С — произвольная постоянная.
Основному свойству первообразной можно придать геометрический смысл: графики любых двух первообразных для функции f получаются друг из друга параллельным переносом вдоль оси Оу (рис.). 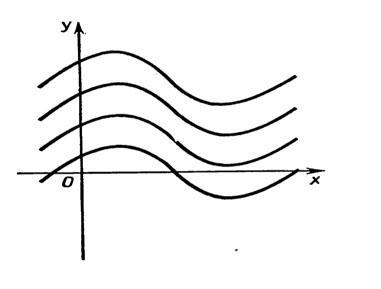
Таблица первообразных 
|
|
| |
|
|
|
Правила нахождения первообразных.
Правило 1 Если F есть первообразная для f, a G — первообразная для g, то F+G есть первообразная для f+g.
(F+G)'=F'+G'=f+g
| Правило 2.Если F есть первообразная для f, a k — постоянная, то функция kF — первообразная для kf.
(kF)'=kF'=kf. | Правило 3. Если F (х) есть первообразная для f (x), a k и b — постоянные, причем k≠0, то 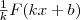 есть первообразная для f (kx+b). есть первообразная для f (kx+b). |
|
|
|
М.М.2. Площадь криволинейной трапеции.
Пусть на отрезке [а; b] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; b] и прямыми х = а и х = b (рис. 1), называют криволинейной трапецией.
Различные примеры криволинейных трапеций приведены на рисунках 1, а - д.
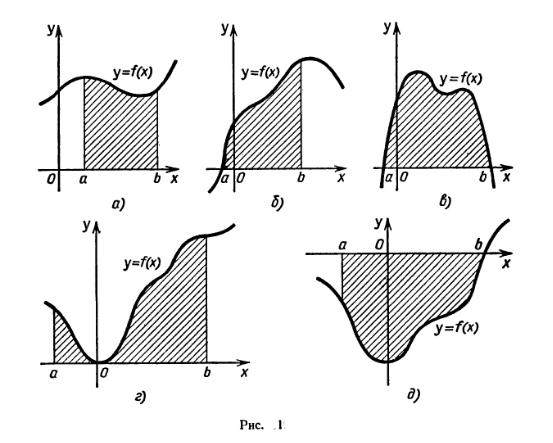
Для вычисления площадей криволинейных трапеций применяется следующая теорема:
Теорема. Если f — непрерывная и неотрицательная на отрезке [а; b]
функция, a F — ее первообразная на этом отрезке, то площадь S
соответствующей криволинейной трапеции) равна приращению
первообразной на отрезке [а; b] т. е.
S=F(b)-F(a).
М.М.3. Понятие об интеграле. Формула Ньютона - Лейбница
Рассмотрим другой подход к задаче вычисления площади криволинейной трапеции. Для простоты будем считать функцию f неотрицательной и непрерывной на отрезке [а; b] тогда площадь S соответствующей криволинейной трапеции можно приближенно подсчитать следующим образом.
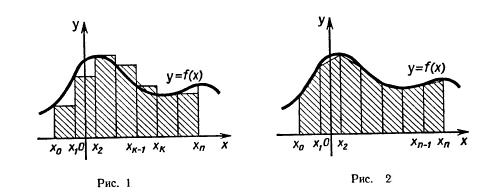
Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x0 = а1 2 n-1 n = b и пусть 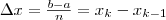 , где k = 1, 2, ..., n — 1, n. На каждом из отрезков [xk-1; xk] как на основании построим прямоугольник высотой F(xk-1). Площадь этого прямоугольника равна:
, где k = 1, 2, ..., n — 1, n. На каждом из отрезков [xk-1; xk] как на основании построим прямоугольник высотой F(xk-1). Площадь этого прямоугольника равна:
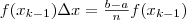
а сумма площадей всех таких прямоугольников (рис. 1) равна:
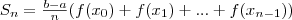
В силу непрерывности функции f объединение построенных прямоугольников при большом n, т. е. при малом Δx, «почти совпадает» с интересующей нас криволинейной трапецией. Поэтому возникает предположение, что Sn≈S при больших n. (Коротко говорят: «Sn стремится к S при n, стремящемся к бесконечности»— и пишут: Sn→S при n→∞.) Предположение это правильно. Более того, для любой непрерывной на отрезке [а; b] функции а (не обязательно неотрицательной) Sn при n→∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до b и обозначают 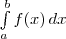 , т. е.
, т. е.
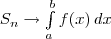 при n→∞ (1)
при n→∞ (1)
(читается: «Интеграл от а до b эф от икс дэ икс»). Числа а и b называются пределами интегрирования: а — нижним пределом, b — верхним. Знак 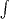 называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования. Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой
называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования. Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой
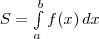
Формула Ньютона — Лейбница
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.
| Если 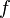 непрерывна на отрезке непрерывна на отрезке 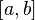 и F — её любая первообразная на этом отрезке, то имеет место равенство и F — её любая первообразная на этом отрезке, то имеет место равенство
|
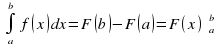
| 2.Примеры решения задач. 2.2.1. Пример 1. Найти первообразную для функции 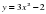 , проходящую через точку М(2;4). , проходящую через точку М(2;4). Решение. F(x =3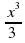 - 2х +с = - 2х +с =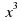 - 2х + с - 2х + с Получили, что множество всех первообразных задается семейством функций y=F(x)+C, то есть y=x3–2x+C, где С – произвольная постоянная. Зная, что первообразная проходит через точку М(2;4), подставим ее координаты в предыдущее выражение и найдем С. 4=23–22+С С=4–8+4; С=0. Ответ: F(x)=x3-2x – искомая первообразная 2.2.3. Пример 2. а) Вычислить интеграл 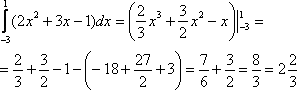 б) Вычислить интеграл 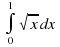 Решение: 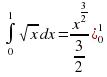 = =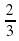 в) Вычислить интеграл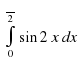 Решение: 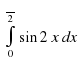 = - = - =- =- = 1 = 1
2.2.2. Пример3. Вычислите площадь фигуры, ограниченной линиями у=x3+1, у=0, x=0 Решение. F(x) =  +x; +x; S = F(0) - F(-1) = 0+0 - ( - (-1)) = - - (-1)) = - + 1 = + 1 =  Ответ:
Пример 4. Вычислите площадь фигуры, ограниченной линиями у=1+2sin x, у=0, x=0, x=п/2 Решение. F(x) = x - 2cosx; S = F(п/2) - F(0) = п/2 -2cosп/2 - (0 - 2cos0) = п/2 + 2 Ответ: п/2 + 2 квадратных единиц.
Пример 5. Вычислите площадь фигуры, ограниченной линиями у= 4 -х2, у=0, Решение. Сначала построим график, чтобы определить пределы интегрирования. Фигура состоит из двух одинаковых кусочков. Вычисляем площадь той части, что справа от оси у, и удваиваем. F(x) = 4x - x3/3; S = 2∙ (F(2) - F(0)) = 2∙(4∙2 -  -0)=16 - -0)=16 -  = 16 - 5 = 16 - 5  = 10 = 10 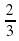 Ответ: 10 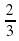 квадратных единиц. квадратных единиц.
Пример 6. Вычислите площадь фигуры, ограниченной линиями: у=1+ 0,5cos x, у=0, x=-п/2, x=п/2 Решение. F(x) = x+0,5sinx; S = 2∙(F( ) - F(0)) = 2∙( ) - F(0)) = 2∙( )+0,5∙sin( )+0,5∙sin( ) -0 - 0,5sin0 ) = 2∙( ) -0 - 0,5sin0 ) = 2∙( +0,5) = +0,5) = п +1≈ 4,14 Ответ: ≈ 4, 14 квадратных единиц. 2.2.3. Пример 7(М.М.3) Вычислить площадь фигуры, ограниченной линиями:  , ,  , ,  , ,  . . Решение: 1 Построить чертеж. При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые(если они есть) и только потом – параболы, гиперболы, графики других функций. Выполним чертеж (обратите внимание, что уравнение  задает задает
Штриховать криволинейную трапецию я не буду, здесь очевидно, о какой площади идет речь. На отрезке  график функции у = график функции у = расположен над осью расположен над осью  , , поэтому: Ответ:  2.3. Вопросы для самоконтроля: Сформулируйте определения первообразной. Сформулируйте основное свойство первообразной. Сформулируйте 3 правила нахождения первообразной. Какую фигуру называют криволинейной трапецией? Запишите формулу для вычисления площади криволинейной трапеции. Объясните что такое интеграл. Запишите формулу Ньютона – Лейбница. 2.4. Подготовить сообщения: Происхождение понятия определенного интеграла Подготовить презентацию по применению интеграла в жизни.
2.5. Задания для самостоятельной работы. При решении заданий студенты должны уметь: Доказывать, что функция F является первообразной для функции f, используя определение первообразной; находить первообразную в общем виде; находить первообразную, принимающую значение в заданной точке; вычислять интегралы; изображать криволинейную трапецию, ограниченную линиями, находить ее площадь
2.5. Задания для самостоятельной работы.
|
|
| |
|
|
|
1.Докажите, что функция F есть первообразная для функции f на промежутке(
F(х) = 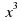 + 2х +1, f(х) = 3
+ 2х +1, f(х) = 3 + 2; (У-А)
+ 2; (У-А)
2). F(х) = 2 f(х) = 4
f(х) = 4 (У – Б)
(У – Б)
3) F(x)=х3-2х+1, f(x)=3х2-2 ; (У – А)
4) F(x)=2sin2х-2, f(x)=4cos2x; (У –Б)
5) F(x)=2 +1, f(x)=
+1, f(x)= ; (У –Б)
; (У –Б)
6) F(x)=х3-5х+12, f(x)=3х2-5); (У –А)
7) F(x)=2 cos 2х-4, f(x)=-4 sin2x; (У – Б)
8).F(x)=-2 +6, f(x)= -
+6, f(x)= - (У-Б)
(У-Б)
2.1 .Для функции f(х) = х2 найдите первообразную, график которой проходит через точку М( -1; 2) (У-А)
2.2 Для функции f(х) =  найдите первообразную, график которой проходит через точку А(
найдите первообразную, график которой проходит через точку А( (У –А)
(У –А)
2.3 Для функции f(х) = 2х +4 найдите первообразную, график которой проходит через точку В( (У – А)
(У – А)
2.4 Для функции f(х) =  найдите первообразную, график которой проходит через точку В
найдите первообразную, график которой проходит через точку В (У – А)
(У – А)
3. Найти первообразную для функции:
f(х) = 1; (У –А)
f(х) = х; (У –А)
f(х) = 5 + 2х + 2; ( У –А)
+ 2х + 2; ( У –А)
f(х) = 3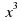 - 5
- 5 ; (У –А)
; (У –А)
f(х) =  ; (У – Б)
; (У – Б)
f(х) = 2 + 3
+ 3 (У –А)
(У –А)
f(х) =  + х2 на (0;
+ х2 на (0;  (У – Б)
(У – Б)
f(х) =  + х2; (У – Б)
+ х2; (У – Б)
f(х) = -
-  (У – Б)
(У – Б)
f(х) = (У – Б)
(У – Б)
f(х) =  ; (У – Б)
; (У – Б)
f(х) =  -
- (У –С)
(У –С)
f(х) =  (У –С)
(У –С)
4. Вычислите:
 ; (У –А)
; (У –А)
 (У –А)
(У –А)
; У –А)
 ; (У –А)
; (У –А)
(У –А)
(У –С)
 - 6х +9)
- 6х +9) (У –А)
(У –А)
 (У –А)
(У –А)
(У –А)
(У –С)
(У – Б)
(У – Б)
(У –С)
5.Найти площадь фигуры, ограниченной линиями:
 , у = 0, х= -3; (У –А)
, у = 0, х= -3; (У –А)
 (У –А)
(У –А)
у = 1 – х2, у = 0,  , у = 0; (У – Б)
, у = 0; (У – Б)
у = 9 – х2, х = 0, у = 0, х = -2; (У –А)
у = х2 + 1. х= -1 . х= 2, у = 0; (У –А)
 ; (У –А)
; (У –А)
 ; (У – Б)
; (У – Б)
 ,
,  .(У – Б)
.(У – Б)
у = -х2 + 2, у = - х; У –С)
у = х2- 2х +4 и у = 4; (У – Б)
у = - х2 + 4х, х = 0, х = 3, у = 0; (У – Б)
у = - х2 + 4, у = х2 -2х; У –С)
у = 1 – х2, у = - х – 1; (У – Б)
у = х2 – х – 5, у = х – 2; (У – Б)
.у = х2 – х - 4 , у = 6 – х2 ; У –С)
у = - х2 + 3х, у = 0;. у = - х2 +9; х = -2; х = 2; у =0; (У – Б)
у =25 – х2; х =-1; х = 3; у = 0; У –А)
у = 16 –х2; у = 0; У –А)
3. Заключение.
Рассматривая требования к результатам освоения основной профессиональной образовательной программы, можно сделать вывод, что все прописанные там компетенции удачно решаются с помощью технологии модульного обучения, то есть выпускник должен обладать общими компетенциями, включающими в себя способность:
ОК 2. Организовывать собственную деятельность, исходя из цели и способов ее достижения, определенных руководителем.
ОК 3. Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы.
ОК 4. Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в команде
4.Список используемых источников
Колмогоров А.Н. и др. Алгебра и начала анализа: Учебник для 10-11 классов общеобразовательных учреждений / А.Н.Колмогоров, А.Н.Абрамов, Ю.П. Дудницын. - М.: Просвещение, 2011г.- 384с
Ивлев Б.Н. Дидактические материалы по алгебре для 11 класса / Б.Н.Иевлев, С.М. Саакян, С.И. Шварцбурд. - М.: Просвещение, 2007г.-192с
Башмаков М.И. Математика: учебник для нач. и сред.проф.образования / М.И.Башмаков.- М.: Издательский центр «Академия», ОАО «Московские учебники», 2010.- 256с.
Башмаков М.И. Математика 11 класс. Сборник задач: среднее (полное) общее образование/ М.И.Башмаков. - М.: Издательский центр «Академия», 2010 – 208с

 Получите свидетельство
Получите свидетельство Вход
Вход






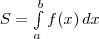
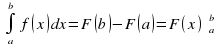
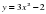 , проходящую через точку М(2;4).
, проходящую через точку М(2;4).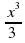 - 2х +с =
- 2х +с =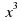 - 2х + с
- 2х + с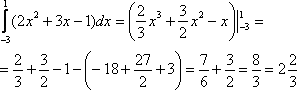
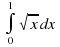
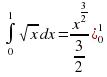 =
=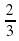
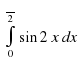










 Первообразная. Интеграл (0.34 MB)
Первообразная. Интеграл (0.34 MB)
 0
0 1685
1685 104
104 Нравится
0
Нравится
0






