Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b], называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
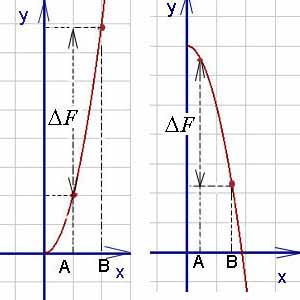
Как видно на графиках внизу (приращение первообразной функции обозначено), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) - F(a)).
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т. е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее - значение нижнего предела a и вычисляется разность F(b) - F(a). Полученное число и будет определённым интегралом.
Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход



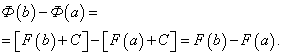
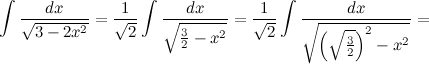









 Конспект урока по математике по теме «Понятие определённого интеграла» (74.29 КB)
Конспект урока по математике по теме «Понятие определённого интеграла» (74.29 КB)
 0
0 851
851 156
156 Нравится
0
Нравится
0


